本文是CUDA矩陣乘法系列文章的上篇。這個系列會從一個最簡單的實現出發，逐步優化到cuBLAS標準庫86%的性能，并詳細介紹其中涉及到的CUDA性能優化技巧。 本文首先給出了一個開箱即用的實驗源代碼，然后介紹了GPU硬件知識以及3種簡單實現，逐步展示了把性能從cuBLAS的0.39%優化到16%，即性能提升40倍的“魔法”。

本文首發于本人微信公眾號，原文鏈接：https://mp.weixin.qq.com/s/mh7pXnh6-SM6yqdGBGVm0Q

摘要

本文是CUDA矩陣乘法系列文章的上篇。

這個系列會從一個最簡單的實現出發，逐步優化到cuBLAS標準庫86%的性能，并詳細介紹其中涉及到的CUDA性能優化技巧。

本文首先給出了一個開箱即用的實驗源代碼，然后介紹了GPU硬件知識以及3種簡單實現，逐步展示了把性能從cuBLAS的0.39%優化到16%，即性能提升40倍的“魔法”。

寫在前面

矩陣乘法在當今的AI世界扮演著至關重要的角色，神經網絡的前向傳播，注意力機制的計算等最終都可以使用矩陣乘法來實現，一次大模型的推理背后是數以億計的矩陣乘法操作。因此，矩陣乘法的執行性能是一個需要重點關注的優化目標。

目前CUDA平臺上已經有很多高效的矩陣乘法的實現，例如cuBLAS，CUTLASS。

為了探究這些高效實現背后的原理，本文會從一個最簡單的矩陣乘法內核出發，通過逐步優化的方式來逐漸逼近cuBLAS的表現。

本系列文章會分為上下兩篇，上篇會介紹一下實驗環境，一些本系列會用到的GPU硬件知識，以及3種較為簡單的實現；下篇會繼續介紹剩下的4種更為復雜的實現。

參考資料

• 《How to Optimize a CUDA Matmul Kernel for cuBLAS-like Performance: a Worklog》，本文也是以這篇文章為主線展開的，文章鏈接 https://siboehm.com/articles/22/CUDA-MMM
• 《CUTLASS: Fast Linear Algebra in CUDA C++》，鏈接：https://developer.nvidia.com/blog/cutlass-linear-algebra-cuda/
• GodBolt：這是一個可以查看源代碼對應的匯編代碼的一個很好用的小工具，鏈接：https://godbolt.org/

實驗環境

實驗源代碼

本文實驗的源代碼已開源到了GitHub，鏈接：

https://github.com/QZero233/CudaMM

項目中包含了一個帶有正確性驗證的profiling工具，感興趣的朋友可以自行實現一些內核，然后使用這個工具來測試一下自己的實現的性能如何。

這個工具的運行結果如下圖所示，我們主要關注其中倒數第二行的以GFLOPS為單位的性能。

硬件環境

• 顯卡型號：NVIDIA GM107GL [Quadro K620]
• CUDA架構版本號：50
• CUDA版本：12.4
• NVCC版本：12

關于GPU你需要了解的那些事

從硬件視角看GPU

之前在CUDA并行規約那篇文章中提到過，在進行CUDA開發時，我們是以Grid，Block和Thread三級的層次結構來組織線程的，那么這三者是如何對應到具體的硬件實現的呢？

從硬件視角下看，一張顯卡里有一個GPU，GPU內部有多個流式多處理器（Streaming Multiprocessor，以下簡稱SM），如下圖所示：

接下來把視角轉向SM內部，每個SM有多個處理器，線程就是在這些處理器上具體執行的。

除此之外，每個SM還有一塊共享內存區域，之前文章里提到的共享內存（Shared Memory，以下簡稱SMEM）就是在這個區域，這個區域只能是SM內部的處理器訪問。SM內部的每個處理器又有著只能是自己訪問的寄存器（REGS）。

從這里也可以總結出GPU上內存訪問的速度排序，寄存器（REGS）是最快的，但是只能線程自身訪問；其次是SMEM，但是只能是Block內的線程訪問；最慢的是GMEM，GMEM就是我們通過cudaMalloc申請到的內存，所有線程均可訪問。

那么上述的線程層級架構又是怎么和這個硬件架構相對應的呢？ 而且Warp在其中又是怎么體現的呢？這就得從線程調度的角度來看一個內核被啟動的過程了。

在啟動內核時，我們會指定GridDim和BlockDim，這就使得內核有了一定數量的線程塊（Block）需要執行，每個Block里有若干個Thread。在進行調度時，GPU會以Block為單位，把一個Block分給一個SM，這時候一個SM可能會被分到多個Block。

接下來就是SM的工作了，一個Block里連續的32個線程為一個Warp，SM會以Warp為單位進行調度，即SM會選擇32個連續的線程，然后放到32個處理器上運行。上述過程如下圖所示。

全局內存訪問合并

同一個Warp里的線程有很多有意思的特性，對這些特性加以利用就能夠達成不錯的優化效果，全局內存訪問合并（Global Memory Coalescing）就是其中之一。

這個特性是：如果一個Warp里的線程訪問的內存恰好是連續的32個4B的浮點數，那么GPU就只會做一次長度為128B的訪存操作， 把128B的數據讀取之后分發給32個線程。這里參考資料作者的精美的手繪圖可以很形象地說明這一點：

一些約定

在開始正式實現前，首先需要把一些容易混淆的設定給明確了。

• 本文默認所有矩陣都是行優先存儲的
• 本文中的x都是指行下標，y都是指列下標

如下圖所示：

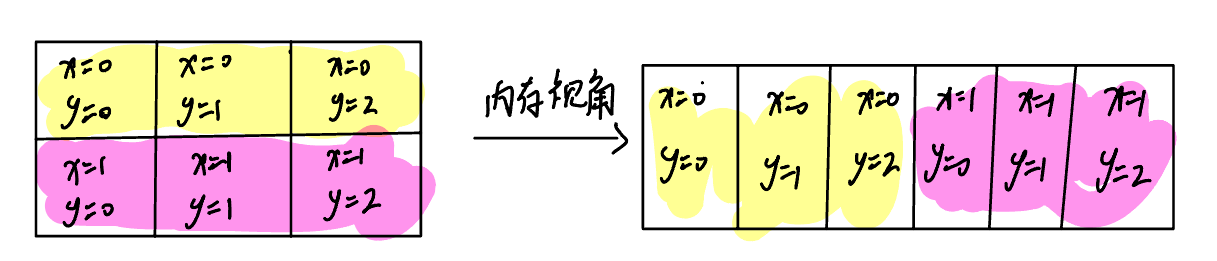
（注：本文所有的內核實現都只是在大小為4096的方陣下進行了正確性驗證，如果要適配任意形狀需要考慮很多corner case，這有點偏離主線了，所以本文就暫時不做這方面的適配工作了。）

V42：cuBLAS

這里先放出cuBLAS實現的性能數據，供后續比較和參考

V1：Naive Kernel

對于矩陣乘法\(C = A \times B\)，一個最樸素的想法就是讓每個線程都計算C中的一個元素，所以只需要一個Block，使用Thread的x和y表示要計算的C的元素坐標，然后2個for循環計算即可。

這個想法沒問題，只是在實現的時候，由于一個Block里面最多有1024個線程，所以需要進行一次分塊。

具體而言，可以把C分成若干個\(32 \times 32\)的塊（Tile），每個Tile交給一個Block進行計算，如下圖所示：

對于每個線程而言，首先需要根據計算出當前線程需要處理的C的坐標，然后用2個for循環計算結果并寫回即可。

至于布局，每個Block里自然是\(32 \times 32\)個線程，而Grid則是需要用向上取整的除法來分配盡量多的Block。

（注：理清楚每個線程需要計算哪些C的元素是不被后面更復雜的分塊繞暈的關鍵）

最終得到的源代碼如下所示：

__global__ void MatmulKernelV1(const scalar_t *a, const scalar_t *b, scalar_t *out, uint32_t M, uint32_t N, uint32_t P) {
    uint32_t x = blockIdx.x * blockDim.x + threadIdx.x;
    uint32_t y = blockIdx.y * blockDim.y + threadIdx.y;

    if (x < M && y < P) {
        scalar_t tmp = 0;
        for (uint32_t k = 0; k < N; k++) {
            // out[i][j] = a[i][k] * b[k][j]
            tmp += a[x * N + k] * b[k * P + y];
        }

        out[x * P + y] = tmp;
    }
}

void MatmulCoreV1(const scalar_t *a, const scalar_t *b, scalar_t *out, uint32_t M, uint32_t N, uint32_t P) {
    dim3 grid(std::ceil(M / 32.0), std::ceil(P / 32.0), 1);
    dim3 block(32, 32, 1);
    MatmulKernelV1<<<grid, block>>>(a, b, out, M, N, P);
}

實驗數據

最終的性能數據如下所示：

性能只有cuBLAS的0.39%，可以說是相當拉垮了。

理論分析

這里先插入一段理論分析，來分析一下Naive Kernel可能的性能瓶頸在哪。

首先計算一下理論最快的運行時間，進行一個4096方陣的乘法所需要浮點運算次數為\(2 \times 4096^3\)（因為C有\(4096^2\)個元素，每個元素需要進行4096次乘法和加法），大約為137GFLO；

而內存讀取最低需要\(2 \times 4096^2 \times 4\,\text{B}\)，約134MB，寫入需要\(4096^2 \times 4\,\text{B}\)，約67MB。

實驗用的顯卡浮點數計算性能為870GFLOPS，顯存帶寬為29GB/s，所以理論上計算最快需要157ms，訪存共需要6.9ms，也就是說，理論上來講，矩陣乘法應該是計算瓶頸的。

但是我們的Naive Kernel似乎并不是這樣的，下面來詳細分析一下。

在計算次數上，如果不考慮計算下標的開銷，那它的計算次數就是和理論最低值相等的；

在內存訪問上，實際上每個線程都會訪問\(2 \times 4096\)次全局內存（GMEM），如果這些訪問沒有經過任何優化，那么這個內核一共就會有

\(4096^2 \times 2 \times 4096 \times 4\,\text{B} = 549\,\text{GB}\)

的訪存，需要耗時18.9s，已經是計算的120倍了，所以很顯然，目前的首要任務是優化內存訪問。

（注：這里內存訪問事實上并沒有計算的那么多，因為有一些Warp層的自動優化，這個后面馬上會提到）

V2：Global Memory Coalescing

這里可以像防止Bank Conflict那樣，通過調整每個線程負責的區域來實現Coalescing。

我們首先分析一下V1里面每個線程都在計算C的哪一個元素。通過代碼可以知道，線程計算的C的x坐標就是threadIdx.x，y坐標就是threadIdx.y，并且threadIdx是x先變化的，所以第一個線程計算的是(0, 0)，第二個是(0, 1)，以此類推，如下圖所示（用背景色來區分T0和T1加載的數據）：

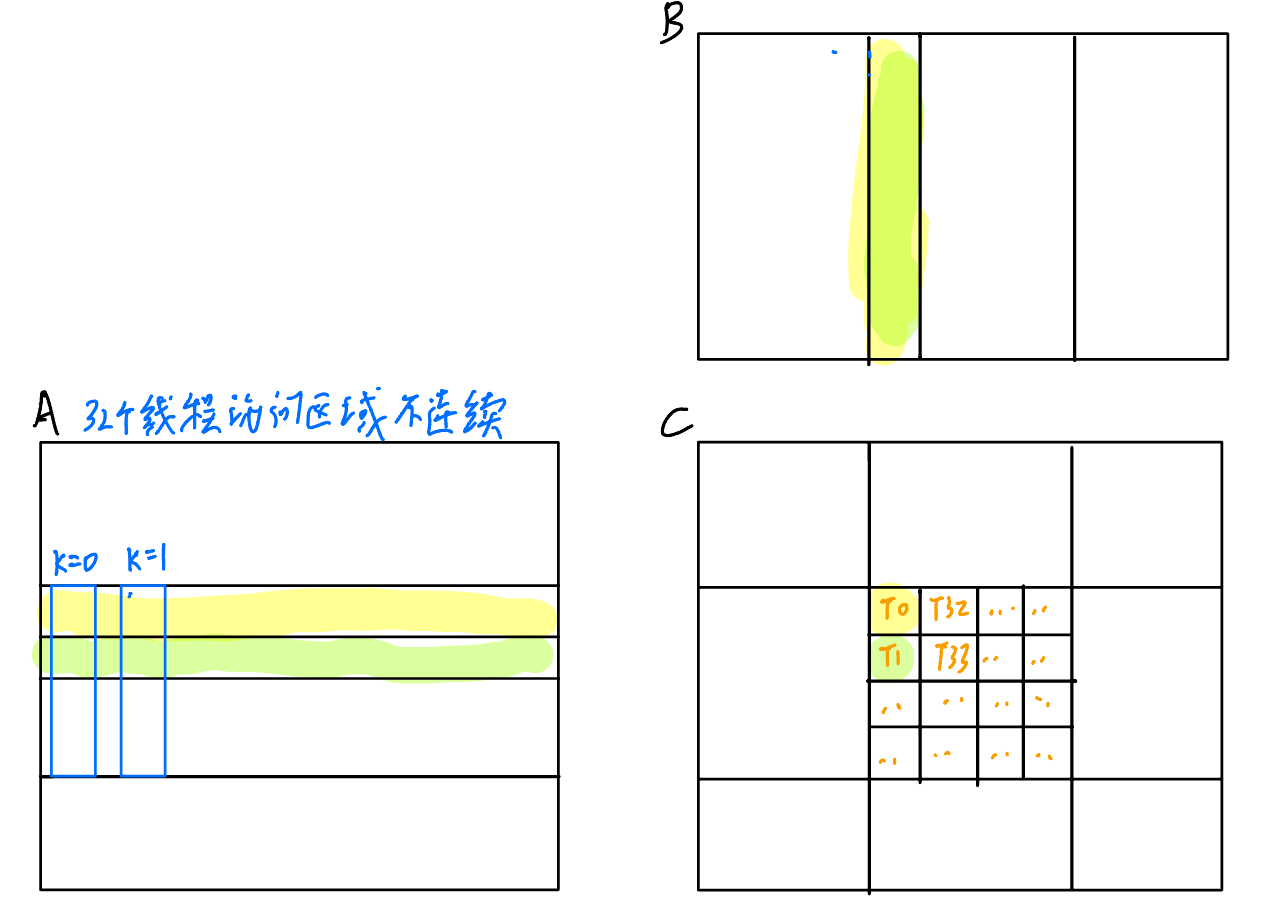
可以發現，一個Warp里計算的其實是C中的某一列，那么同一時刻，Warp里的線程訪問的A一定不是連續的，所以訪問A的部分一個Warp需要\(32 \times 4096\)次訪存，而訪問B的部分，由于一個Warp里的線程在同一時刻訪問的都是同一個B，所以這里只會有一次訪存開銷，那么訪問B總共就會有4096次訪存。

這里如果我們讓一個Warp計算C中的一行會怎么樣呢？那么訪問A就只需要4096次訪存，但是訪問B的時候，在同一時刻，線程們訪問的數據是連續的，此時就可以觸發Global Memory Coalescing，把32次訪存壓縮為1次，如下圖所示：

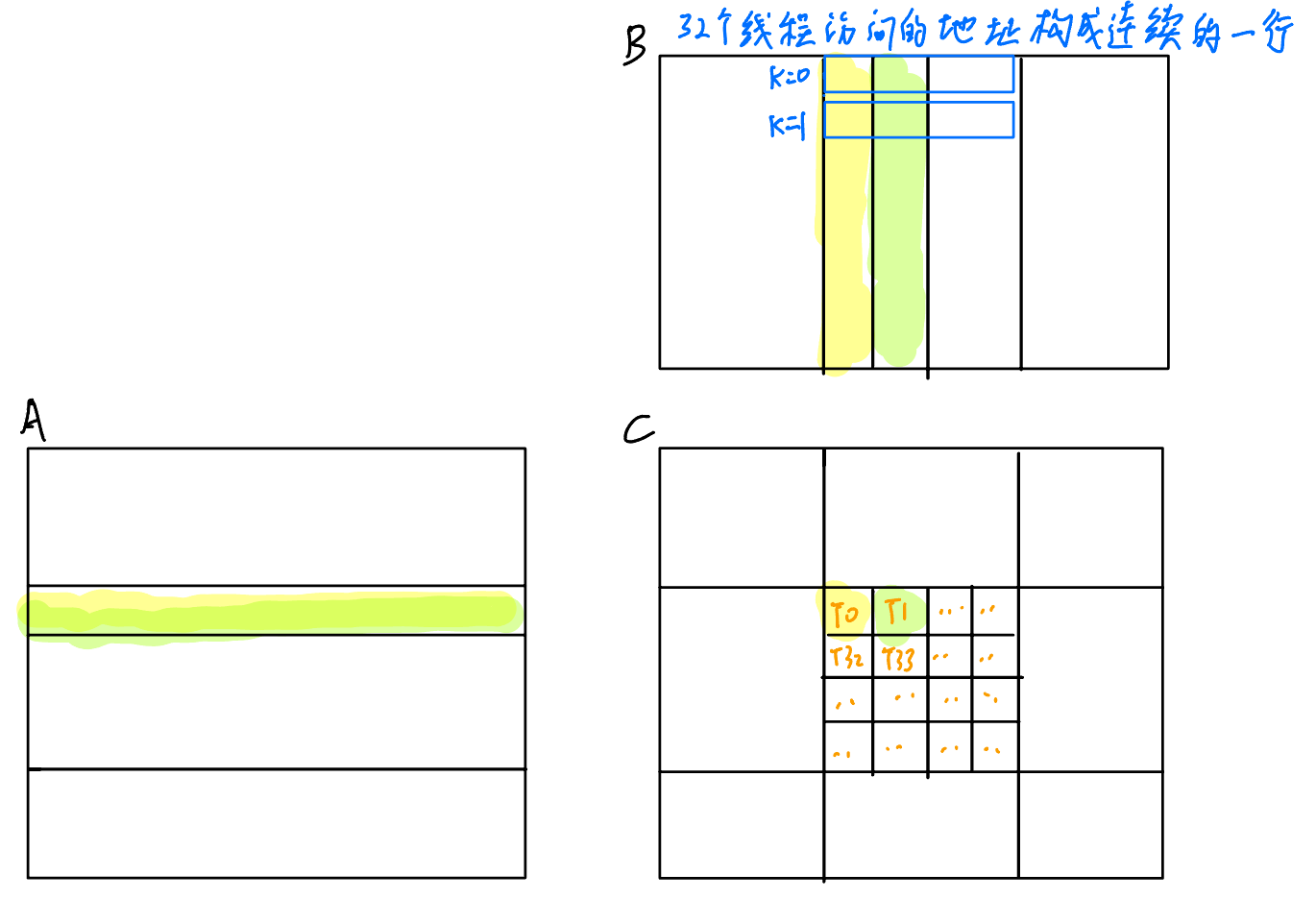
實驗數據

這里僅僅是對換一下x和y，性能就提升了接近8倍。

但是和cuBLAS相比，還是有不小的差距，目前也還只有cuBLAS性能的2%。

關于實現方式

具體實現時，只需要把x和y對換一下就行了。

參考資料作者在這里的實現是取消了threadIdx.y這個維度，然后把x維度的大小擴展為了1024，之后在線程內部根據threadIdx.x以及BlockSize來計算當前線程對應到C的坐標，如下所示：

constexpr uint32_t BLOCK_SIZE = 32;
__global__ void MatmulKernelV2(const scalar_t *a, const scalar_t *b, scalar_t *out, uint32_t M, uint32_t N, uint32_t P) {
    // 相當于首先把OUT分成若干個32*32的Block，V1和V2都是如此，它們的區別在于Block內部的分配方式
    // 這里blockIdx.x * BLOCK_SIZE, blockIdx.y * BLOCK_SIZE 就是在定位Block的起始x和y
    const uint32_t x = blockIdx.x * BLOCK_SIZE + threadIdx.x / BLOCK_SIZE;
    const uint32_t y = blockIdx.y * BLOCK_SIZE + threadIdx.x % BLOCK_SIZE;
......

個人認為這種實現肯定是不如直接對換x和y的，因為這種實現引入了除法和求余數這種非常昂貴的操作，但是實際測試下來兩種實現的性能是幾乎一致的。

于是我看了下兩種實現對應的PTX匯編，如下圖所示

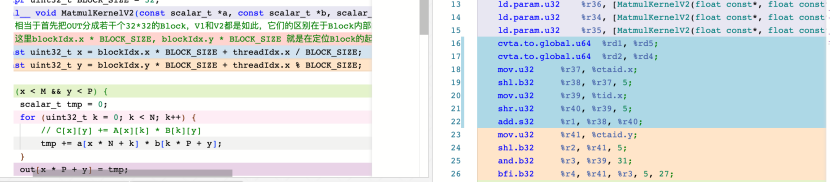
發現兩者指令數量幾乎都差不多，可能是因為這里BlockSize為2的整數次冪的關系吧，這種特性使得編譯器可以對求余數指令做優化，一般的求余數指令是需要用除法+減法來實現的。

如下圖所示，可以看到，在把BlockSize換成34之后，確實多出來了一條sub指令。

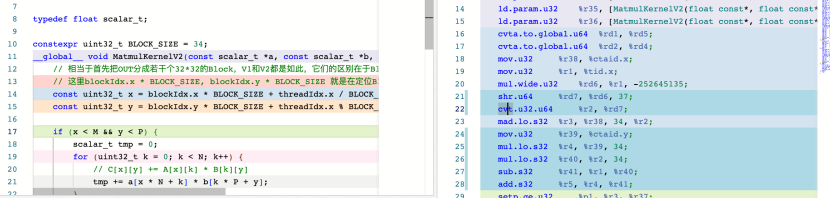
在把BlockSize改成31然后實際運行后，確實出現了性能的損失。

所以，有時候大小為2的整數倍確實能帶來一些額外的驚喜。

V3：Shared Memory Cache-Blocking

前文提到過，存儲訪問速度是REGS > SMEM > GMEM，最理想的情況是每個線程所需的所有數據都加載到REGS里，但是這顯然不現實；

那么退而求其次地，如果能把每個Block所需要的數據都加載到SMEM里，也能減少很多GMEM的訪問次數。

雖然一個線程所需計算C的大小是固定的，比如\(32 \times 32\)，C只需要A的32行和B的32列，但是A和B的形狀是不固定的，如果A的列很多，那也會擠爆SMEM。

這時候很自然的就能想到，如果我們用類似于滑動窗口的方法，每次加載固定大小的A和B到SMEM里，計算完成之后再繼續加載下一個窗口，并計算，這樣是否可行呢？

對于矩陣乘法這個操作而言，確實是可行的。我們以C中的某一個元素為例，如下圖所示：可以把A的對應行和B的對應列拆分為多個小塊W0，W1......，只需把對應的塊加載然后相乘之后累加，就能得到正確結果。

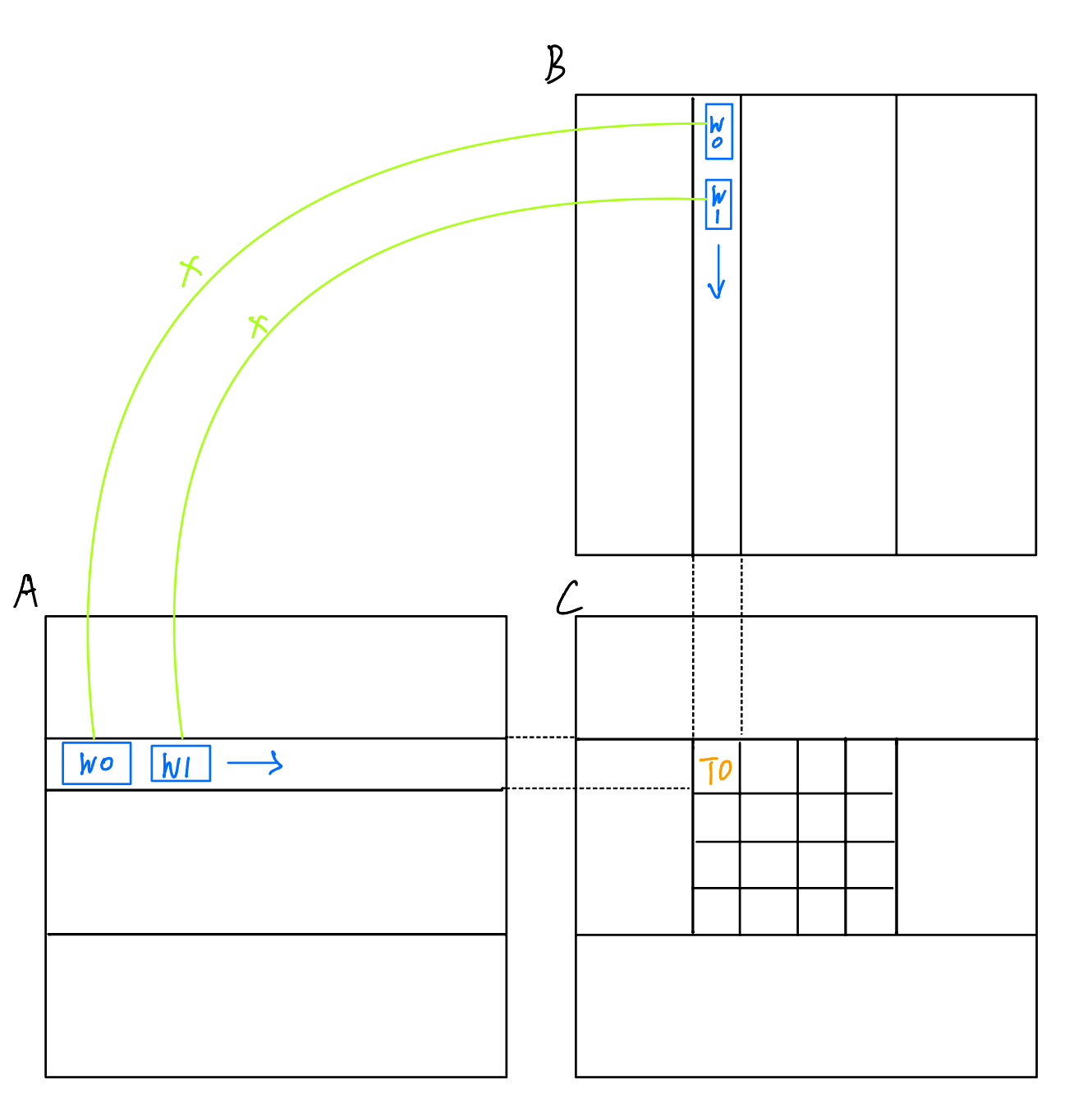
推廣到整個Block，我們就可以只加載所需行和列的部分數據到SMEM里，然后在SMEM里完成計算后再繼續加載，參考資料作者的圖可以很清晰地說明這一點：

具體實現

這里我們選取SMEM大小為\(32 \times 32\)，也就是剛好和線程數量相等，這樣在加載數據到SMEM階段，只需要每個線程加載一個元素即可，可以一一對應上。

從線程的視角來看，首先需要確認當前要計算的元素在C的坐標，然后還需要知道自己需要加載的元素的坐標，這里要加載的元素的坐標和線程在Block里的坐標是相同的，所以實現起來難度不大。
具體實現如下所示：

__global__ void MatmulKernelV3(const scalar_t *a, const scalar_t *b, scalar_t *out, uint32_t M, uint32_t N, uint32_t P) {
    __shared__ scalar_t As[BLOCK_SIZE * BLOCK_SIZE];
    __shared__ scalar_t Bs[BLOCK_SIZE * BLOCK_SIZE];

    const uint32_t x = blockIdx.x * BLOCK_SIZE + threadIdx.x / BLOCK_SIZE;
    const uint32_t y = blockIdx.y * BLOCK_SIZE + threadIdx.x % BLOCK_SIZE;

    if (x >= M || y >= P) {
        return;
    }

    // 記 threadX, threadY 為 (x, y) 在OUT塊中的位置
    // threadX = threadIdx.x / BLOCK_SIZE, threadY = threadIdx.x % BLOCK_SIZE
    uint32_t threadX = threadIdx.x / BLOCK_SIZE;
    uint32_t threadY = threadIdx.x % BLOCK_SIZE;

    scalar_t tmp = 0;
    for (int32_t k = 0; k < N; k += BLOCK_SIZE) {
        // 加載 A[x][k] - A[x + BLOCK_SIZE][k + BLOCK_SIZE] 到 As
        // 加載 B[k][y] - B[k + BLOCK_SIZE][y + BLOCK_SIZE] 到 Bs

        // 計算 SUM(As[threadX][:] * Bs[:][threadY]) 存儲到 OUT[x][y]
        As[threadX * BLOCK_SIZE + threadY] = a[x * N + (k + threadY)];
        Bs[threadX * BLOCK_SIZE + threadY] = b[(k + threadX) * P + y];

        __syncthreads();

        // 注意：這里在矩陣大小<32時會出問題，因為As實際上沒裝滿
        for (int32_t i = 0; i < BLOCK_SIZE; i++) {
            tmp += As[threadX * BLOCK_SIZE + i] * Bs[i * BLOCK_SIZE + threadY];
        }

        __syncthreads();
    }
    out[x * P + y] = tmp;

}

實驗數據

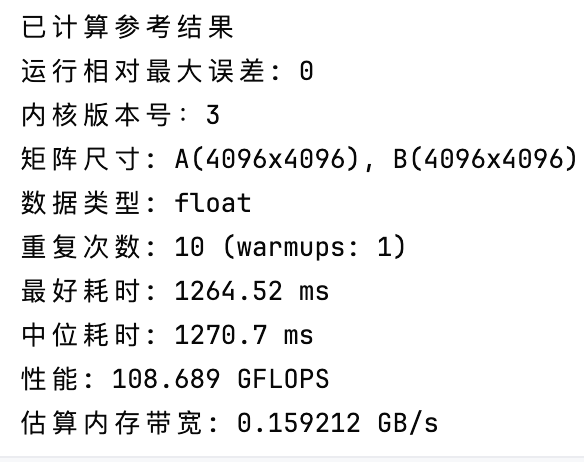
相較于V2，V3的性能直接提升了6倍多，此時的性能是cuBLAS的16%。

未完待續