P5322 [BJOI2019] 排兵布陣
我們瀏覽一遍測試點,發現了一個 \(s=1\) 的特殊性質。先考慮這一性質。
\(s=1\)特殊性質
如果我們當前第 \(i\) 座城市的兵力數量足夠時,添加兵力顯然不優。而如果兵力不夠,我們的最優策略挺顯然的,要么添加兵力使其恰好足夠,要么干脆就不要這個城市。
換句話說,我們對一個城市的決策只有選與不選兩種,選的話需要花費一定的體積,同時獲得一定的價值。
聽我這么一描述,是不是感覺這就是個很板的01背包?對的對的,這個部分分就是個01背包板子……忘記01背包的可以移步01背包基礎
而那個兵力限制 \(m\),往這個方向上考慮,其實就是個背包最大容量 \(V\)。
特殊性質代碼也貼在這里,希望有助于大家理解。
P5322特殊性質
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
int x=0,f=1;char c=getchar();
while(c<48){
if(c=='-') f=-1;
c=getchar();
}
while(c>47) x=(x<<1)+(x<<3)+(c^48),c=getchar();
return x*f;
}
const int N=120;
const int M=2e4+4;
int S,n,m,w[N],v[N],dp[M];
signed main(){
S=read(),n=read(),m=read();
int W=m;
//不同于我當時的博文,這里的w數組是代價,v數組是價值
for(int i=1;i<=n;i++){
int x=read();
//根據題意,第i座城市恰巧被占領的兵力是2*a[i]+1
w[i]=((x<<1)|1),v[i]=i;
}
//01背包模版
for(int i=1;i<=n;i++){
for(int j=W;j>=w[i];j--){
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
}
int ans=dp[m];
printf("%lld",ans);
return 0;
}
正解
那既然這個部分分是個背包dp,我們合理猜測本題也是個dp,搞不好還是背包dp。
考慮分組背包。簡單來說,既然對決是獨立的,我們對于某座城池,首先可以將 \(s\) 個人的駐守兵力從小到大排序。記排序后的數組為 \(b\)。
接下來的過程類似于你做題時拿部分分。
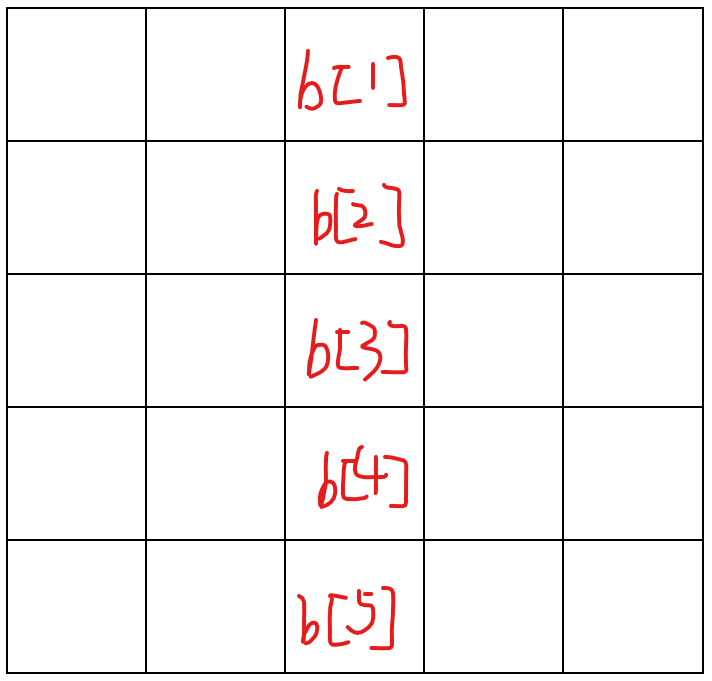
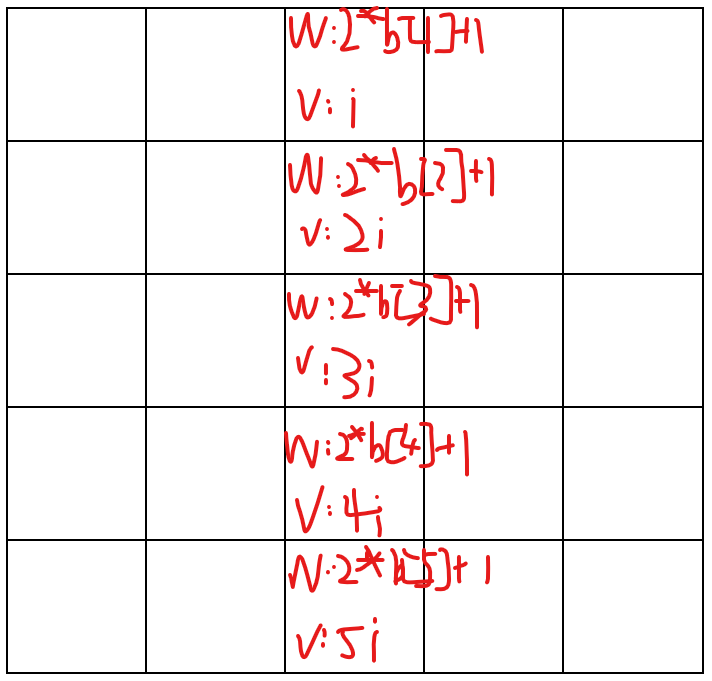
對于某個城市 \(i\),因為 \(b_1 \le b_2 \le \cdots b_s\) ,所以如果我們現在的駐扎兵力剛好可以拿下 \(b_j\) 的話,那它一定能且只能拿下 \(b_1,b_2,\cdots,b_j\)。
所以我們拆物品方法有所不同:對于\(i\) 城市兵力第 \(j\) 小的那個對應得物品,我們讓它的體積是 \(2*b_j+1\),價值是 \(j \times i\),如上圖所示。
(類似于你拿部分分,除非特殊性質,否則你拿到越靠后的分,用的時間一般越長,但拿到的分值也會越高。而且你能解決后面的部分分,也就能解決前面的部分分)
就像你做題的時候,一道題目只會有一個得分,對于 \(i\) 城市,貢獻只能有一個,所以這個分組背包的組就是每個城市,里面的物品就是剛才拆出來的 \(s\) 個。我們只能選擇一個物品的價值作為這個城市的最終貢獻。
總之分析到這里,本題就是個很板的背包dp,僅此而已。
代碼:
P5322
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
int x=0,f=1;char c=getchar();
while(c<48){
if(c=='-') f=-1;
c=getchar();
}
while(c>47) x=(x<<1)+(x<<3)+(c^48),c=getchar();
return x*f;
}
const int N=120;
const int M=2e4+4;
int S,n,m,w[N],v[N],dp[M],a[N][N],b[N],W[N][N],V[N][N],DP[N][M];
signed main(){
S=read(),n=read(),m=read();
for(int i=1;i<=S;i++){
for(int j=1;j<=n;j++){
a[i][j]=read();
}
}
//拆分物品
for(int i=1;i<=n;i++){
for(int j=1;j<=S;j++){
b[j]=a[j][i];
}
sort(b+1,b+S+1);
for(int j=1;j<=S;j++){
W[i][j]=2*b[j]+1,V[i][j]=i*j;
}
}
//分組背包
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
for(int k=0;k<=S;k++){
//k=0時的物品價值是0,代價是0,相當于根本不要i城市的情況
if(j>=W[i][k]){
DP[i][j]=max(DP[i][j],DP[i-1][j-W[i][k]]+V[i][k]);
}
}
}
}
int ans=DP[n][m];
printf("%lld",ans);
return 0;
}



 浙公網安備 33010602011771號
浙公網安備 33010602011771號