并查集學習
模板
class DisjointSet {
public:
int count = 0;
vector<int> parent;
DisjointSet(int n) {
this->count = n;
parent = vector<int>(n);
for (int i = 0; i < n; i++) parent[i] = i;
}
int find(int p) {
while (p != parent[p]) {
parent[p] = find(parent[p]);
// parent[p] = parent[parent[p]];
p = parent[p];
}
return p;
}
void unions(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
parent[rootP] = rootQ;
--count;
}
};
- 解決分群、分類別的問題
題目列表
- LC.547.朋友圈
- LC.200.島嶼數量
- LC.130.被圍繞的區域
- LC.685.冗余連接II(困難)
- LC.684.冗余連接
LC.200.島嶼數量
- 除了搜索遞歸回溯的方法,此題也適用于并查集
- 簡單思路:對所有陸地為1的塊進行如上面模板一樣的parent[i]=i操作,此處是parent[im+j]=im+j,其中i是行號,j是列號,m是行長度;為0的則輸入-1占位,然后再一次遍歷,此時只需要判斷某位置的下方和右方是否有為1的陸地然后做union操作即可
class DisjointSet {
public:
int count;
DisjointSet() {
count= 0;
}
void insert(int i) {
parent.push_back(i);
if (i != -1) ++count;
}
int find(int p) {
while (p != parent[p]) {
parent[p] = find(parent[p]);
p = parent[p];
}
return p;
}
void unions(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
parent[rootQ] = rootP;
--count;
}
};
class Solution {
public:
int numIslands(vector<vector<char>>& grid) {
int n = grid.size();
if (n <= 0) return 0;
int m = grid[0].size();
if (m <= 0) return 0;
DisjointSet handler;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == '1') handler.insert(i*m+j);
else handler.insert(-1);
//cout << handler.count << endl;
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == '1') {
grid[i][j] = '0';
if (i + 1 < n && grid[i+1][j] == '1') handler.unions((i+1)*m + j, i*m+j);
if (j + 1 < m && grid[i][j+1] == '1') handler.unions(i*m + j + 1, i*m+j);
}
}
}
return handler.count;
}
};
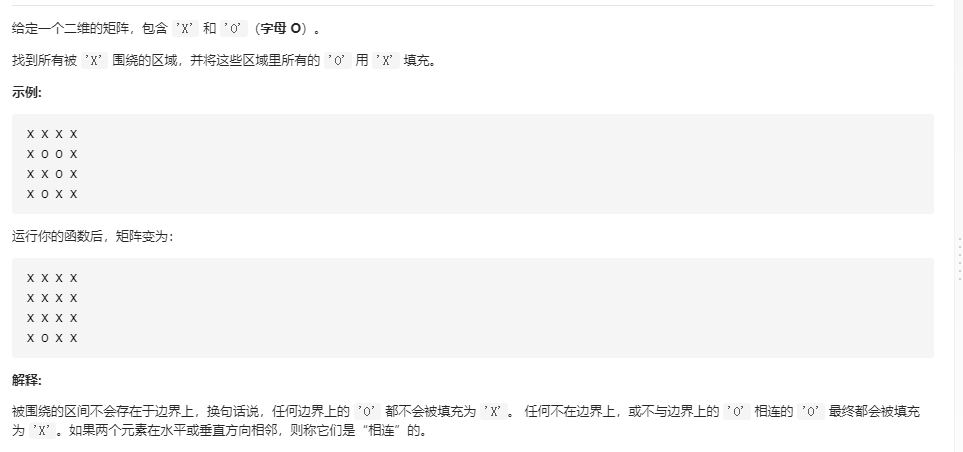
LC.130.被圍繞的區域
-
題意:
![]()
-
思路:并查集方案
- 引用上面的模板,然后增添一個dumy冗余節點,所有邊節點都與之unions,然后所有節點都與其四連通的節點相連,然后最后再遍歷一次判斷與dumy冗余節點相連與否來確定節點是O還是X
class Solution {
public:
void solve(vector<vector<char>>& board) {
int n = board.size();
if (n <= 0) return;
int m = board[0].size();
if (m <= 0) return;
DisjointSet handler(n*m+1);
int dumyNode = n*m;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
// 邊界元素與dumyNode連接
if (board[i][j] == 'O' && (i == 0 || i == n-1 || j == 0 || j == m-1)) {
handler.unions(i*m+j, dumyNode);
}
// 然后下右判斷連接在一起
if (board[i][j] == 'O') {
if (i+1 < n && board[i+1][j] == 'O') {
handler.unions((i+1)*m+j, i*m+j);
}
if (j+1 < m && board[i][j+1] == 'O') {
handler.unions(i*m+j, i*m+j+1);
}
}
} // end for j
} // end for i
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (board[i][j] == 'O' && handler.find(i*m+j) != handler.find(dumyNode)) {
board[i][j] = 'X';
}
}
}
}
};
LC.685.冗余連接II(困難)
-
題意:
- 有向圖
- 有從1——>N的N個節點
- 給出N條有向邊
- 有根樹一般N個節點只需要N-1條邊,但給出N條,因此肯定存在“沖突”或者“循環”或者“循環”+“沖突”
- 任務是找出出現在(給出的有向邊的)最后面的刪去可以使樹合理的邊
-
思路:
- 經分析,只有三大情況:
- 1.純沖突,如1->2,1->3,3->2。此時2有兩個父節點,此時刪去3->2(刪除第二次出現引起沖突的邊)
- 2.純循環,如1->2,2->3,3->1。此時形成循環,刪去3->1(刪去屬于循環的最后出現的邊)
- 3.循環+沖突,如1->2,2->3,3->1,4->1,此時形成循環+沖突,刪去3->1(刪去沖突+循環節點在循環中作為dst的那一條邊)
-
實現:
- 對于純沖突,可以直接開數組(哈希表,因為是從1——>N,所以直接數組就好了)來存儲其父節點編號——>初始化為自身編號,當遇到非自身編號時已證明出現沖突,記錄該有向邊即可
- 對于純循環,使用并查集解決(首先忽略邊的有向性,將能“圍成環”的節點組成一個“集合”)
- 因為只有N條邊,引起沖突時有兩種情況,同時循環或者不循環
- 不循環那直接記錄即可
- 循環,經過上面的思路分析,最后刪除的也是循環內的沖突邊,所以直接記錄該條沖突循環邊即可
- 因為只有N條邊,引起沖突時有兩種情況,同時循環或者不循環
- 這樣通過互斥就解決了有向邊與并查集的矛盾
class Solution {
public:
class UnionSet {
public:
UnionSet(int n) {
parent.resize(n+1);
N = n + 1;
for (int i = 0; i < n+1; ++i) {
parent[i] = i;
}
}
int find(int idx) {
return parent[idx] == idx ? idx: find(parent[idx]);
}
void unions(int i, int j) {
parent[find(i)] = find(j);
}
private:
vector<int> parent;
int N;
};
vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {
int N = edges.size();
vector<int> parent(N+1);
int idx = 0;
for_each(parent.begin(), parent.end(), [&](int& val){val = idx++;});
UnionSet us(N);
int conflictIdx = -1;
int cycleIdx = -1;
for (int i = 0; i < N; ++i) {
if (edges[i][1] != parent[edges[i][1]]) { // 沖突
conflictIdx = i;
} else {
parent[edges[i][1]] = edges[i][0];
if (us.find(edges[i][0]) == us.find(edges[i][1])) { // 循環
cycleIdx = i;
} else {
us.unions(edges[i][0], edges[i][1]);
}
}
}
if (conflictIdx == -1) {
return edges[cycleIdx];
} else {
if (cycleIdx == -1) {
// 先出現的是非循環沖突邊,所以當記錄沖突的時候將循環邊計入循環idx,此時直接返回沖突邊即可
return edges[conflictIdx];
} else {
// 先出現的是循環沖突邊(此時正常計入parent中形成該邊的父子映射),所以當記錄沖突的時候將非循環邊計入沖突idx,通過沖突idx找到沖突循環節點,然后通過parent數組映射到其在循環內的父節點中即可
return {parent[edges[conflictIdx][1]], edges[conflictIdx][1]};
}
}
vector<int> res(2);
return res;
}
};
LC.684.冗余連接
- 題意:與上一題類似,轉換為無向圖
- 因為是無向圖,所以就沒有沖突的說法,即只需要考慮循環,那么刪掉最后一條出現的邊即可(利用并查集直接告訴完成)
class UnionSet {
public:
UnionSet(int len) {
N = len;
parent = vector<int>(N);
for (int i = 0; i < N; i++) parent[i] = i;
}
int find(int p) {
while (p != parent[p]) {
parent[p] = find(parent[p]);
p = parent[p];
}
return p;
}
void unions(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP != rootQ) parent[rootP] = rootQ;
}
private:
vector<int> parent;
int N;
};
class Solution {
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int idx;
int len = edges.size();
UnionSet us(len + 1);
for (int i = 0; i < len; ++i) {
if (us.find(edges[i][0]) == us.find(edges[i][1])) {
return edges[i];
} else{
us.unions(edges[i][0], edges[i][1]);
}
}
return vector<int>(2);
}
};
posted on 2020-08-07 01:01 sacredMoonRainTown 閱讀(72) 評論(0) 收藏 舉報


 浙公網安備 33010602011771號
浙公網安備 33010602011771號