Update on 7.18 好像初步完工了！！！

寫的很簡單，后面在完善。

D1 dp (lyc)

凸性:ppt

邊際效應：對應著決策單調性，兩個東西，同時加上一個東西，多的東西加的多。

二維的邊際效應：四邊形不等式，就是兩條一長一短的線段，同時加一個東西，給長區間加一個東西，比給短區間加一個東西代價更大。

四邊形不等式能推出決策單調性和完全單調性

2D/1D: 形如 \(f_{k,i} + \omega(j,i) \to f_{k+1,j}\),假設 \(\omega(j,i)\) 滿足決策單調性。我們有一個分治做法，能做到 \(O(n k \log n)\)，對于一個區間 \(\left[l,r\right]\)，我們找到中點 \(mid\)，暴力計算，接著直接分治，只不過有決策單調性，可以不用遍歷完。

課上講的是 CF1603D。

完全單調性：對于任意 $ ??<?? $，在一個前綴中從 \(??\) 轉移更好，在一個后綴中從 \(??\) 轉移更好。

二分隊列：

狀態設計技巧:在最優化問題中，一個常用的方法是：
先設計一個取值為 0/1 的狀態，然后利用單調性去掉一維。

舉例子：CF1870E

如果某個轉移區間能被其他東西替代，那么不優。

也可做上面那道題。

還有一個 CF1768F。

WQS二分：

dp 設計原理：感覺是狀態設計。

課上的例題好像忘了（ 這個

但是實際上是這樣的：我們寫考慮判定，再將判定的變量加入 dp。

例題：UOJ748，有點抽象啊

dp of dp:判定換為 dp，一般狀態不會多。

一些奇怪的狀態：Gym103466I（狀壓的東西不太正常）
ABC225F（鄰項交換法，倒序），CF1810G(和前面差不多，wzy 講的)

這里是題解

CF1603D

每一步都很自然的 *3000。

根據上課講的東西，決策單調性顯然，注意到 \(\log_2(k) \geq n\) 時直接能構造出為 \(n\) 的解，然后套用分治即可。還需要一些數論技巧。

CF833B P5574 CF868F

根據上課講的東西，決策單調性顯然。算是三倍經驗了。

P1912

二分隊列。

AT_abc225_f

Sol

CF1810G

在dp選講寫了。

P8321

在dp選講寫了。

CF1870E

有意思題目，第一種做法就是設 \(dp_{i,j}\) 表示 第 \(i\) 項的答案是否能為 \(j\)，讓他成為 0/1 dp。把單調的一維設為狀態。所以是 \(dp_{j} = i\)。類似于 dijkstra 轉移即可。第二種是轉移優化，直接因為本題中，只有極短 mex 區間是有用的。即，若 \(\left[??,??]=[???1,?? \right]\)，或 \(\left[??,??\right]=\left[??,???1 \right]\)，那么這個區間就是無用的。這樣的區間只有 \(??(??)\) 個。

證明看看第一篇題解，多頭上課沒證明出來。（

UOJ748

考慮如何判定這個東西，我們如果能匹配就匹配了，如果不能匹配，我們就直接，讓前面的數當做插入的，保證合法就行。

能我們只需要設 \(dp_{v,x,y}\) 表示已經匹配了長度為 \(v\) 的前綴，插入了 \(x\) 個 0，\(y\) 個 1。轉移不難。

2019 ICPC Nanjing 區域賽 I（QOJ7063）

先考慮 \(1\le a_{i} \le 50\) 怎么做，我們有一個直觀的想法就是對達到的點進行狀壓。顯然不對。但是我們真的需要這樣做嗎，我們只需要把到達的點的權值進行狀壓就行了。直接把這個東西的哈希值放在狀態里面就行了。對于權值 \(\geq 50\) 的情況，我們是不是直接乘上一個組合數進行了。對于 \(0\) 的情況也是同理。

P10141

有一個 \(O(n^4)\) 的 Dp，設 \(dp_{l,r,x}\) 代表在 \(\left[l,r\right]\) 的這個區間，\(x\) 能留下來的概率，這個不好，我們反著做，設 \(dp_{l,r}\) 代表為 \(\left[ l,r\right]\) 這個區間能留下來的概率，是 \(O(n^3)\) 的，這個題后面的部分沒有意義就不寫了。

P2224

P3188

CF1768F

GYM102538H

D2 math (lsy)

?

前面是為后面符號做鋪墊。直接賀 PPT 吧。

上午講的直接賀 PPT 了。疑似太形式化了。

前面是一些 Tricky 東西

后面是容斥原理，二項式反演，子集反演。

賀了一個圖

DAG容斥：？，容斥系數的推導。

GF：講的東西有點 Trivial。

這里是題解

P4159

分層圖，然后做完了。

P10143

考慮算貢獻，分兩種情況， 太簡單了，沒啥好說的。

P7961

經典永流傳屬實了，直接設 \(dp_{i,j,k,l}\) 表示 目前從低到高確定了第 \(i\) 位，目前確定了 \(j\) 個數，目前 \(1\) 的個數為 \(k\)，上一位進位了 \(l\)的所有答案，考慮怎樣轉移，就是轉移到 \(dp_{i+1,j+t,k+(l+t) \bmod 2,l+ \left\lfloor \frac{(l+t)}{2} \right\rfloor }\)，現在來確定一下系數，注意到貢獻是乘積的形式，所以可以乘上 \({n-j \choose t} v_{i} ^ t\)，然后就做完，注意下最后算答案的時候處理一下進位合不合法。

P5664

怎么還是經典題，先考慮容斥，不看最后一條限制，答案是 \(\sum\limits_{i=1}^{n}(1+\prod\limits_{j=1}^{m} a_{i,j}) -1\)，有一個經典的觀察是最多只有一種主要食材不合法，直接枚舉它，我們設 \(dp_{i,j,k}\) 表示前 \(i\)項，不合法的選了 \(j\) 個，合法的選了 \(k\) 個。是 \(O(nm^3)\) 的。注意到當且僅當 \(j-k \geq 0\) 時才能算貢獻，直接把后面那一坨換成差值就可以了，是 \(O(nm^2)\)，可以通過。

AT_arc154_e

不是題目難度差距巨大啊。

怎么感覺這個題不難

需要一點注意力。

前面 \(i^2\) 項對原來的貢獻就是 \({n+1 \choose 2}^m\)，乘起來。

后面不好算，考慮期望乘上總方案數， 就是\(E\left[\sum\limits_{i} i{p_i}\right] = \sum\limits_{i} p_i \times E\left[pos_{p_{i}}\right]\)

上面那一步有點牛，因為他是排列。

首先沒又換過的概率就是 \((1-\frac{(n-i+1)i}{\frac{n(n+1)}{2}})^m\)，期望位置為 \(i\)。

我們考慮一個點 \(i\)。通過一次操作把它挪到點 \(j\) 的方案數顯然是 \(\min(i,n?i+1,j,n?j+1)\)

注意到 \(j\) 和 \(n-j+1\) 本質相同，所以我們期望是 \(\frac{n+1}{2}\)，是不是很牛。概率從前面的減就可以了。

那我們就做完了。

AT_yahoo_procon2019_qual_e

權值和是奇數就是異或和為 \(1\) ，考慮線性基。

我們假設選出了一些行，異或后的序列為 \(B_1,B_2,\dotsb B_m\)。

我們想知道有多少個子集異或為 \(1\)，注意到 \(\forall B_i\)，\(B_i \in \left[0,1\right]\)。我們構造出來線性基，顯然是 \(1\)，對于剩下的 \(m-1\) 個數，對于 \(2^{m-1}\) 可能的情況，都能構造出來他們為 \(1\)，所以就是 \(2^{m-1}\)，但是對嗎？如果我們序列所有數都為 \(0\)，那不就炸了嗎。考慮容斥，我們把每一列的數湊起來看成一個整體，問題變為了一個序列 \(C_1,C_2,\dotsb C_n\)。我們要選出來有多少個子集異或為 \(0\)。那不就是線性基嗎，把所有數加進線性基，答案就是 \(2^{n-線性基大小}\)。還是一樣的道理，線性基內可以構造，外面任選。那們一共就有 \(2^n-2^{n-線性基大小}\) 種合法的，再乘上 \(2^{m-1}\) 可能的情況就行了。

總結：線性基是極大線性無關組的性質一般都是題目的突破口。

感覺挺深刻的。

P3265

不就是線性基板子嗎，注意到線性基是滿足擬陣的。

P4570

從大到小排序，線性基板子。

P3292

我不會告訴你我是樹剖+線段樹過的

現在看來直接倍增就可以了，對的對的。

AT_abc223_h

不難。

P4151

有趣，老題新做。

我們注意到如果只有一條路徑，那們答案直接就是 \(dis_{n}\)，不妨考慮的時候借助生成樹，分析每條非樹邊怎么加進去。我們注意到有一個環的情況，就是異或的時候加上環上一圈的異或值，那么所有的情況是同理的。我們把所有環找出來做一遍線性基即可。還有一個問題，我們到 \(n\) 的路徑不止一條，但是我們是高貴的線性基，所以就是對的！！！

還是一句話：線性基是極大線性無關組。

版本T0相關

實際不全是。

AT_tokiomarine2020_e

P3349

上面兩個都是子集反演。感覺不難。

[CEOI 2019] Amusement Park

經典題*1

我們發現對于一個合法的 DAG，若可以通過原圖操作 \(x\) 次得到，我們也可已通過 \(m-x\) 得到一個反向的合法 DAG，那們變成了一個計數 DAG 個數問題，再乘個 \(\frac{m}{2}\) 就是答案。

第一次做大概率做不出來的，這里直接說怎么做。注意到數據范圍很小，考慮一下狀壓，設 \(dp_{S}\) 點集為 \(S\) 時的答案，對于這一類問題，我們有一種通用的想法，我每一次考慮將一個互相獨立的點的集合加入轉移，如下圖所示：

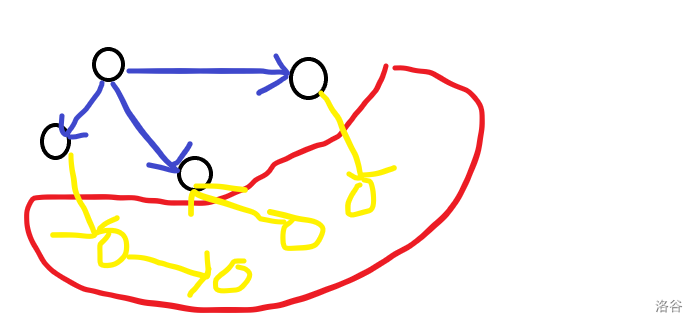
我們直接這樣轉移即可。

但是有問題啊，會算重！！！

還是上圖的例子

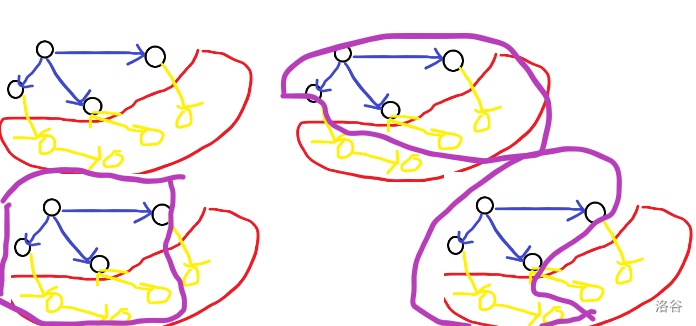
不難發現一個被算了很多次，我們直接容斥，如果互相獨立的點的集合為奇數令他的貢獻為正，否則為負。

寫出來長這樣：

找一個互相獨立的點的集合可以這樣：

rep(i,1,m){
    int a,b;
    cin>>a>>b;
    G[a]|=(1<<(b-1));G[b]|=(1<<(a-1));
}
ok[0]=1;
rep(s,0,(1<<n)-1){
    rep(i,1,n){
        if(s&(1<<(i-1))&&!(G[i]&(s-(1<<(i-1)))))    ok[s]=ok[s-(1<<(i-1))];
    }
}

子集你肯定知道是 \(O(3^n)\) 的。

賀一個題解的話就是：欽定零度點集，簡單容斥去重。

ABC306Ex

經典題*2

考慮沒有等號怎們做，不就是上一個題嗎？

那我們只需要考慮有等號的情況就行了，這個不就等價于縮點嗎，預處理所有可能的情況，用并查集維護一下聯通塊大小，和上一個題沒有區別。

拉插優化dp

難點在于想到拉插，可以看看這一篇是如何找到次數的。

省流：差分！！！

lsy給的題不多，經典題還是自己找一找。

Day 3 樹上ds,圖論相關 （lsy）

最開始有點 Trivial。

前面東西總結一下：

1. 盡量使用基本的技巧，轉化為經典問題
2. 根據信息結構的強弱，使用不同的東西維護。
3. 倍增維護等冪信息，這個只需要不漏，樹上差分要想的起來。

重剖：candy。

長鏈剖分：我好像寫過一點，但是還有優化 dp。

線段樹合并：今天主要不是基礎，是線段樹合并優化 dp。
其他的總結是線段樹合并+樹上差分可以做到“在恰當的時刻擁有想要的信息”

還是寫一下優化 dp 吧。

要滿足一些條件，有用的值是 \(sz\) 個，并且后面那一坨是一堆相乘的形式。實際上是整體 dp。

dsu on tree:本身簡單，今天講的題有點抽象，一個 Trick 是枚舉 LCA。

最小生成樹：我們不一定要用，主要是 3 種求法的思想各有各的用處。

生成樹相關構造與 dfs 樹：dfs 樹具有不存在橫叉邊的性質。

點雙：圓方樹，不解釋/wx。

強連通性：今天學會了 kosaraju ！！！，對于正圖dfs，記錄出棧時間戳，在反圖從大到小 dfs。

耳分解

雙極定向

2-SAT：今天的技巧是將 \(X_{i,j}=[a_i\le j]\) 作為條件。

歐拉回路：dfs，回溯時加入當前點。

這里是題解。

CF888G

考慮 Boruvka，注意：這一種題目中，我們往往只是借鑒了它的思想。

我們逐位進行考慮，對于在 \(w\) 這一位中，我們將 \(0\) 與 \(1\) 的分開考慮。

我們在一側的 root 上面直接套用經典做法找到異或最小值，然后將 \(0,1\) 兩側的樹合并即可，注意到這樣的話權值還要加上 \(2^w\)。

CF1364D

把 dfs 樹建出來，至于相關的東西，在圖論雜題寫過。

無向圖 dfs 樹是沒有橫插邊的。

如果能找到合法環就找，不能直接找獨立集。正確性顯然。

Public Judge Round 3, A

考慮 Boruvka，我們對于中間的點，只能向上或向左連一條邊，然后將最外面的邊直接連起來。

UOJ176

Boruvka。

P8820

111

P4577

課上講的是dsu on tree (記得哪天寫一下這個)

我們考慮 dp，設 \(dp_{i,j}\) 表示 以 \(i\) 為根的這一棵子樹，此時的選的最小值為 \(j\)，

有以下轉移

第一個正常的對每一個節點開一顆線段樹，直接往上轉移。

第二個考慮線段樹合并優化，因為沒怎么寫過所以寫的比較詳細。

對于兩顆線段樹 x 和 y，我們進行分類討論。

可以畫圖更有助于理解

維護 \(x\) 右邊的 \(\sum\limits{dp_{v,\geq j}}\)，叫做 \(maxp\) ，另外一側叫做 \(maxq\)

1.\(x=0,y=0\) 直接返回。

2.\(x=0,y \neq 0\) 直接給 y 上的節點區間加 maxp。

3.\(x \neq 0,y = 0\) 直接給 x 上的節點區間加 maxq。

4.\(x \neq 0,y \neq 0\) 線段樹合并上去。

int y1=t[rs(y)].val,y0=t[rs(x)].val;
ls(x)=merge(ls(x),ls(y),l,mid,max(maxp,y0),max(maxq,y1));
rs(x)=merge(rs(x),rs(y),mid+1,r,maxp,maxq);

對于左子樹，我們要加上右子樹的那一坨東西。

這個題對對于右子樹，不需要管。

最后 dp 過程大概是這樣的

void dfs(int u,int fa){
    int val=1;
    for(int i=h[u];i;i=g[i].nxt){
        int v=g[i].v;
        if(v==fa)   continue;
        dfs(v,u);
        val+=query(root[v],a[u],Lim,0,Lim);
        root[u]=merge(root[u],root[v],0,Lim,0,0);
    }
    modify(root[u],0,Lim,a[u],val);
}

P5298

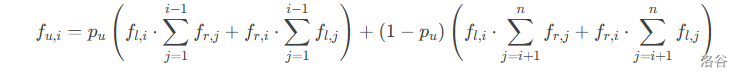
轉移是這個，我們只需要維護前綴和，后綴和，我們考慮線段樹合并優化 dp。

1.\(x=0,y=0\) 直接返回。

2.\(x=0,y \neq 0\) 直接給 y 上的節點區間乘 maxp。

3.\(x \neq 0,y = 0\) 直接給 x 上的節點區間乘 maxq。

4.\(x \neq 0,y \neq 0\) 線段樹合并上去。

int merge(int x,int y,int sumx,int sumy,int pbmax,int pbmin){
    if(!x){mktag(y,sumx);return y;}
    if(!y){mktag(x,sumy);return x;} 
    pushdown(x),pushdown(y);
    int x0=t[ls(x)].val,x1=t[rs(x)].val,y0=t[ls(y)].val,y1=t[rs(y)].val;
    ls(x)=merge(ls(x),ls(y),(sumx+pbmin*x1)%mod,(sumy+pbmin*y1)%mod,pbmax,pbmin);
    rs(x)=merge(rs(x),rs(y),(sumx+pbmax*x0)%mod,(sumy+pbmax*y0)%mod,pbmax,pbmin);
    pushup(x);return x;
}

CF1697F

難點在于想到2-SAT。

Trick:將 \(X_{i,j}=[a_i\le j]\) 作為條件。

CF1583H

你管這個叫 *3300？

第一問從大到小加入，用并查集維護。

第二問就則略微不同，我們考慮如何合并兩個集合，如果最大值不相等直接并查集完事，如果相等，我們可以在兩邊的集合中取 max，但是還有中間的東西，但我們只需要求最大費用就可以，所以隨便找一條路徑，取一個最大值就行了。這種做法相當于建了隱式的重構樹。

長鏈剖分的題

看到我記得讓我催更

連通性相關題目

看到我記得讓我催更

Day 4 ds lyc

是不是最開始沒講的部分才是最有趣的

最開始就是經典的矩陣規約。多頭是不是講的有點水

四毛子: 實際上是 log 分塊。

這里只有 +1-1RMQ。

我們取一個閾值 \(B\)，一共有 \(\dfrac{n}{B}\) 個塊，然后對于整塊直接維護 \(\dfrac{n}{B}\) 個ST表，這個是 $ O(\dfrac{n}{B} \log \dfrac{n}{B})$ 的。

實際上，我們研究一下本質，實際上我們要解決的問題是，如果兩個點在一個塊里面，我們如何求出最值，因為不在一個 塊時，維護前后綴就可以了，我們需要充分利用好性質，對于長度小于等于 \(B\) 的長度，我們注意到一共只有 \(2^{B}\) 種可能，總的復雜度是 \(O(B 2^B)\) 的。令 \(B= \frac{\log n}{2}\) ，此時是線性的。

講 \(??\) 叉樹 是不是還是有點魔怔了，我是不是直接可以取 \(e\) 的到理論最優復雜度。

接下來并不是 PPT 上的內容。

我們考慮維護 ds 我們要干什么。

1.信息的性質，例如結合律，以及前幾天 feecle 講課提到的那些。

2.靠近經典問題。

3.在線，離線，注意：這個和我們平常說的強制在線之類的是有區別的。，真正的在線的東西只有二分，但是好像不止吧，好吧實際上還有自動機的構造，例如莫隊指針的偏移，我們需要查詢一些信息，用來統計答案，這些東西顯然不是強制在線的，所以我們在離線把這些信息處理，這就是所謂的“二次離線”。

4.勢能，看下面。撤銷：e.g. 可撤銷并查集，線段樹分治，回滾莫隊。

根號分治：今天講的題目難點不在于這個，之前有過總結就不寫了。

勢能分析：這應該是比較正（che）統 （dan）的。

經典問題：區間開根，區間和。

sol:我們的勢能是區間 max。每一次向下開根，都會變小很多。

同樣是經典問題：區間開根，區間和，區間加。

sol: 令勢能 \(\sum \log(\log |a_i-a_{i-1}| +1)\)

不要看上去很嚇人，實際上很多都是類似形式。

1.若勢能為 0，即區間所有數相同，實際上還要特判極差為1的情況，無須遞歸下去開根；

2.若遞歸下去開根了，區間的勢能至少 ?1；

3.每次區間加，勢能增加是 \(??(\log \log n)\) 的。

所以只需維護區間是否相同。

減半報警器：。

這里是題解

莫隊二離

模板題

首先暴力莫隊過不去。

我們考慮將 $\left[L,R\right] \to $ 其他地方的貢獻算上。

將\(\left[L,R\right]\) 對 \(x\) 的貢獻記作 \(g\left(L,R,x\right)\)

1. $ \left[L,R \right] \to \left[L,R+k\right] $

就是求對于在 \(\left [R+1,R+k \right]\) 的 \(x\)，求出 \(g(L,x-1,x)\)

差分之后就是 $g(1,x-1,x) - g(1,L-1,x) $，前面的東西，我們可以直接算出來，而后面的東西，我們再次離線，就像這樣給他打上一個標記

g[L-1].push_back({R+1,q[i].r,-i});

同理我們可以寫出整個過程。

P3350

dp選講寫過了。

P8564

樹上背包，我們可以采用上下界優化，做到 \(O(n^2)\) 的復雜度。

區間推max/min

維護最大值，次大值，最大值次數。

Day 5 flow,分治 （lsy）

原來的 blog 寫了一點基礎問題。

上午的題目非常的有意思。

CF1250K 這個題告訴我們一些事情，我們可對于網絡流問題，我們第一個點是找到一個非常容易的數學模型，第二個是對于一個結論，可以猜測必要性推測充分性。

CF1684G 這個題也是找到一個非常容易的數學模型，如果找到了這個題建二分圖是非常自然的事情。

P4003:費用流入門題目，注意力驚人。

Primal Dual 算法：實際上是勢能 dijkstra，可以看看以前寫的。

費用流問題，每一單位流量的最短路長度單調不減。

最小割的實質：假設 \(x_i\) 表示 \(i\) 是不是和 \(S\) 在一邊，則目標就是最小化

注意:問題只能轉化成這種形式，否則是 NP-hard的

題目非常有意思，后面放上來。

模擬網絡流，費用流

P5470：模擬費用流入門題。
建圖之后要大力分類，感覺挺抽象的。

下午的題目還是很有有趣的，感覺 PPT 寫的很詳細，等我做了在放上來。

這里是題解。

我好像有些不會做。

CF1684G

好題。

我們考慮怎們構造，因為這個和上課內容無關，所以我們直接寫了。

對于 \(t_i \leq \dfrac{m}{3}\)，直接構造 \((3m,2m)\) 就可以了。

對于 \(t_i > \dfrac{m}{3}\)，最優秀的構造是 \((2p+x,p+x)\)，其中 \(p> \dfrac{m}{3}\)，\(x < \dfrac{m}{3}\)，這個代表對于一個 \(p\)，至少需要一個 \(p\) 去與它匹配，還要只產生這兩個數。判斷一下是否同余。然后建立二分圖跑一個二分圖匹配就行了。

P8215

最小割模板題目。

變量是什么：每個人參與或者不參與，每個團隊愿意或者不愿意。

對于第一個限制。直接 \(S\) 向 \(i\) 連 \(d_i\)，\(i\) 向 \(T\) 連去 \(c_i\)。

真的按上課那個套路感覺沒什么難度，懶得寫了。

P3227，P6054

別急。

P4313

把所有貢獻減去最小割。

真的按上課那個套路感覺沒什么難度，懶得寫了。

AT_arc142_e

前置：二分圖最大權獨立集：求二分圖最大權值和的獨立集。

先設 \(x_i\) 表示 \(i\) 選不選，然后把一邊的變量取反。

偉大，無需多言。

這個是真的困難。

我們實際上的限制是

后面那個拆開之后實際上是

直接調整就可以了。

切糕和一些 2-SAT 的題目告訴我們我們題目的變量可以是形如 \(X_{i,j}=[a_i \leq j]\) 的東西是可以作為變量的。我們嘗試直接做，但是條件是 \((\lnot x_{i} and \lnot x_{j})\) 并不能直接做，所以這個題做不了

觀察一下，如果有一個下界已經 $ \geq \max?(??_x,b_y)$ 就不用考慮了。

如果沒有了，這個限制意味著什么，我么要讓其中一個東西大于$ \geq \max?(??_x,b_y)$，這個東西好像對于一組限制，就已經是二分圖，對于左側的，就是 \(a_i<b_i\)，另外一側是 \(a_i \geq b_i\)，我們直接轉換成為 \((x_{i} and \lnot x_{j})\)，好了這個就是二分圖的形式。

不要急，我們還沒有考慮每一個變量的限制。

有一個顯然的東西是$i+1 \to i $ 連接 INF。

不是剩下的都很顯然啊，不寫了。后面就是上課講的基礎東西。

AT_arc125_e

Link

CF1442D

有意思的。

我們注意到最優的選擇一定是只有一個沒有選完，其他的都選完了。

暴力 dp 是枚舉只有一個沒選完的點 \(x\)，將 \(1,2,3,\dots x-1,x+1,\dots,n\) 加入 dp，這個是 \(O(nk^2)\) 的。

考慮分治，solve(l,r) 這個東西表示已經將 \(\left[1,l-1\right] \cup \left[l+1,n\right]\) 的東西加入了背包，那對于 \(solve(l,mid)\)，我們只需要將 \(\left[mid+1,r\right]\) 加入背包，回溯是回退即可。

solve(l,l) 就是答案。

P7482

沒有意思題。

直接暴力維護 \(4\) 個 dp 數組，分別為左端點可以選或一定不選的的獨立集，右端點可以選或一定不選的的獨立集。然后分治算貢獻就行了。

P4755

最值分治，很有趣的套路，如果貢獻和最值相關，我們直接對最值進行分治，每次只需要枚舉小區間，算它對大區間的貢獻，感覺你可以叫他啟發式分裂。

P5654

以后我一定要學會線性求笛卡爾樹！！！

考慮將詢問拆開，我們以左端點為例，對于 \(\left[l,r\right]\) 這個點，從\(\left[w+1,r\right]\) 來的的貢獻不改，只需改另外一側就行了，只需要ds維護就行了。

P9058

遇見樹上路徑問題，考慮點分治。

那們直接轉化為 \(dis_u+dis_v\) 就是對的，但是這樣的點對太多，很多都沒有用，他們可以被其他東西偏序掉，這個東西就叫做支配對。

在這個題目中，我們只需要找到他們的前后繼就行了，一共只有 \(O(n \log n)\) 個，用單調棧維護，最后是一個類似二維數點的形式，代碼并不難。

P5979

feecle:這個題很簡單，我們就不講了。

P2305

出棧序+李超線段樹套線段樹

CF1373F P6122 P3826 P4214 P3980 CF1427G CF1666K P1792 CF2029I

還沒有看。

Day 6 紙糊串

我會哈希，你會嗎。

內容和這個高度重合，看看這個吧。