題目：基于Simulink的SSB信號調制與解調仿真

參考文章

一、實驗目的與要求

• 目的：學習SSB信號的調制與解調仿真
• 要求：
  1. 具有MATLAB的仿真結果并附上代碼
  2. 具有基于Simulink的模塊的模擬仿真結果，并附上設計模塊圖
  3. 結果清晰充分
  4. 包含實現結果分析和總結

二、原理

1. 單邊帶調制是幅度調制的一種，由調制信號去控制高頻載波的幅度，使之隨調制信號做線性變化的過程。這里的線性并不意味著已調信號與調制信號之間符合線性變換關系，事實上，任何調制過程都是非線性變換過程。
2. SSB信號是將DSB信號中的一個邊帶濾掉而形成的，最直接的方法是濾波法。所謂濾波法，就是通過產生一個雙邊帶信號，然后讓其通過一個邊帶濾波器，即可得到單邊帶信號。
   其中,
     DSB信號為：\(s_{DSB}(t)=m(t)cosw_ct\)

?? DSB信號頻譜為：\(S_{DSB}(t)=\frac{1}{2}[M(w-w_c)+M(w+w_c)\)

?? SSB信號為：\(s_{SSB}(t)=s_{DSB}(t)*h_{SSB}(t)\)

?? SSB信號頻譜為：\(s_{SSB}(t)=\frac{1}{2}[M(w-w_c)+M(w+w_c)H_{SSB}(t)\)

3. 解調采用相干解調，也叫同步檢波。解調與調制的實質一樣，均是頻譜搬移。調制是把基帶信號的頻譜搬移到載頻的位置，這一過程可以通過一個相乘器與載波相乘來實現。解調是調制的反過程，即把在載波位置的已調信號的頻譜搬回到原始基帶位置，因此同樣可以使用相乘器與載波相乘來實現。
   即：????????\(S_p(t)=S_m(t)cosw_ct\) ,

   其中，\(cosw_ct\)為相干載波，\(S_m(t)\)為SSB信號

4. 實際上，各種線性已調信號在傳輸過程中不可避免的要受到噪聲的干擾，所以在解調過程中需要解調器的抗噪聲性能足夠的強，也就是信噪比增益越高，解調器抗噪聲性能越好。
   其中信噪比增益為：\(G=\frac{S_o/N_o}{S_i/N_i}\)

利用濾波法展示單邊帶信號框圖

單邊帶信號頻譜圖（分上邊帶、下邊帶）

相干解調框圖

線性調制相干解調是接收系統的一般模型

其中\(n(t)\)為加性高斯白噪聲\(s_m(t)\)為已調信號，BPF為帶通濾波器，解調器為相干解調器；\(n_i(t)\)為窄帶高斯噪聲，\(m_o(t)\)為輸出的有用信號，\(n_o(t)\)為噪聲

 

三、實驗內容

一、基于Simulink的SSB調制實驗(純正弦)

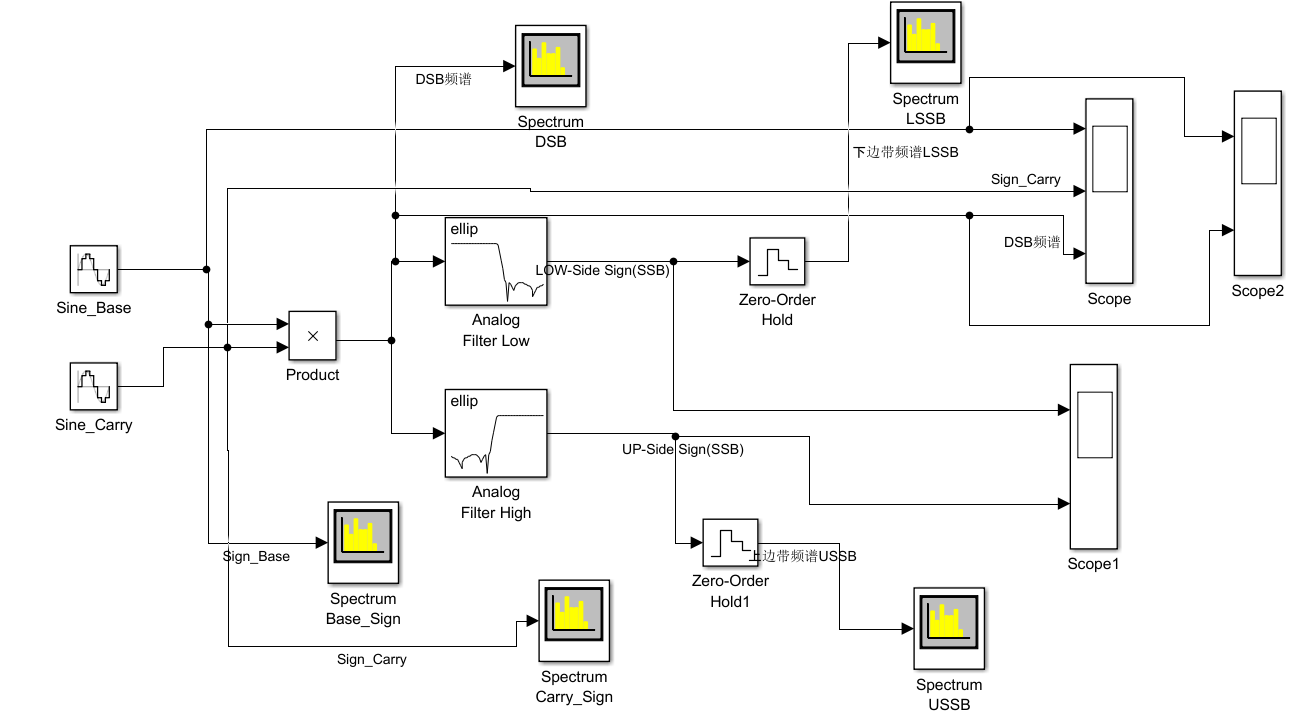
圖注：基于Simulink的SSB調制模塊圖

模塊結構:

• 輸入： 一個2Hz的正弦基帶信號和一個20Hz的正弦載波信號，其中基帶信號為\(2sin(4\pi)\),載波信號為\(2sin(40\pi)\)
• 邊帶濾波器： 采用的是橢圓模擬濾波器，過渡帶比較窄。其中低通濾波器的通帶邊界頻率為20-2=18Hz,高通濾波器的通帶邊界頻率為20+2=22Hz，兩個濾波器的通帶最大衰減均為0.1dB，阻帶最小衰減均為80dB

圖注：第一個波形為：消息信號（2Hz）第二個波形為：載波信號 (20Hz)

第三個波形為：DSB已調信號

• 從上圖可以看到DSB波形，在過零點處有相位翻轉180°的現象，幅值為4

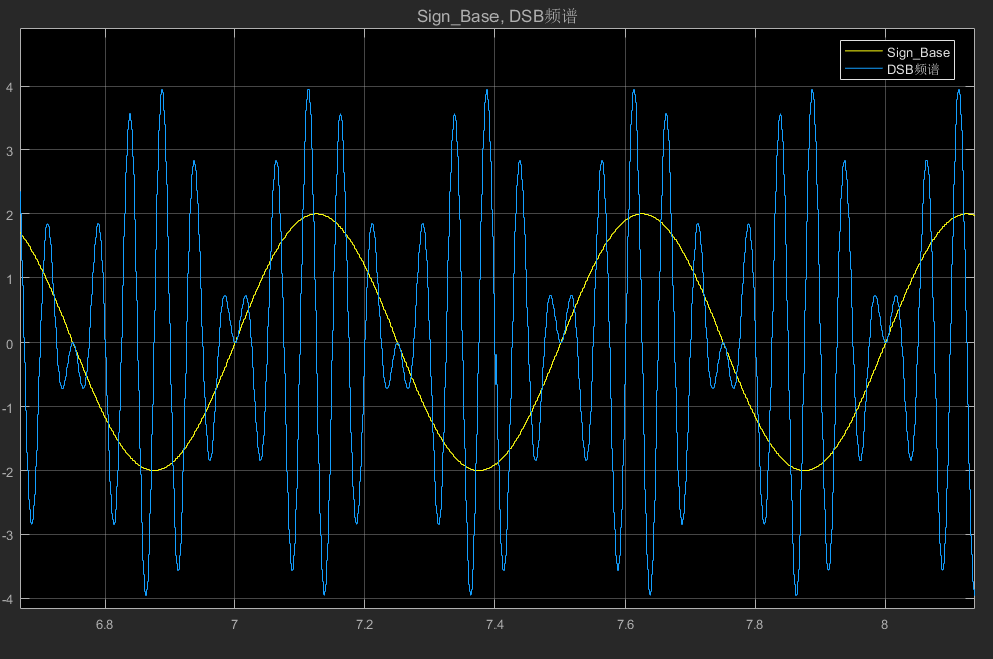
圖注：黃色波形為：基帶信號

藍色波形為：DSB已調信號

• 可以看到基帶信號經過DSB信號過零點處

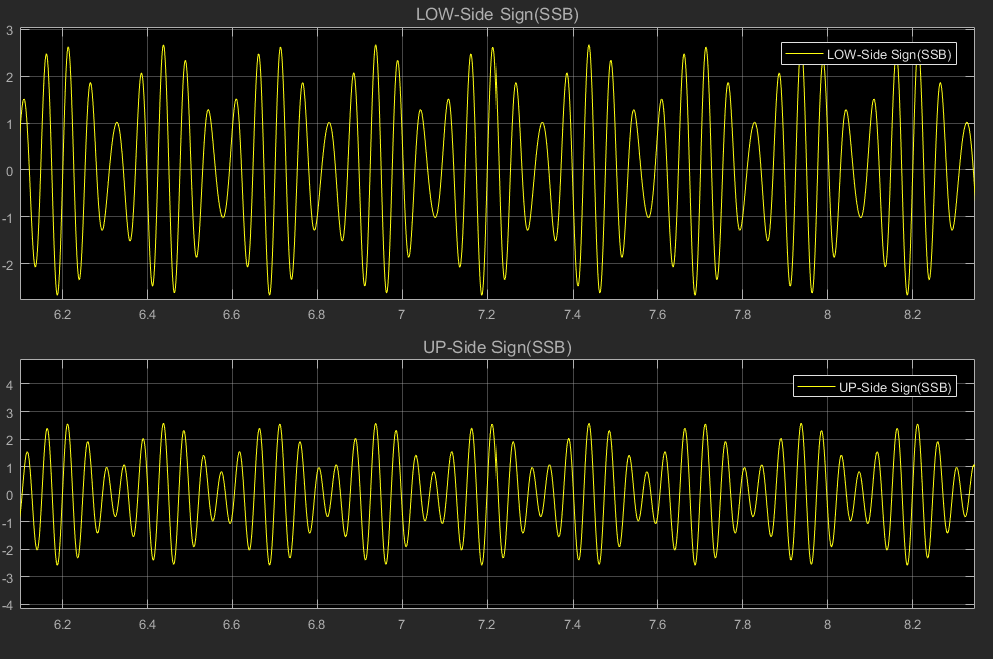
圖注：第一個波形為：下邊帶信號（LSSB）

第二個波形為：上邊帶信號（USSB）

圖注：基帶信號頻譜

• 可以看到一個頻率為2Hz，幅值為2的正弦信號頻譜

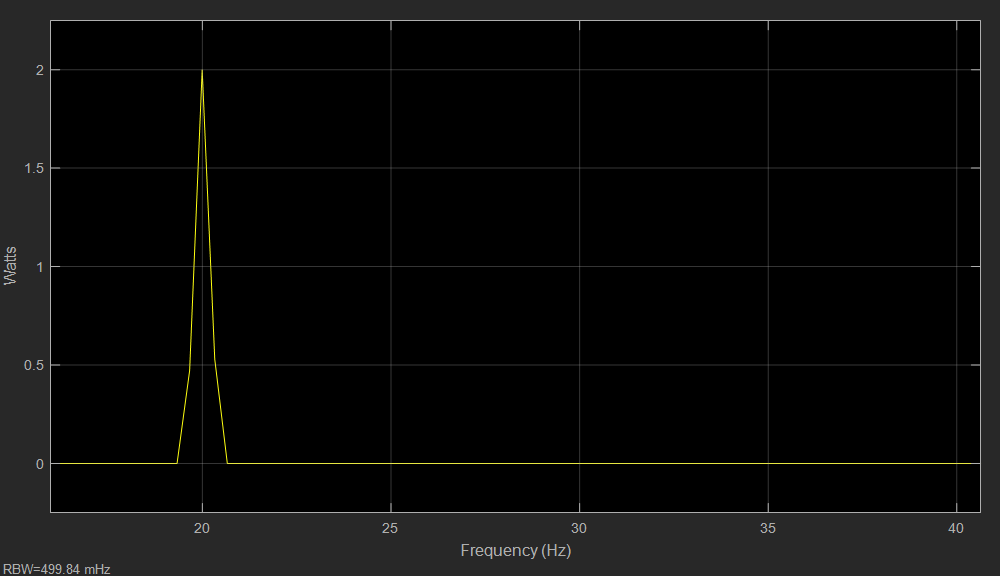
圖注：載波信號頻譜

• 可以看到一個頻率為20Hz，幅值為2的正弦信號頻譜

圖注：DSB信號頻譜

• 可以看到有兩個邊帶，其中下邊帶主要頻率成分為18Hz，幅值為2；上邊帶主要頻率成分為22Hz，幅值為2；

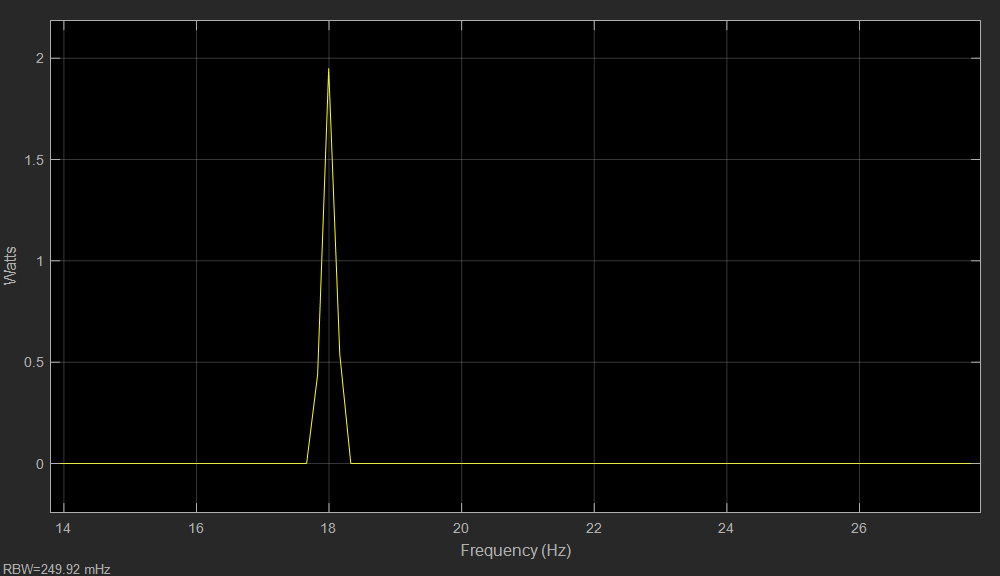
圖注：LSB信號頻譜

• 可以看到上邊帶基本沒有了，主要頻率成分為18Hz，幅值為2的下邊帶信號頻譜

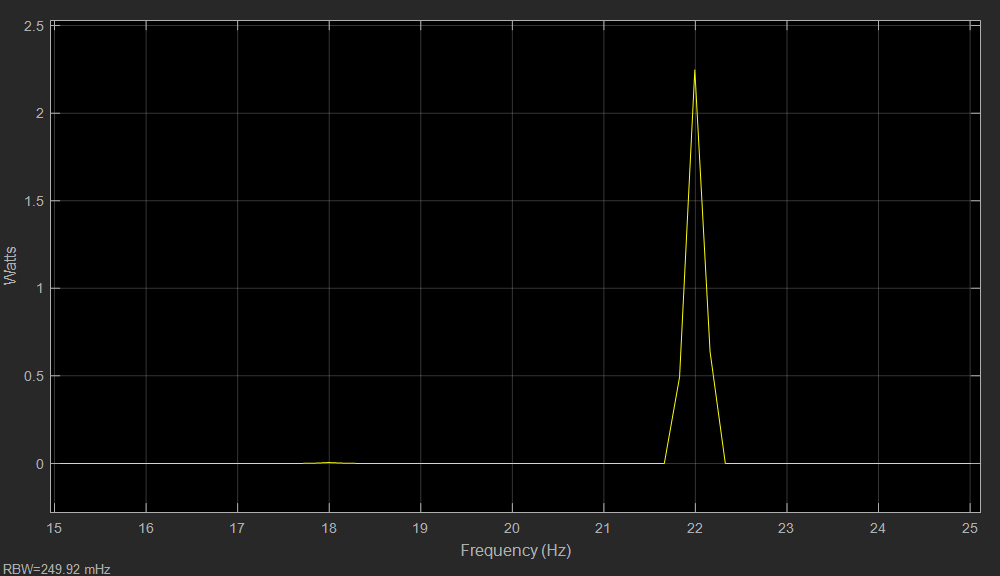
圖注：USB信號頻譜

• 可以看到下邊帶基本沒有了，主要頻率成分為22Hz，幅值為2的上邊帶信號頻譜

小結： 通過把兩個信號直接相乘來產生DSB信號，這種調制會把基帶信號的頻譜搬移到載波信號的頻譜附近，形成對稱的上下邊帶，所以從信息傳輸的角度考慮，僅需要任一邊帶就夠了，所以通過適當的低通濾波器取得下邊帶，適當的高通濾波器取得上邊帶。這里原本的濾波器采用Butterworth濾波器的設計方式，但由于過渡帶不夠窄，即不夠陡峭，總是會殘留一部分邊帶，再經過查閱資料后選擇了過渡帶比較窄的橢圓濾波器，這樣就基本濾除了另一個邊帶。

二、基于Simulink的SSB相干解調實驗(純正弦)

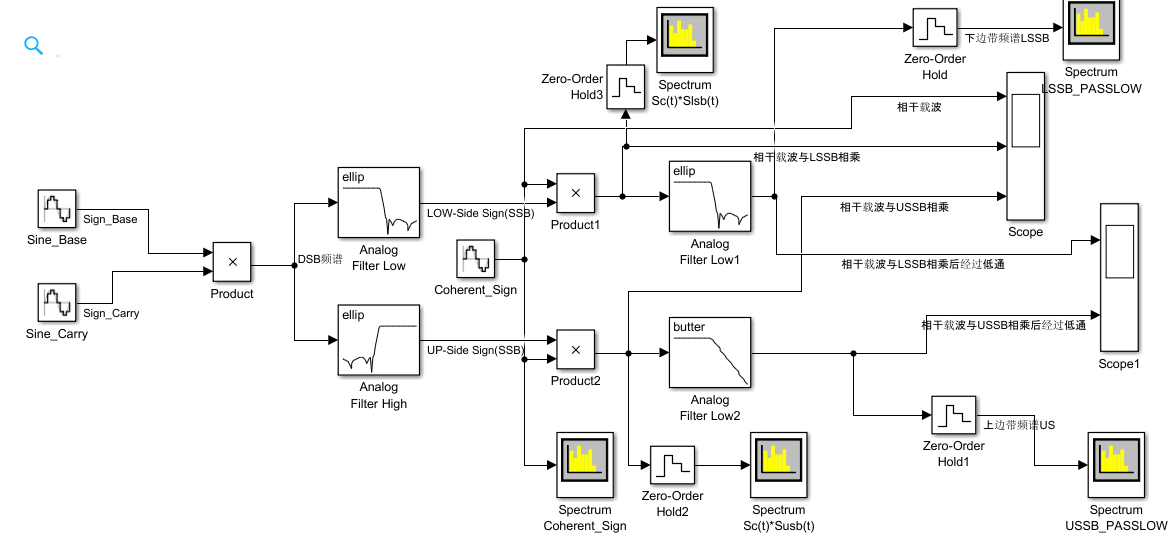
圖注：基于Simulink的SSB解調模塊圖

模塊結構:

• 輸入： 一個2Hz的正弦基帶信號和一個20Hz的正弦載波信號，其中基帶信號為\(2sin(4\pi)\),載波信號為\(2sin(40\pi)\)
• 邊帶濾波器： 采用的是橢圓模擬濾波器，過渡帶比較窄。其中低通濾波器的通帶邊界頻率為20-2=18Hz,高通濾波器的通帶邊界頻率為20+2=22Hz，兩個濾波器的通帶最大衰減均為0.1dB，阻帶最小衰減均為80dB
• 相干載波： \(2sin(40\pi)\)與輸入時的載波信號同頻同相
• 低通濾波器 ： 通帶邊界頻率為40Hz的橢圓模擬低通濾波器

圖注：波形1為：相干載波（20Hz）

波形2為：相干載波與LSB信號相乘后的波形
波形3為：相干載波與USB信號相乘后的波形

• 可以很明顯看到波形2和波形3基本是相同的

圖注：波形1為：相干載波與LSSB信號相乘后經過低通后的波形

波形2為：相干載波與USSB信號相乘后經過低通后的波形

• 可以看到圖中標注的兩個信號再經過LPF后的波形一致，且頻率為2Hz，幅值為2，與基帶信號一致，說明上下邊帶所含的信息一樣，解調成功。

圖注：相干載波與LSB信號相乘后的波形頻譜

• 相干載波與LSB信號相乘后的波形頻譜在20-18=2Hz處有一個信號，在18+20=38Hz處也有一個信號，符合DSB調制的規律

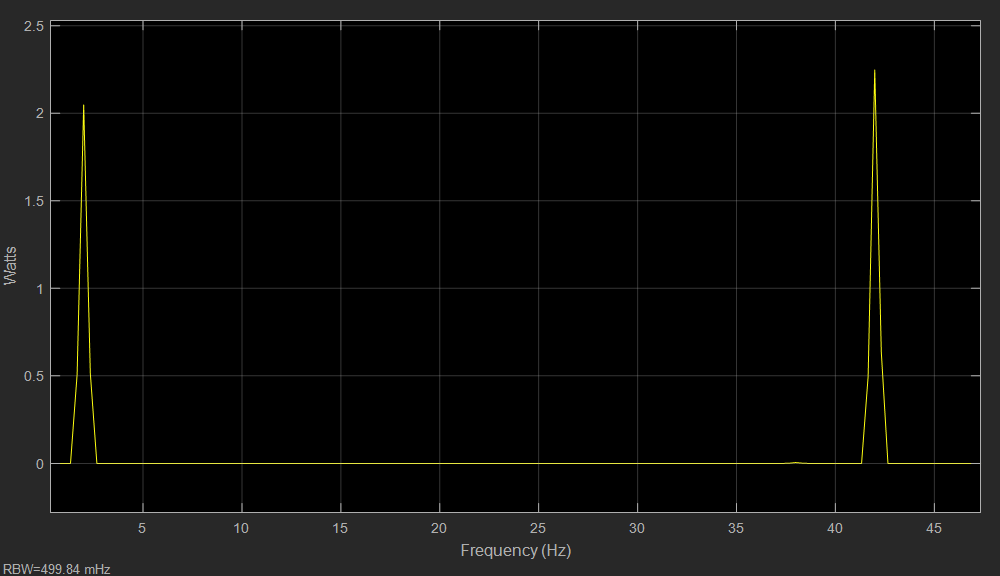
圖注：相干載波與USB信號相乘后的波形頻譜

• 相干載波與USB信號相乘后的波形頻譜在-20-(-22)=2Hz處有一個信號，在20+22=42Hz處也有一個信號，符合DSB調制的規律。對比上面相干載波與LSB信號相乘后的波形發現，在2Hz處都有一個相同幅值的信號。

圖注：相干載波與LSB/USB信號相乘后經過低通后的波形頻譜

• 可以看到相干載波與LSB/USB信號相乘后經過低通后的波形頻譜都是一樣的，為頻率2Hz,幅值為2的正弦信號。

小結： 通過從DSB信號經過單邊帶濾波器取得任一邊帶形成的SSB信號，與相干載波相乘后，形成的信號基本一樣，再通過適當的LPF后就可得到基帶信號。其中，相干載波要與DSB調制時的載波同頻同相，從步驟上來看與DSB調制本質上一樣。最后的結果說明用上邊帶或下邊帶都可以解調出基帶信號。

三、基于Matlab的SSB調制

• 實驗代碼

%DSB design
clear all;
Fs=1024;%采樣頻率
t=0:1/Fs:2;%信號長度
Am=2;%基帶信號幅值
Ac=2;%載波信號幅值
fm=2;%基帶信號頻率
fc=20;%載波信號頻率
wm=2*pi*fm;%基帶信號模擬角頻率
wc=2*pi*fc;%載波信號模擬角頻率
Sm=Am*sin(wm*t);%基帶信號
Sc=Ac*sin(wc*t);%載波信號
SDSB=Sm.*Sc;%DSB已調信號
spec_SDSB=fft(SDSB,2*Fs);%對DSB信號做2048點FFT，做頻譜分析
mag_SDSB=abs(spec_SDSB);%計算DSB頻響幅值
fdsb=(0:2*Fs-1)./2;%真實頻率

figure(10);
plot(fdsb,mag_SDSB);grid on;%顯示DSB頻譜
title('DSB Spectrum');
set(gca,'xlim',[10,30]);

figure(1);
plot(Sm);grid on;%顯示基帶信號
title('Base Sign');
set(gca,'xlim',[0,1000]);
figure(2);
plot(Sc);grid on;%顯示載波信號
title('Carry Sign');
set(gca,'xlim',[0,1000]);
figure(3);
plot(SDSB);grid on;%顯示DSB信號
title('DSB Wave');
set(gca,'xlim',[0,1000]);

%filter design
N=8;%橢圓濾波器的階數
[BL,AL]=ellip(N,0.1,80,(fc-fm)/(Fs/2),'low');%設計橢圓低通濾波器
%其中通帶最大衰減為0.1，阻帶最小衰減為80，通帶邊界頻率為20-2=18Hz
[H1,F1]=freqz(BL,AL,Fs/2,Fs);%獲取濾波器的頻響函數
[BH,AH]=ellip(N,0.1,80,(fc+fm)/(Fs/2),'high');%設計橢圓高通濾波器
%其中通帶最大衰減為0.1，阻帶最小衰減為80，通帶邊界頻率為20+2=22Hz
[H2,F2]=freqz(BH,AH,Fs/2,Fs);%獲取濾波器的頻響函數

figure(4);
plot(F1,20*log10(abs(H1)));grid on;%顯示橢圓低通濾波器的頻響
title('Ellips low pass filter');
set(gca,'xlim',[0,100]);
figure(5);
plot(F2,20*log10(abs(H2)));grid on;%顯示橢圓高通濾波器的頻響
title('Ellips hign pass filter');
set(gca,'xlim',[0,100]);

%SSB design
LSSB=filter(BL,AL,SDSB);%DSB經過Ellips LPF后取得下邊帶
USSB=filter(BH,AH,SDSB);%DSB經過Ellips HPF后取得上邊帶

figure(6);
plot(LSSB);grid on;%顯示下邊帶波形
title('LSSB Wave');
set(gca,'xlim',[0,1000]);
figure(7);
plot(USSB);grid on;%顯示上邊帶波形
title('USSB Wave');
set(gca,'xlim',[0,1000]);

spec_LSSB=fft(LSSB,2*Fs);%對LSSB信號做2048點FFT
spec_USSB=fft(USSB,2*Fs);%對USSB信號做2048點FFT
mag_LSSB=abs(spec_LSSB);%計算LSSB頻響幅值
mag_USSB=abs(spec_USSB);%計算USSB頻響幅值
fssb=(0:2*Fs-1)./2;

figure(8);
plot(fssb,mag_LSSB);grid on;%顯示LSSB頻響幅值
title('LSSB Spectrum');
set(gca,'xlim',[10,30]);
figure(9);
plot(fssb,mag_USSB);grid on;%顯示USSB頻響幅值
title('USSB Spectrum');
set(gca,'xlim',[10,30]);

圖注：基帶信號

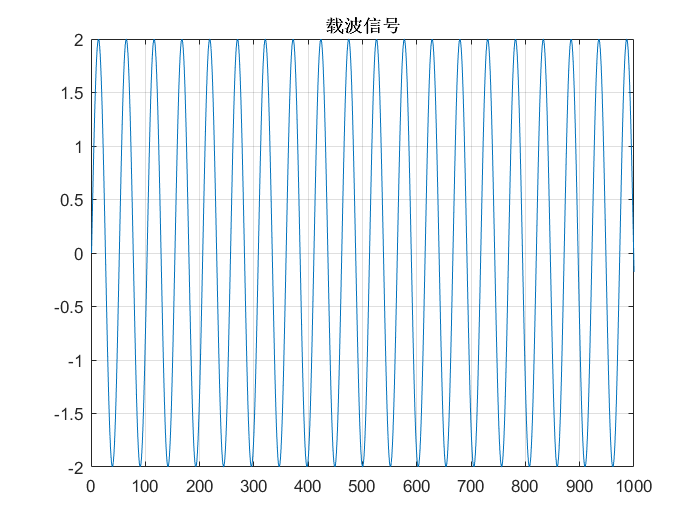
圖注：載波信號

• ·基帶信號： 頻率為2Hz，幅值為2，其時域表達式為\(2sin(4\pi)\)
• ·載波信號： 頻率為20Hz，幅值為2，其時域表達式為\(2sin(40\pi)\)

圖注：DSB已調信號波形

• 從上圖可以看到DSB波形，在過零點處有相位翻轉180°的現象，幅值為4

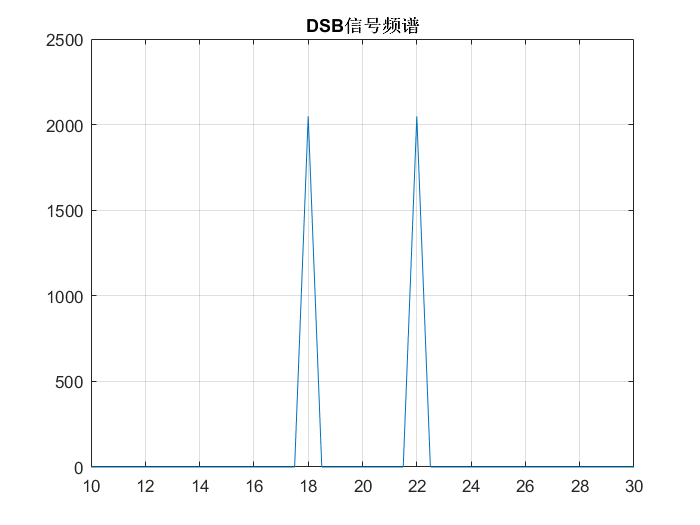
圖注：DSB已調信號頻譜

• 可以看到有兩個邊帶，其中下邊帶頻率為18Hz，幅值為2；上邊帶頻率為22Hz，幅值為2，因為做2048點FFT，所以這里的幅值是2048。

圖注：橢圓低通濾波器頻響

• 可以看到通帶邊界頻率為18Hz，通帶最大衰減基本為0，阻帶衰減最小為80,過渡帶比較窄，有較大的陡峭度，可以很好的濾除上邊帶

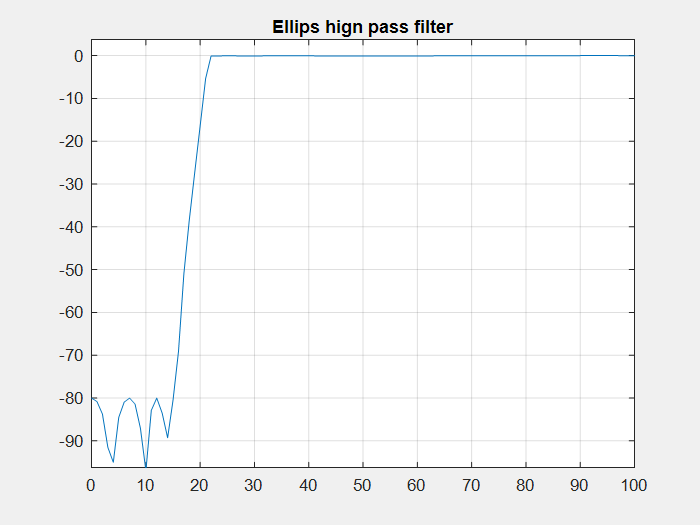
圖注：橢圓高通濾波器頻響

• 可以看到通帶邊界頻率為22Hz，通帶最大衰減基本為0，阻帶衰減最小為80,過渡帶比較窄，有較大的陡峭度，可以很好的濾除下邊帶

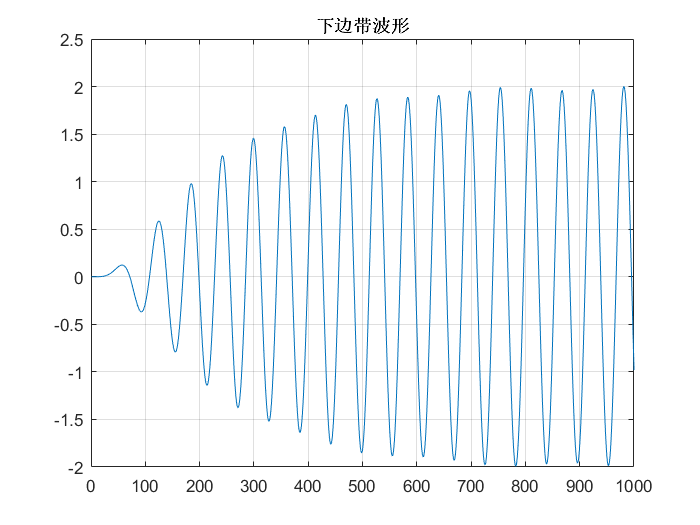
圖注：下邊帶信號波形

圖注：上邊帶信號波形

• 兩個邊帶的波形基本一致，不過可以看到上邊帶信號頻率明顯比下邊帶頻率要高，且反相

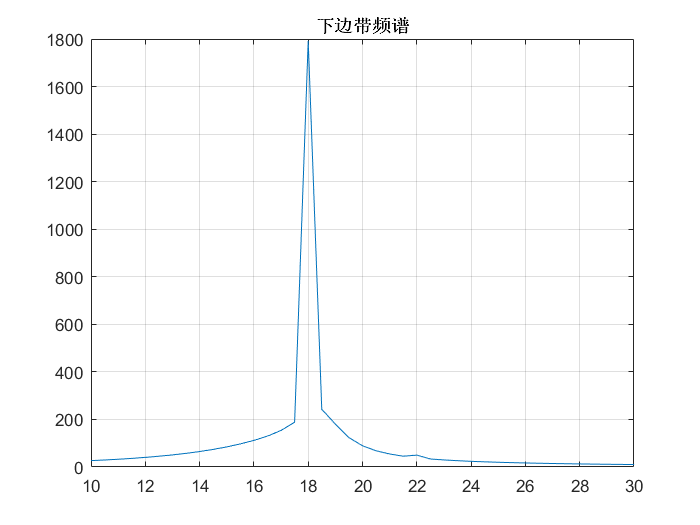
圖注：下邊帶信號頻譜

圖注：上邊帶信號頻譜

• 下邊帶信號頻譜： 主要頻率成分集中在18Hz處，上邊帶基本被濾除
• 上邊帶信號頻譜： 主要頻率成分集中在22Hz處，下邊帶基本被濾除

小結： 通過把兩個信號直接相乘來產生DSB信號，這種調制會把基帶信號的頻譜搬移到載波信號的頻譜附近，形成對稱的上下邊帶，所以從信息傳輸的角度考慮，僅需要任一邊帶就夠了，所以通過適當的低通濾波器取得下邊帶，適當的高通濾波器取得上邊帶。這里原本的濾波器采用Butterworth濾波器的設計方式，但由于過渡帶不夠窄，即不夠陡峭，總是會殘留一部分邊帶，再經過查閱資料后選擇了過渡帶比較窄的橢圓濾波器，這樣就基本濾除了另一個邊帶。

四、基于Matlab的SSB相干解調

• 實驗代碼

%SSB信號與上面SSB調制過程的信號一致
%Demodulation SSB
coherent_carrier=Sc;%相干載波與輸入載波一致
mul_LSSB_cc=coherent_carrier.*LSSB;%相干載波與下邊帶相乘
mul_USSB_cc=coherent_carrier.*USSB;%相干載波與下邊帶相乘

figure(4);
plot(mul_LSSB_cc);grid on;%顯示相干載波與下邊帶相乘后的波形
title('mul_LSSB_cc');
set(gca,'xlim',[500,2000]);
figure(5);
plot(mul_USSB_cc);grid on;%顯示相干載波與上邊帶相乘后的波形
title('mul_USSB_cc');
set(gca,'xlim',[500,2000]);

spec_LSSB_cc=fft(mul_LSSB_cc,2*Fs);%對相干載波與下邊帶相乘后的信號做FFT
spec_USSB_cc=fft(mul_USSB_cc,2*Fs);%對相干載波與上邊帶相乘后的信號做FFT

mag_LSSB_cc=abs(spec_LSSB_cc);%求頻響幅度
mag_USSB_cc=abs(spec_USSB_cc);
fdssb=(0:2*Fs-1)./2;%真實頻率

figure(6);
plot(fdssb,mag_LSSB_cc);grid on;%顯示相干載波與下邊帶相乘后的波形頻譜
title('DLSSB Spectrum');
set(gca,'xlim',[0,50]);
figure(7);
plot(fdssb,mag_USSB_cc);grid on;%顯示相干載波與上邊帶相乘后的波形頻譜
title('DUSSB Spectrum');
set(gca,'xlim',[0,50]);

%pass the LPF
LPF_LSSB=filter(BL,AL,mul_LSSB_cc);
%把相干載波與下邊帶相乘后的信號通過LPF
LPF_USSB=filter(BL,AL,mul_USSB_cc);
%把相干載波與上邊帶相乘后的信號通過LPF

figure(8);
plot(LPF_LSSB);grid on;%顯示相干載波與下邊帶相乘后信號經過LPF后的波形
title('LPF_LSSB');
set(gca,'xlim',[500,2000]);
figure(9);
plot(LPF_USSB);grid on;%顯示相干載波與上邊帶相乘后信號經過LPF后的波形
title('LPF_USSB');
set(gca,'xlim',[500,2000]);

spec_LPF_LSSB=fft(LPF_LSSB,2*Fs);
%對相干載波與下邊帶相乘后信號經過LPF后的信號做FFT
spec_LPF_USSB=fft(LPF_USSB,2*Fs);
%對相干載波與上邊帶相乘后信號經過LPF后的信號做FFT

mag_LPF_LSSB=abs(spec_LPF_LSSB);%求頻響幅度
mag_LPF_USSB=abs(spec_LPF_USSB);

figure(10);
plot(fdssb,mag_LPF_LSSB);grid on;
%顯示相干載波與下邊帶相乘后信號經過LPF后的波形頻譜
title('DLSSB Spectrum');
set(gca,'xlim',[0,50]);
figure(11);
plot(fdssb,mag_LPF_USSB);grid on;
%顯示相干載波與上邊帶相乘后信號經過LPF后的波形頻譜
title('DUSSB Spectrum');
set(gca,'xlim',[0,50]);
figure(12);
plot(Sm);grid on;
title('msg sign');
set(gca,'xlim',[500,2000]);

圖注：相干載波與LSB相乘后的信號波形
圖注：相干載波與LSB相乘后的信號頻譜

• 相干載波與LSB信號相乘后的波形頻譜在20-18=2Hz處有一個信號，在18+20=38Hz處也有一個信號，符合DSB調制的規律

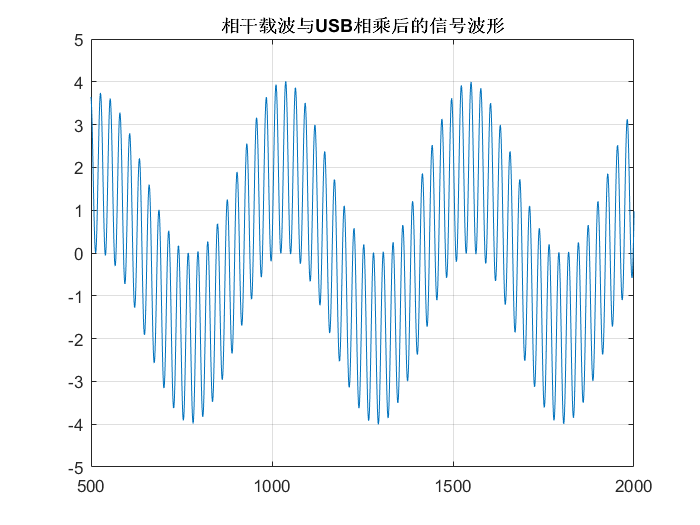
圖注：相干載波與USB相乘后的信號波形
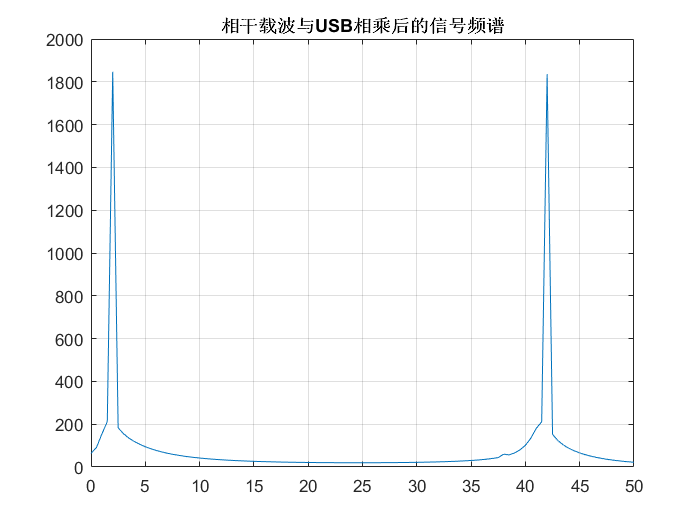
圖注：相干載波與USB相乘后的信號頻譜

• 相干載波與USB信號相乘后的波形頻譜在-20-(-22)=2Hz處有一個信號，在20+22=42Hz處也有一個信號，符合DSB調制的規律。對比上面相干載波與LSB信號相乘后的波形發現，在2Hz處都有一個相同幅值的信號。

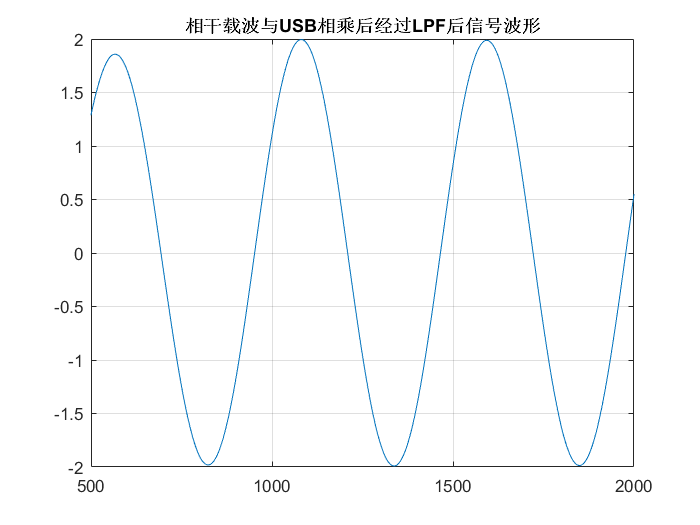
圖注：相干載波與LSB/USB相乘后經過LPF的信號波形

• 相干載波與LSB和USB信號相乘后經過LPF的波形是基本一致的

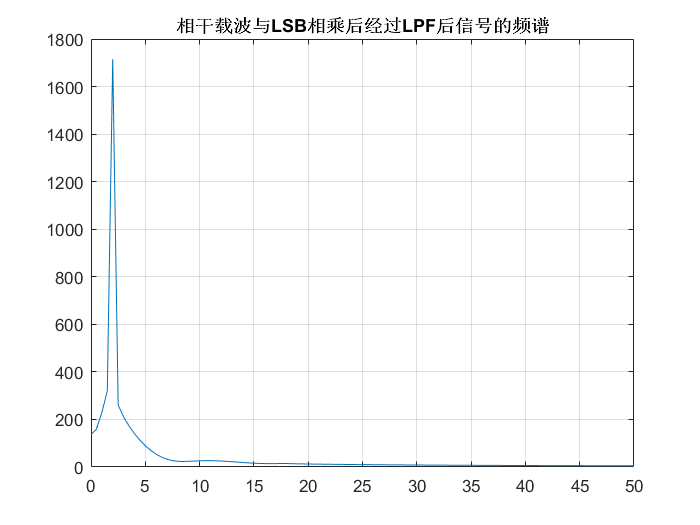
圖注：相干載波與LSB/USB相乘后經過LPF的信號頻譜

• 相干載波與LSB和USB信號相乘后經過LPF的信號頻譜是基本一致的

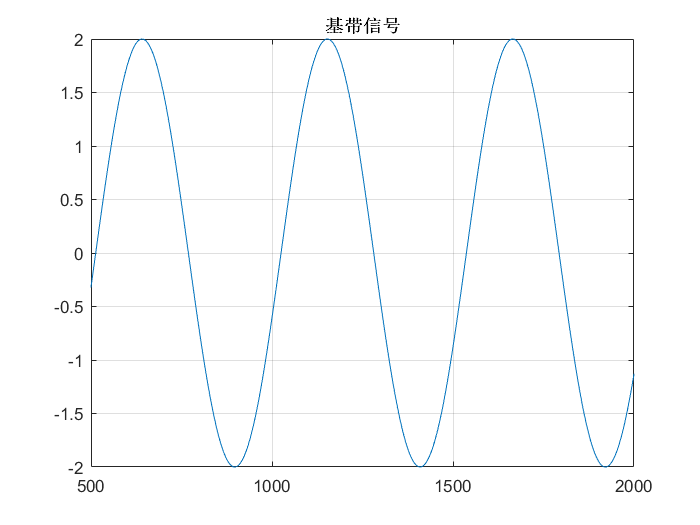
圖注：基帶信號波形

• 相干載波與LSB和USB信號相乘后經過LPF的信號與基帶信號基本一致的，說明用上邊帶或下邊帶都可以解調出基帶信號

五、基于Simulink的SSB帶加性噪聲的相干解調(下邊帶)

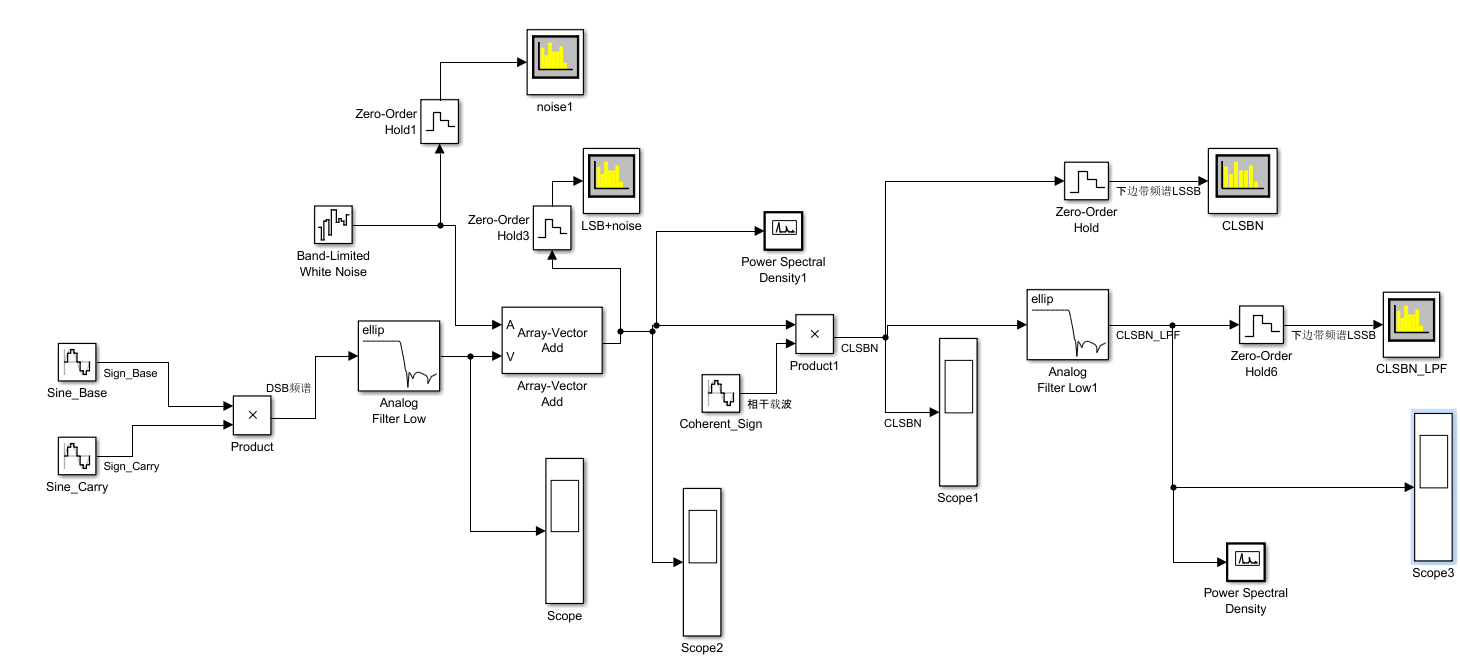
圖注：基于Simulink的SSB帶加性噪聲的相干解調模塊圖

模塊結構:

• 輸入： 一個2Hz的正弦基帶信號和一個20Hz的正弦載波信號，其中基帶信號為\(2sin(4\pi)\),載波信號為\(2sin(40\pi)\)
• 邊帶濾波器： 采用的是橢圓模擬濾波器，過渡帶比較窄。其中低通濾波器的通帶邊界頻率為20-2=18Hz，濾波器的通帶最大衰減均為0.1dB，阻帶最小衰減均為80dB
• 加性噪聲： 直接加噪聲功率為0.01的帶限白噪聲，就不用帶通濾波器了
• 相干載波： \(2sin(40\pi)\)與輸入時的載波信號同頻同相
• 低通濾波器 ： 通帶邊界頻率為2Hz的橢圓模擬低通濾波器

整體上和上面的SSB調制所用的信號和濾波器一樣

圖注：帶限白噪聲頻譜
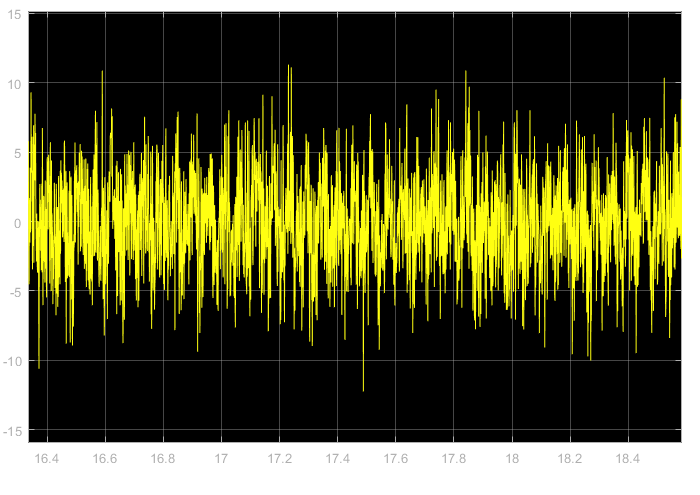
圖注：下邊帶LSB加上帶限白噪聲時域波形
圖注：下邊帶LSB加上帶限白噪聲的頻譜

• 可以看到新的信號在原來LSB頻譜上多了很多的噪聲頻譜分量

圖注：下邊帶LSB加上帶限白噪聲后與相干載波相乘的波形
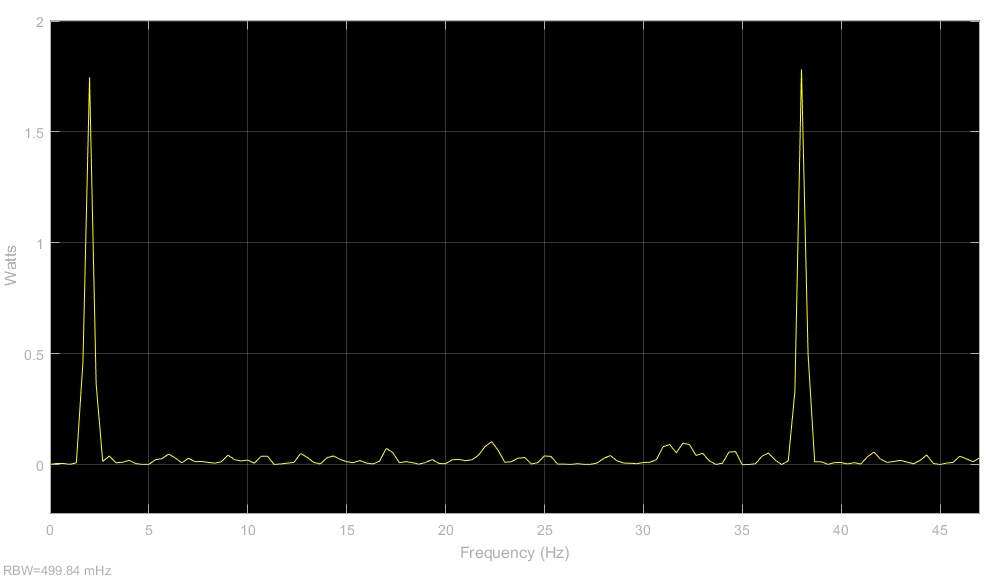
圖注：下邊帶LSB加上帶限白噪聲后與相干載波相乘的波形頻譜

• 可以看到下邊帶LSB加上帶限白噪聲后與相干載波相乘的波形頻譜在20-18=2Hz處和20+18=38Hz處都有幅度較大頻譜分量和上面無噪聲時的情況一樣。

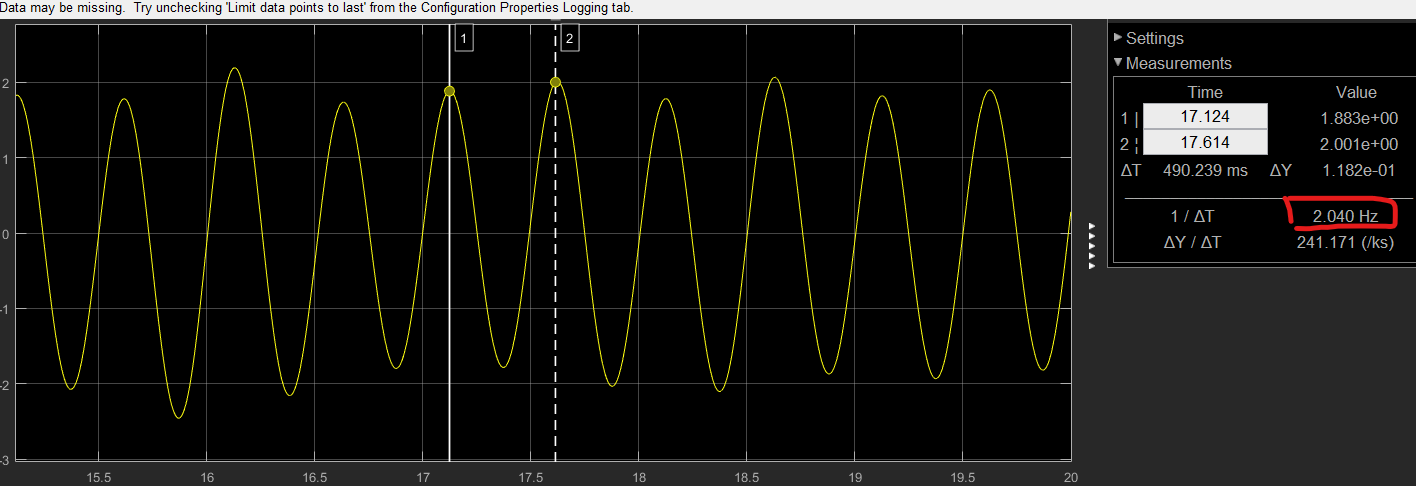
圖注：相干解調后的信號經過LPF后的信號波形

• 可以看到整體上與原基帶信號相比，幅度上會有一些畸變，頻率基本一樣，為2Hz

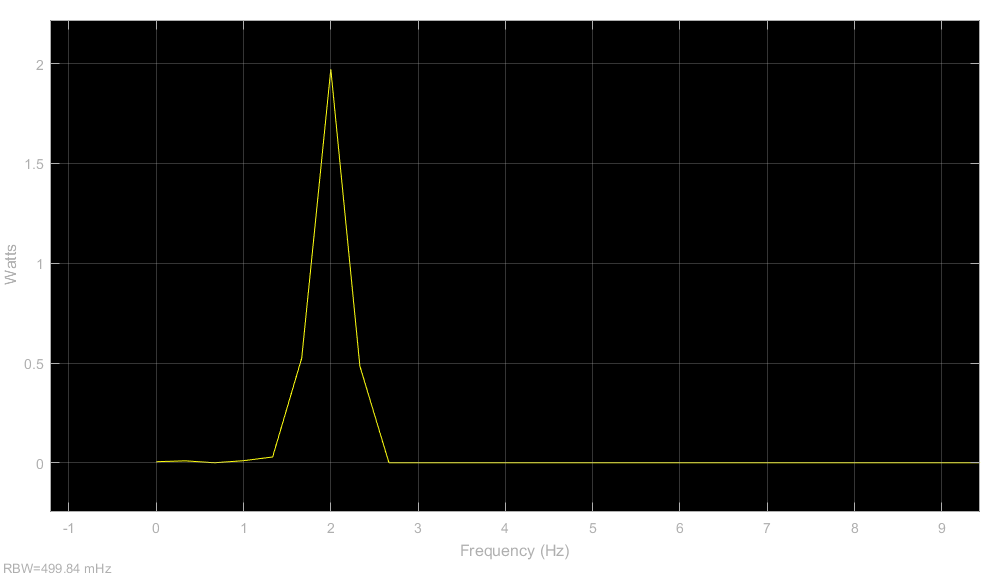
圖注：相干解調后的信號經過LPF后的信號頻譜

• 可以看到，經過LPF后的信號頻譜的主要分量就集中在2Hz處，也就是說可以解調出基帶信號

四、實驗總結

?本次實驗學習了采用濾波法實現SSB信號的調制與解調，在仿真過程中遇到許多的問題，不過通過查閱資料，詢問老師和同學，最終得到了解決，現總結如下。
?在用Simulink仿真調制與解調過程時，需要分為兩個模塊，一個為調制模塊，另一個為解調模塊。為了確認上下邊帶是否真的同時可以恢復基帶信號，所以我就對兩個邊帶同時進行調制與解調，把DSB信號通過低通濾波器得到下邊帶，通過高通濾波器得到上邊帶，然后分別與相干載波相乘后通過LPF，最后進行對比發現上下邊帶均能恢復基帶信號。在仿真過程中會遇到顯示上的問題，需要信號采樣時間間隔保持一致，在那個頻譜分析儀前還要加個零階保持器，采樣間隔需要和前面信號的一致。在做濾波器設計時，最先使用的巴特沃斯濾波器，由于過渡帶比較寬，在進行邊帶濾波時，總會殘留一些邊帶，所以最后選擇了邊帶窄的橢圓濾波器，實現了比較好的邊帶濾波效果。 而matlab代碼的仿真基本思路是一樣的。
?在用Simulink做SSB帶加性噪聲的仿真調制過程中，因為在實際中，已調信號在傳輸過程中總會受到噪聲干擾，所以只仿真了解調過程。按照書本上的原理，加性噪聲為高斯白噪聲，然后經過BPF后進行相干解調，但由于版本問題，沒有高斯白噪聲模塊，所以我這里就直接用了帶限白噪聲，相當于高斯白噪聲通過BPF后的帶限白噪聲，然后進行相干解調，解調出來的信號，與基帶信號相比，會有不少的畸變，當然因為實際情況更為復雜，所以我的仿真模塊一些參數的設計并不能滿足實際，所以這是我需要提升的。