參數化(parameterization)
建立一個三角網格曲面的參數化意味著找到一個坐標集合(ui,vi)與每一個頂點對應,坐標集合應該滿足如下的條件:參數化之后的面不會自交。
幾種不同的參數化方法:
重心映射( Barycentric Mapping)
重心映射是比較常見的三角網格參數化方法。給定一個三角網格曲面與圓盤(disk)同胚,如果邊界頂點參數化之后的點連成一個凸多邊形,內部頂點參數化之后的點是它1-鄰域的頂點參數化之后坐標的凸組合,這樣的參數化方法就是一種有效的參數化方法(不會自交)。

拉普拉斯算子
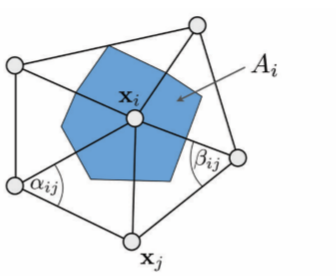
拉普拉斯算子衡量函數的規則性,例如,線性函數的;拉普拉斯算子為0,因此,極小化u,v的拉普拉斯算子可以得到光滑的參數化坐標,話句話說,極小化了參數化之后的扭曲。用離散微分幾何的拉普拉斯算子可以計算ai,j
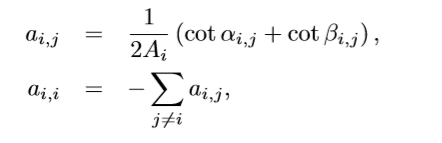




 浙公網安備 33010602011771號
浙公網安備 33010602011771號