1. 思維導圖

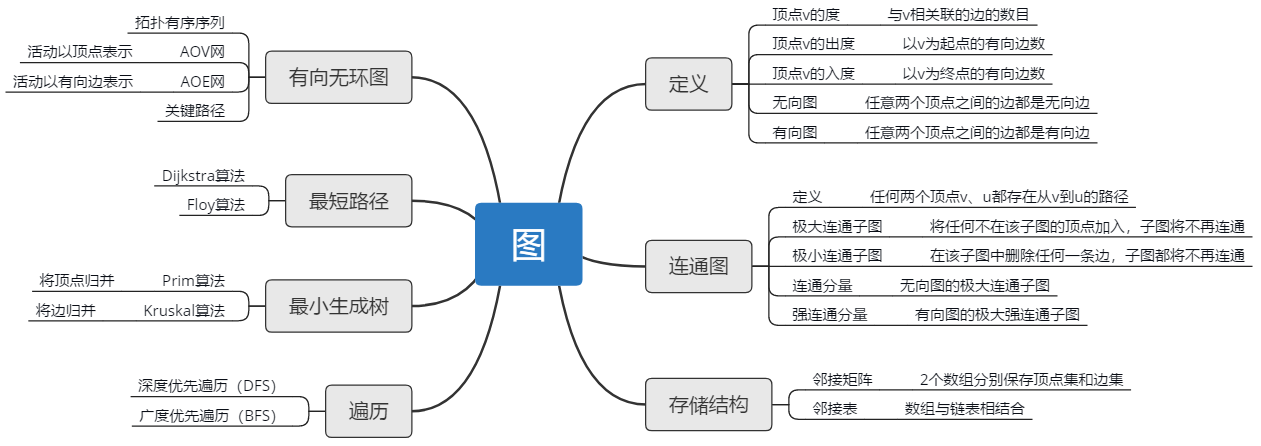
2. 概念筆記

(1) 深度優先遍歷（DFS）

a. 訪問頂點v
b. 依次從v的未被訪問的鄰接點出發，對圖進行深度優先遍歷；直至圖中和v有路徑相通的頂點都被訪問
c. 若此時圖中尚有頂點未被訪問，則從一個未被訪問的頂點出發，重新進行深度優先遍歷，直到圖中所有頂點均被訪問過為止

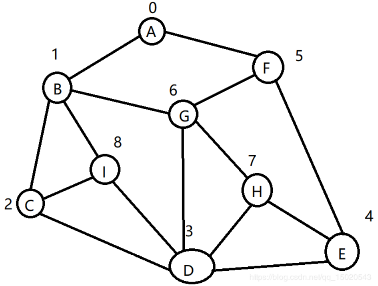
(2) 廣度優先遍歷（BFS）

a. 從圖中某個頂點v出發，訪問v
b. 依次訪問v的各個未被訪問過的鄰接點
c. 分別從這些鄰接點出發依次訪問他們的鄰接點
d. 重復步驟c，直至所有已被訪問的頂點的鄰接點都被訪問到

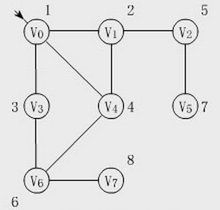
(3) Prim 算法

a. 以某一個點開始，尋找當前該點可以訪問的所有的邊
b. 在已經尋找的邊中發現最小邊，這個邊必須有一個點還沒有訪問過，將還沒有訪問的點加入集合，記錄添加的邊
c. 尋找當前集合可以訪問的所有邊，重復 b 的過程，直到沒有新的點可以加入

(4) Kruskal 算法

a. 設一個有n個頂點的連通網絡為 G（V,E），最初先構造一個只有 n 個頂點，沒有邊的非連通圖 T，圖中每個頂點自成一個連通分量
b. 當在E中選擇一條具有最小權值的邊時，若該邊的兩個頂點落在不同的連通分量上，則將此邊加入到 T 中；否則重新選擇一條權值最小的邊
c. 如此重復下去，直到所有頂點在同一個連通分量上為止

(5) Dijkstra 算法

a. 遍歷與結點1相連的所有結點，找到距離最近的一個，把這個結點標記為訪問過，并更新最短路徑
b. 遍歷最短路徑包含的點相連的節點，找到距離最近的加入最短路徑，并且標記為訪問過
c. 重復 b 步驟
總結：先遍歷一遍還沒有在最短路徑中的點，選出一個距離最近的點，把它加入到最短路徑中并更新，直到所有的點都加入到最短路徑中。