1 導引

我們在上一篇博客《學習理論：預測器-拒絕器多分類棄權學習》中介紹了棄權學習^[1]的基本概念和方法，其中包括了下列針對多分類問題的單階段預測器-拒絕器棄權損失\(L_{\text{abst}}\)：

其中\((x, y)\in \mathcal{X}\times \mathcal{Y}\)（標簽\(\mathcal{Y} = \{1, \cdots, n\}\)（\(n\geqslant 2\)）），\((h, r)\in \mathcal{H}\times\mathcal{R}\)為預測器-拒絕器對（\(\mathcal{H}\)和\(\mathcal{R}\)為兩個從\(\mathcal{X}\)到\(\mathbb{R}\)的函數構成的函數族），\(\text{h}(x) = \underset{y\in \mathcal{Y}}{\text{arg max}}\space {h(x)}_y\)直接輸出實例\(x\)的預測標簽。為了簡化討論，在后文中我們假設\(c\in (0, 1)\)為一個常值花費函數。

設\(\mathcal{l}\)為在標簽\(\mathcal{Y}\)上定義的0-1多分類損失的代理損失，則我們可以在此基礎上進一步定義棄權代理損失\(L\)：

其中\(\psi\)是非遞減函數，\(\phi\)是非遞增輔助函數（做為\(z \mapsto \mathbb{I}_{z \leqslant 0}\)的上界），\(\alpha\)、\(\beta\)為正常量。下面，為了簡便起見，我們主要對\(\phi(z) = \exp(-z)\)進行分析，盡管相似的分析也可以應用于其它函數\(\phi\)。

在上一篇博客中，我們還提到了單階段代理損失滿足的\((\mathcal{H}, \mathcal{R})\)-一致性界：

定理 1 單階段代理損失的\((\mathcal{H}, \mathcal{R})\) - 一致性界 假設\(\mathcal{H}\)是對稱與完備的。則對\(\alpha=\beta\)，\(\mathcal{l} = \mathcal{l}_{\text{mae}}\)，或者\(\mathcal{l} = \mathcal{l}_{\rho}\)與\(\psi(z) = z\)，或者\(\mathcal{l} = \mathcal{l}_{\rho - \text{hinge}}\)與\(\psi(z) = z\)，有下列\((\mathcal{H}, \mathcal{R})\) - 一致性界對\(h\in \mathcal{H}, r\in \mathcal{R}\)和任意分布成立：

其中對\(\mathcal{l} = \mathcal{l}_{\text{mae}}\)取\(\Gamma (z) = \max\{2n\sqrt{z}, nz\}\)；對\(\mathcal{l}=\mathcal{l}_{\rho}\)取\(\Gamma (z) = \max\{2\sqrt{z}, z\}\)；對\(\mathcal{l} = \mathcal{l}_{\rho - \text{hinge}}\)取\(\Gamma (z) = \max\{2\sqrt{nz}, z\}\)。

不過，在上一篇博客中，我們并沒有展示單階段代理損失的\((\mathcal{H}, \mathcal{R})\)-一致性界的詳細證明過程，在這片文章里我們來看該如何對該定理進行證明（正好我導師也讓我仔細看看這幾篇論文^[1][2]中相關的分析部分，并希望我掌握單階段方法的證明技術）。

2 一些分析的預備概念

我們假設帶標簽樣本\(S=((x_1, y_1), \cdots, (x_m, y_m))\)獨立同分布地采自\(p(x, y)\)。則對于目標損失\(L_{\text{abst}}\)和代理損失\(L\)而言，可分別定義\(L_{\text{abst}}\)-期望棄權損失\(R_{L_{\text{abst}}}(h, r)\)（也即目標損失函數的泛化誤差）和\(L\)-期望棄權代理損失\(R_{L}(h, r)\)（也即代理損失函數的泛化誤差）如下：

設\(R_{{L}_{\text{abst}}}^*(\mathcal{H}, \mathcal{R}) = \inf_{h\in \mathcal{H}, r\in \mathcal{R}}R_{L_{\text{abst}}}(\mathcal{H}, \mathcal{R})\)和\(R_{L}^{*}(\mathcal{H}, \mathcal{R}) = \inf_{h\in \mathcal{H}, r\in \mathcal{R}}R_{L}(\mathcal{H}, \mathcal{R})\)分別為\(R_{L_{\text{abst}}}\)和\(R_L\)在\(\mathcal{H}\times \mathcal{R}\)上的下確界。
為了進一步簡化后續的分析，我們根據概率的乘法規則將\(R_L(h, r)\)寫為：

我們稱其中內層的條件期望項為代理損失\(L\)的條件風險（conditional risk）（也稱為代理損失\(L\)的pointwise風險^[2]），由于在其計算過程中\(y\)取期望取掉了，因此該項只和\(h\)、\(r\)、\(x\)相關，因此我們將其記為\(C_L(h, r, x)\)：

我們用\(C^*_L(\mathcal{H}, \mathcal{R}, x) = \inf_{h\in \mathcal{H}, r\in \mathcal{R}} C_L(h, r, x)\)來表示假設類最優（best-in-class） 的\(L\)的條件風險。同理，我們用\(C_{L_{\text{abst}}}\)來表示目標損失\(L_{\text{abst}}\)的條件風險，并用\(C^*_{L_{\text{abst}}}\)來表示假設類最優的\(L_{\text{abst}}\)的條件風險。

根據\(R_{L}^*(\mathcal{H}, \mathcal{R})\)和\(C^*_L(\mathcal{H}, \mathcal{R}, x)\)，我們可以表示出可最小化差距（minimizability gap）：

\(M_{L_{\text{abst}}}\)的表示同理。

于是，我們可以對要證明的\((\mathcal{H}, \mathcal{R})\)-一致性界進行改寫：

其中\(R_{L_{\text{abst}}}(h, r)\)和\(R_L(h, r)\)分別為\(\mathbb{E}_{p(x)}\left[C_{L_{\text{abst}}}(h, r, x)\right]\)和\(\mathbb{E}_{p(x)}\left[C_{L}(h, r, x)\right]\)，于是上述不等式即為

我們將上述不等式兩邊的被取期望的項簡記為\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x)\)和\(\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x)\)，其中\(\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x)\)被稱為校準差距（calibration gap）。由于按定義\(\Gamma(\cdot)\)是凹函數，由Jensen不等式有：

于是，若我們能證明下述不等式，則原不等式得證：

我們后面將會看到，\((\mathcal{H}, \mathcal{R})\)-一致性界的證明過程中重要的一步即是證明\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x)\)能被\(\Gamma \left(\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x)\right)\)界定。

3 \(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x)\)的表示

我們先來看\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x) = C_{L_{\text{abst}}}(h, r, x) - C^*_{L_{\text{abst}}}(\mathcal{H}, \mathcal{R}, x)\)如何表示。根據定義，我們有：

由于是關于\(y\)的條件期望，上式最后一行中只需要對\(\mathbb{I}_{\text{h}(x) \neq y}\)進行加權求和即可。為了進一步對\(C_{L_{\text{abst}}}(h, r, x)\)進行表示，我們需要對\(r(x)\)的符號情況進行分類討論：

1. \(r(x) > 0\)：此時\(C_{L_{\text{abst}}}(h, r, x) = \sum_{y\in \mathcal{Y}}p(y\mid x) \mathbb{I}_{\text{h}(x) \neq y} = 1 - p(\text{h}(x)\mid x)\)。
2. \(r(x) \leqslant 0\)：此時\(C_{L_{\text{abst}}}(h, r, x) = c\)。

接下來我們來看\(C^*_{L_{\text{abst}}}\)如何表示。我們假設拒絕函數集\(\mathcal{R}\)是完備的（也即對任意\(x\in \mathcal{X}, \{r(x): r\in \mathcal{R}\} = \mathbb{R}\)），那么\(\mathcal{R}\)也是棄權正規的（也即使得對任意\(x\in \mathcal{X}\)，存在\(r_1, r_2\in \mathcal{R}\)滿足\(r_1(x) > 0\)與\(r_2(x) \leqslant 0\)）。于是我們有

我們假設\(\mathcal{H}\)是對稱的且完備的（具體定義參見博客《學習理論：預測器-拒絕器多分類棄權學習》），則我們有\(\left\{\text{h}(x): h\in \mathcal{H}\right\} = \mathcal{Y}\)，于是

為了進一步對\(C^*_{L_{\text{abst}}}(\mathcal{H}, \mathcal{R}, x)\)進行表示，我們需要對\(\max_{y\in \mathcal{Y}}p(y\mid x)\)和\((1 - c)\)的大小比較情況進行分類討論：

1. \(\max_{y\in \mathcal{Y}}p(y\mid x) > 1 - c\)：此時\(C^*_{L_{\text{abst}}}(\mathcal{H}, \mathcal{R}, x) = 1 - \max_{y\in \mathcal{Y}}p(y\mid x)\)。
2. \(\max_{y\in \mathcal{Y}}p(y\mid x) \leqslant 1 - c\)：此時\(C^*_{L_{\text{abst}}}(\mathcal{H}, \mathcal{R}, x) = c\)。

于是，我們有：

4 \(\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x)\)的表示

4.1 分類討論的準備

接下來我們來看\(\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x) = C_L(h, r, x) - C^*_L(\mathcal{H}, \mathcal{R}, x)\)如何表示。根據定義，若\(\alpha = \beta\)，\(\phi(z) = \exp(-z)\)，我們有：

由于是關于\(y\)的條件期望，上式最后一行中只需要對\(\mathcal{l}(h, x, y)\)進行加權求和即可。在后文中我們將會針對下列三種不同的\(\mathcal{l}\)函數以及\(\psi(z)\)的選擇情況來分別對\(C_L(h, r, x)\)進行討論：

1. \(\mathcal{l} = \mathcal{l}_{\text{mae}}\)，\(\psi(z) = z\)；
2. \(\mathcal{l} = \mathcal{l}_{\rho}\)，\(\psi(z) = z\)；
3. \(\mathcal{l} = \mathcal{l}_{\rho-\text{hinge}}\)，\(\psi(z) = nz\)。

注 這三種不同\(\mathcal{l}\)的定義參見博客《學習理論：預測器-拒絕器多分類棄權學習》），我在這里把它們的定義貼一下：

• 平均絕對誤差損失：\(\mathcal{l}_{\text{mae}}(h, x, y) = 1 - \frac{e^{{h(x)}_y}}{\sum_{y^{\prime}\in \mathcal{Y}}e^{{h(x)}_{y^{\prime}}}}\)；
• 約束\(\rho\)-合頁損失：\(\mathcal{l}_{\rho-\text{hinge}}(h, x, y) = \sum_{y^{\prime}\neq y}\phi_{\rho-\text{hinge}}(-{h(x)}_{y^{\prime}}), \rho > 0\)，其中\(\phi_{\rho-\text{hinge}}(z) = \max\{0, 1 - \frac{z}{\rho}\}\)為\(\rho\)-合頁損失，且約束條件\(\sum_{y\in \mathcal{Y}}{h(x)}_y=0\)。
• \(\rho\)-間隔損失：\(\mathcal{l}_{\rho}(h, x, y) = \phi_{\rho}({\rho_h (x, y)})\)，其中\(\rho_{h}(x, y) = h(x)_y - \max_{y^{\prime} \neq y}h(x)_{y^{\prime}}\)是置信度間隔，\(\phi_{\rho}(z) = \min\{\max\{0, 1 - \frac{z}{\rho}\}, 1\}, \rho > 0\)為\(\rho\)-間隔損失。

4.2 \(\mathcal{l} = \mathcal{l}_{\text{mae}}\)，\(\psi(z) = z\)

在這種情況下\(C_L(h, r, x)\)可以表示為：

其中\(s_h(x, y) = \frac{e^{{h(x)}_y}}{\sum_{y^{\prime}\in \mathcal{Y}}e^{{h(x)}_{y^{\prime}}}}\)。

于是

由于假設了\(\mathcal{H}\)是對稱的與完備的，我們有

注 實際上，對任意\(h\in \mathcal{H}\)，有：

\[\begin{aligned} &\sum_{y\in \mathcal{Y}}p(y\mid x) \left(1 - s_h(x, y)\right) - \left(1 - \max_{y\in \mathcal{Y}}p\left(y\mid x\right)\right) \\ &= \max_{y\in \mathcal{Y}} p(y\mid x) - \sum_{y\in \mathcal{Y}}p(y\mid x)s_h(x, y) \\ &= \max_{y\in \mathcal{Y}} p(y\mid x) - \left(p\left(\text{h}(x)\mid x\right)s_h\left(x, \text{h}(x)\right) + \sum_{y\neq \text{h}(x)}p(y\mid x)s_h(x, y)\right) \\ &\geqslant \max_{y\in \mathcal{Y}} p(y\mid x) - \left(p\left(\text{h}(x)\mid x\right)s_h\left(x, \text{h}(x)\right) + \max_{y\in \mathcal{Y}}p(y\mid x)\left(1 - s_h\left(x, \text{h}(x)\right)\right)\right) \\ &= s_h\left(x, \text{h}(x)\right)\left(\max_{y\in \mathcal{Y}}p(y\mid x) - p\left(\text{h}(x)\mid x\right)\right) \\ &\geqslant \frac{1}{n} \left(\max_{y\in \mathcal{Y}}p(y\mid x) - p\left(\text{h}(x)\mid x\right)\right) \end{aligned} \]

這個結論我們會在后面的證明中多次用到。該結論的一個推論是如果分類器\(h^*\)為貝葉斯最優分類器（也即\(p(\text{h}^*(x)\mid x) = \max_{y\in \mathcal{Y}} p(y\mid x)\)），則\(\sum_{y\in \mathcal{Y}}p(y\mid x) \left(1 - s_h(x, y)\right) - \left(1 - \max_{y\in \mathcal{Y}}p(y\mid x)\right) \geqslant 0\)，可直觀地將其理解為\(\mathbb{E}_{p(y\mid x)}\left[\mathcal{l}_{\text{mae}}\right]\)可達到其下確界。

于是

記上式中需要求極值的部分為泛函\(F(r)\)，則其泛函導數為

令\(\frac{\delta F}{\delta r(x)} = 0\)（對\(\forall x\in \mathcal{X}\)），解得\(r^*(x) = -\frac{1}{2\alpha}\log \left(\frac{1 - \max_{y\in \mathcal{Y}}p(y\mid x)}{c}\right)\)。將其代入\(F(r)\)可得：

于是

為了構建\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x)\)和\(\Gamma \left(\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x)\right)\)的不等式關系，接下來我們將會采用第3節中類似的做法，針對\(\max_{y\in \mathcal{Y}} p(y\mid x)\)與\(1 - c\)的大小比較情況與\(r(x)\)的符號情況來對\(\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x)\)進行分類討論：

1. \(\max_{y\in \mathcal{Y}} p(y\mid x) > (1 - c)\)，\(r(x) > 0\)：
   此時

   \[\begin{aligned} \Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x) &= \sum_{y\in \mathcal{Y}}p(y\mid x) \left(1 - s_h(x, y)\right)e^{\alpha r(x)} + c e^{-\alpha r(x)} - 2\sqrt{c\left(1 - \max_{y\in \mathcal{Y}}p(y\mid x)\right)} \\ &= \sum_{y\in \mathcal{Y}}p(y\mid x) \left(1 - s_h(x, y)\right)e^{\alpha r(x)} + c e^{-\alpha r(x)} - 2\sqrt{ce^{-\alpha r(x)}\left(1 - \max_{y\in \mathcal{Y}}p(y\mid x)\right)e^{\alpha r(x)}} \\ &\geqslant \sum_{y\in \mathcal{Y}}p(y\mid x) \left(1 - s_h(x, y)\right)e^{\alpha r(x)} + c e^{-\alpha r(x)} - ce^{-\alpha r(x)} - \left(1 - \max_{y\in \mathcal{Y}}p(y\mid x)\right)e^{\alpha r(x)} \\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (\text{AM-GM inequality}) \\ &\geqslant \sum_{y\in \mathcal{Y}}p(y\mid x) \left(1 - s_h(x, y)\right) - \left(1 - \max_{y\in \mathcal{Y}}p(y\mid x)\right)\\ &\geqslant \frac{1}{n} \left(\max_{y\in \mathcal{Y}}p(y\mid x) - p\left(\text{h}(x)\mid x\right)\right) \\ &= \frac{1}{n} \Delta C_{\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x) \end{aligned} \]

   （其中\(\text{AM-GM inequality}\)為算術-幾何平均值不等式）
   取\(\Gamma_1 (z) = nz\)，于是\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x) \leqslant \Gamma \left(\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x)\right)\)得證。

2. \(\max_{y\in \mathcal{Y}} p(y\mid x) \leqslant (1 - c)\)，\(r(x) > 0\)：
   此時

   \[ \begin{aligned} \Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x) &= \sum_{y\in \mathcal{Y}}p(y\mid x) \left(1 - s_h(x, y)\right)e^{\alpha r(x)} + c e^{-\alpha r(x)} - 2\sqrt{c\left(1 - \max_{y\in \mathcal{Y}}p(y\mid x)\right)} \\ & \geqslant \underbrace{\sum_{y\in \mathcal{Y}}p(y\mid x) \left(1 - s_h\left(x, y\right)\right)}_{\geqslant c}e^{\alpha r(x)} + c e^{-\alpha r(x)} - 2\sqrt{c\left(\sum_{y\in \mathcal{Y}}p(y\mid x)\left(1 - s_h(x, y)\right)\right)} \\ & \geqslant \sum_{y\in \mathcal{Y}}p(y\mid x) \left(1 - s_h(x, y)\right) + c - 2\sqrt{c\left(\sum_{y\in \mathcal{Y}}p(y\mid x)\left(1 - s_h(x, y)\right)\right)} \\ &= \left(\sqrt{\sum_{y\in \mathcal{Y}}p(y\mid x) \left(1 - s_h(x, y)\right)} - \sqrt{c}\right)^2 \\ &= \left(\frac{\sum_{y\in \mathcal{Y}}p(y\mid x) \left(1 - s_h(x, y)\right) - c}{\sqrt{\sum_{y\in \mathcal{Y}}p(y\mid x) \left(1 - s_h(x, y)\right)} + \sqrt{c}}\right)^2 \\ &\geqslant \left(\frac{\sum_{y\in \mathcal{Y}}p(y\mid x) \left(1 - s_h(x, y)\right) - \left(1 - \max_{y\in \mathcal{Y}}p(y\mid x)\right) + \left(1 - \max_{y\in \mathcal{Y}}p(y\mid x) - c\right)}{2}\right)^2 \\ &\geqslant \left(\frac{\frac{1}{n} \left(\max_{y\in \mathcal{Y}}p(y\mid x) - p\left(\text{h}(x)\mid x\right)\right) + \frac{1}{n}\left(1 - \max_{y\in \mathcal{Y}}p(y\mid x) - c\right)}{2}\right)^2 \\ &= \frac{1}{4n^2}\left(1 - c - p\left(\text{h}(x)\mid x\right)\right)^2 \\ &= \frac{\Delta C_{\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x)^2}{4n^2} \end{aligned} \]

   取\(\Gamma_2 (z) = 2n\sqrt{z}\)，于是\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x) \leqslant \Gamma \left(\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x)\right)\)得證。

3. \(\max_{y\in \mathcal{Y}} p(y\mid x) \leqslant (1 - c)\)，\(r(x) \leqslant 0\)：
   由于此時\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x) = 0\)，因此\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x) \leqslant \Gamma\left(\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x)\right)\)對任意\(\Gamma \geqslant 0\)成立。

4. \(\max_{y\in \mathcal{Y}} p(y\mid x) > (1 - c)\)，\(r(x) \leqslant 0\)：
   此時

   \[ \begin{aligned} \Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x) &= \sum_{y\in \mathcal{Y}}p(y\mid x) \left(1 - s_h(x, y)\right)e^{\alpha r(x)} + c e^{-\alpha r(x)} - 2\sqrt{c\left(1 - \max_{y\in \mathcal{Y}}p(y\mid x)\right)} \\ &\geqslant \left(1 - \max_{y\in \mathcal{Y}}p(y\mid x)\right)\underbrace{e^{\alpha r(x)}}_{\leqslant 1} + c \underbrace{e^{-\alpha r(x)}}_{\geqslant 1} - 2\sqrt{c\left(1 - \max_{y\in \mathcal{Y}}p(y\mid x)\right)} \\ &\geqslant 1 - \max_{y\in \mathcal{Y}}p(y\mid x) + c - 2\sqrt{c\left(1 - \max_{y\in \mathcal{Y}}p(y\mid x)\right)} \\ &= \left(\sqrt{1 - \max_{y\in \mathcal{Y}}p(y\mid x)} - \sqrt{c}\right)^2 \\ &= \left(\frac{1 - \max_{y\in \mathcal{Y}}p(y\mid x) - c}{\sqrt{1 - \max_{y\in \mathcal{Y}}p(y\mid x)} + \sqrt{c}}\right)^2 \\ &\geqslant \left(\frac{\max_{y\in \mathcal{Y}}p(y\mid x) - 1 + c}{2}\right)^2 \\ &= \frac{\Delta C_{\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x)^2}{4} \end{aligned} \]

   取\(\Gamma_3 (z) = 2\sqrt{z}\)，于是\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x) \leqslant \Gamma \left(\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x)\right)\)得證。

綜上所述，若取\(\Gamma(z) = \max\{\Gamma_1(z), \Gamma_2(z), \Gamma_3(z)\} = \max\{2n\sqrt{z}, nz\}\)，則恒有\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x) \leqslant \Gamma \left(\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x)\right)\)。于是\(\mathcal{l} = \mathcal{l}_{\text{mae}}\)，\(\psi(z) = z\)時單階段代理損失的\((\mathcal{H}, \mathcal{R})\)-一致性界得證。

4.3 \(\mathcal{l} = \mathcal{l}_{\rho}\)，\(\psi(z) = z\)

在這種情況下\(C_L(h, r, x)\)可以表示為：

其中\(\rho_h(x, y) = h(x)_y - \max_{y^{\prime}\neq y}h(x)_{y^{\prime}}\)為間隔。

而

于是\(C_L(h, r, x)\)可進一步寫為：

由于假設了\(\mathcal{H}\)是對稱的與完備的，我們有

注 實際上，對任意\(h\in \mathcal{H}\)，有：

\[\begin{aligned} &\left(1 - p(\text{h}(x)\mid x)\min\left\{1, \frac{\rho_h(x, \text{h}(x))}{\rho}\right\}\right) - \left(1 - \max_{y\in \mathcal{Y}}p\left(y\mid x\right)\right) \\ &= \max_{y\in \mathcal{Y}} p(y\mid x) - p\left(\text{h}(x)\mid x\right)\min \left\{1, \frac{\rho_h\left(x, \text{h}(x)\right)}{\rho}\right\} \\ &\geqslant \max_{y\in \mathcal{Y}}p\left(y\mid x\right) - p\left(\text{h}(x)\mid x\right) \end{aligned} \]

和之前\(\mathcal{l}_{\text{mae}}\)的證明類似，這個結論我們會在后面的證明中多次用到。

于是和之前\(\mathcal{l}_{\text{mae}}\)類似，我們有

于是

為了構建\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x)\)和\(\Gamma \left(\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x)\right)\)的不等式關系，接下來我們將會采用\(\mathcal{l}_{\text{mae}}\)的證明中類似的做法，針對\(\max_{y\in \mathcal{Y}} p(y\mid x)\)與\(1 - c\)的大小比較情況與\(r(x)\)的符號情況來對\(\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x)\)進行分類討論：

1. \(\max_{y\in \mathcal{Y}} p(y\mid x) > (1 - c)\)，\(r(x) > 0\)：
   此時

   \[\begin{aligned} \Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x) &= \left(1 - p(\text{h}(x)\mid x)\min\left\{1, \frac{\rho_h(x, \text{h}(x))}{\rho}\right\}\right)e^{\alpha r(x)} + c e^{-\alpha r(x)} - 2\sqrt{c\left(1 - \max_{y\in \mathcal{Y}}p\left(y\mid x\right)\right)} \\ &\geqslant \max_{y\in \mathcal{Y}}p(y\mid x) - p(\text{h}(x)\mid x)\\ &= \Delta C_{\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x) \end{aligned} \]

   （由于證明步驟與\(\mathcal{l}_{\text{mae}}\)類似，這里對證明步驟進行了一些精簡，下面同理）
   取\(\Gamma_1 (z) = z\)，于是\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x) \leqslant \Gamma (\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x))\)得證。

2. \(\max_{y\in \mathcal{Y}} p(y\mid x) \leqslant (1 - c)\)，\(r(x) > 0\)：
   此時

   \[\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x) \geqslant \frac{1}{4}\left(1 - c - p\left(\text{h}\left(x\right)\mid x\right)\right)^2 = \frac{\Delta C_{\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x)^2}{4} \]

   取\(\Gamma_2 (z) = 2\sqrt{z}\)，于是\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x) \leqslant \Gamma (\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x))\)得證。

3. \(\max_{y\in \mathcal{Y}} p(y\mid x) \leqslant (1 - c)\)，\(r(x) \leqslant 0\)：
   由于此時\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x) = 0\)，因此\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x) \leqslant \Gamma (\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x))\)對任意\(\Gamma \geqslant 0\)成立。

4. \(\max_{y\in \mathcal{Y}} p(y\mid x) > (1 - c)\)，\(r(x) \leqslant 0\)：
   此時

   \[\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x) \geqslant \left(\frac{\max_{y\in \mathcal{Y}}p(y\mid x) - 1 + c}{2}\right)^2 = \frac{\Delta C_{\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x)^2}{4} \]

   取\(\Gamma_3 (z) = 2\sqrt{z}\)，于是\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x) \leqslant \Gamma (\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x))\)得證。

綜上所述，若取\(\Gamma(z) = \max\{\Gamma_1(z), \Gamma_2(z), \Gamma_3(z)\} = \max\{2\sqrt{z}, z\}\)，則恒有\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x) \leqslant \Gamma (\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x))\)。于是\(\mathcal{l} = \mathcal{l}_{\rho}\)，\(\psi(z) = z\)時單階段代理損失的\((\mathcal{H}, \mathcal{R})\)-一致性界得證。

4.4 \(\mathcal{l} = \mathcal{l}_{\rho-\text{hinge}}\)，\(\psi(z) = nz\)

在這種情況下\(C_L(h, r, x)\)可以表示為：

其中第二行的交換\(\sum_{y\in \mathcal{Y}}\)和\(\sum_{y^{\prime}\neq y}\)的求和順序可參照下圖進行理解（以類別數\(n = 3\)的情況為例）：

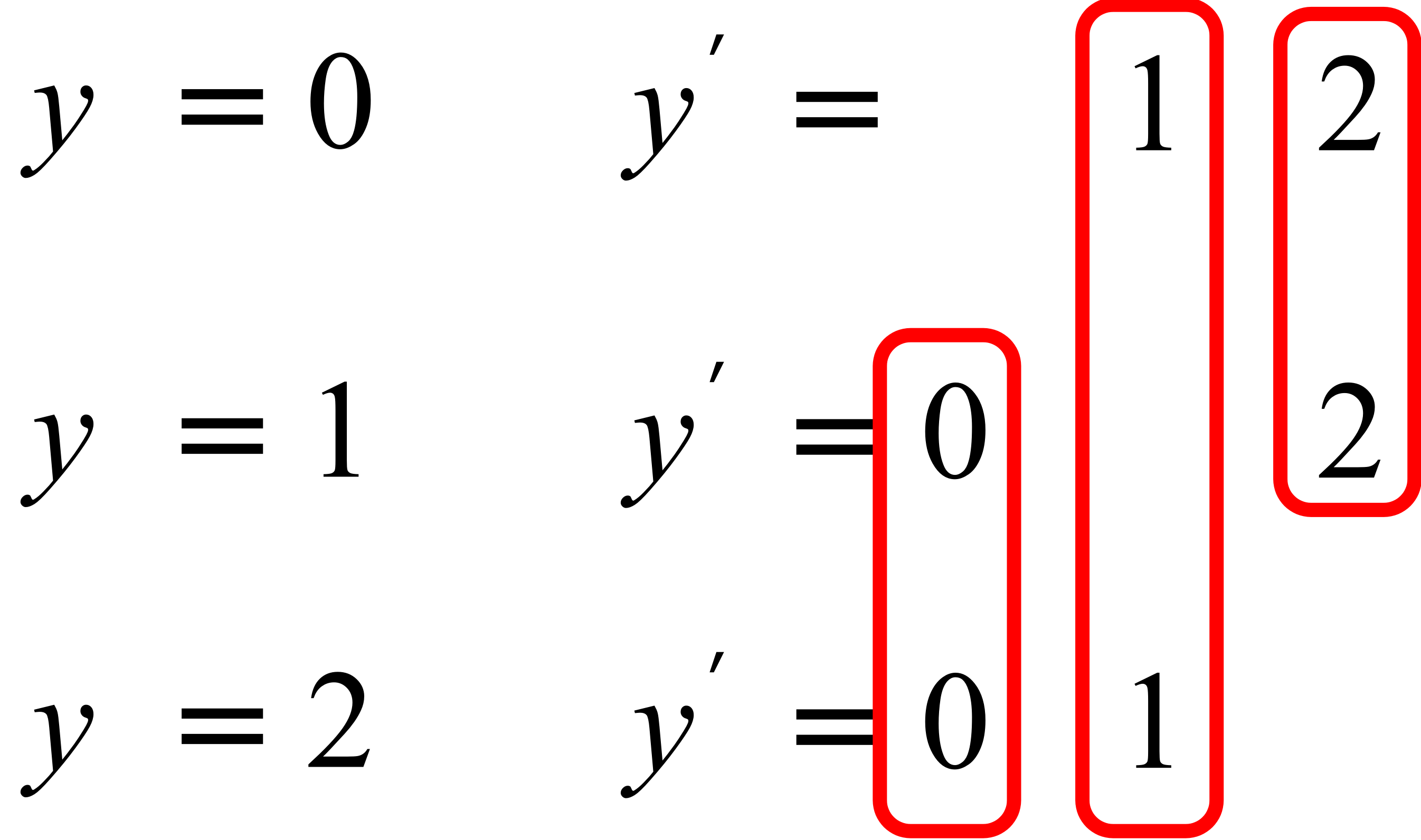
注 這種交換雙重求和順序的類似技巧我們在博客《隨機算法：蒙特卡洛和拉斯維加斯算法》分析隨機快速排序算法所做比較的期望次數時提到過，感興趣的讀者可以前去看一下。

由于假設了\(\mathcal{H}\)是對稱的與完備的，我們有

注 實際上，若取\(h_{\rho}\)使得\(h_{\rho}(x)_y = \left\{\begin{aligned} &h(x)_y\quad &\text{if } y\notin \left\{y_{\max}, \text{h}(x)\right\} \\ &-\rho \quad &\text{if } y = \text{h}(x) \\ &h\left(x\right)_{y_{\text{max}}} + h\left(x\right)_{\text{h}(x)} + \rho \quad &\text{if } y = y_{\text{max}} \\ \end{aligned}\right.\)滿足約束\(\sum_{y\in \mathcal{Y}}h_{\rho}(y\mid x)=0\)，其中\(y_{\max} = \underset{y\in \mathcal{Y}}{\text{arg max}}\space p(y\mid x)\)，則對任意\(h\in \mathcal{H}\)有：

\[\begin{aligned} &\sum_{y\in \mathcal{Y}}\left(1 - p(y\mid x)\right)\max\left\{0, 1 + \frac{h(x)_y}{\rho}\right\} - n\left(1 - \max_{y\in \mathcal{Y}}p\left(y\mid x\right)\right) \\ &\geqslant \sum_{y\in \mathcal{Y}}\left(1 - p(y\mid x)\right)\min\left\{n, \max\left\{0, 1 + \frac{h(x)_y}{\rho}\right\}\right\} - n\left(1 - \max_{y\in \mathcal{Y}}p\left(y\mid x\right)\right) \\ &\geqslant \sum_{y\in \mathcal{Y}}\left(1 - p(y\mid x)\right)\min\left\{n, \max\left\{0, 1 + \frac{h(x)_y}{\rho}\right\}\right\} \\ &\quad - \sum_{y\in \mathcal{Y}}\left(1 - p(y\mid x)\right)\min\left\{n, \max\left\{0, 1 + \frac{h_{\rho}(x)_y}{\rho}\right\}\right\} \\ &= \left(p(y_{\text{max}}\mid x) - p(\text{h}(x)\mid x)\right)\min\left\{n, 1 + \frac{h(x)_{\text{h}(x)}}{\rho}\right\} \\ &\geqslant \max_{y\in \mathcal{Y}}p\left(y\mid x\right) - p\left(\text{h}\left(x\right)\mid x\right) \end{aligned} \]

和之前\(\mathcal{l}_{mae}\)、\(\mathcal{l}_{\rho}\)的證明類似，這個結論我們會在后面的證明中多次用到。

于是和之前\(\mathcal{l}_{mae}\)、\(\mathcal{l}_{\rho}\)類似，我們有

于是

為了構建\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x)\)和\(\Gamma \left(\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x)\right)\)的不等式關系，接下來我們將會采用\(\mathcal{l}_{\text{mae}}\)、\(\mathcal{l}_{\rho}\)的證明中類似的做法，針對\(\max_{y\in \mathcal{Y}} p(y\mid x)\)與\(1 - c\)的大小比較情況與\(r(x)\)的符號情況來對\(\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x)\)進行分類討論：

1. \(\max_{y\in \mathcal{Y}} p(y\mid x) > (1 - c)\)，\(r(x) > 0\)：
   此時

   \[\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x) \geqslant \max_{y\in \mathcal{Y}}p(y\mid x) - p(\text{h}(x)\mid x) = \Delta C_{\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x)^2 \]

   取\(\Gamma_1 (z) = z\)，于是\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x) \leqslant \Gamma (\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x))\)得證。

2. \(\max_{y\in \mathcal{Y}} p(y\mid x) \leqslant (1 - c)\)，\(r(x) > 0\)：
   此時

   \[\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x) \geqslant \frac{1}{4n}\left(1 - c - p\left(\text{h}\left(x\right)\mid x\right)\right)^2 = \frac{\Delta C_{\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x)^2}{4n} \]

   取\(\Gamma_2 (z) = 2\sqrt{nz}\)，于是\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x) \leqslant \Gamma (\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x))\)得證。

3. \(\max_{y\in \mathcal{Y}} p(y\mid x) \leqslant (1 - c)\)，\(r(x) \leqslant 0\)：
   由于此時\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x) = 0\)，因此\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x) \leqslant \Gamma (\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x))\)對任意\(\Gamma \geqslant 0\)成立。

4. \(\max_{y\in \mathcal{Y}} p(y\mid x) > (1 - c)\)，\(r(x) \leqslant 0\)：
   此時

   \[\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x) \geqslant n\left(\frac{\max_{y\in \mathcal{Y}}p(y\mid x) - 1 + c}{2}\right)^2 = \frac{n\Delta C_{\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x)^2}{4} \]

   取\(\Gamma_3 (z) = 2\sqrt{z/n}\)，于是\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x) \leqslant \Gamma (\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x))\)得證。

綜上所述，若取\(\Gamma(z) = \max\{\Gamma_1(z), \Gamma_2(z), \Gamma_3(z)\} = \max\{2\sqrt{nz}, z\}\)，則恒有\(\Delta C_{L_\text{abst}, \mathcal{H}, \mathcal{R}}(h, r, x) \leqslant \Gamma (\Delta C_{L, \mathcal{H}, \mathcal{R}}(h, r, x))\)。于是\(\mathcal{l} = \mathcal{l}_{\rho-\text{hinge}}\)，\(\psi(z) = nz\)時單階段代理損失的\((\mathcal{H}, \mathcal{R})\)-一致性界得證。

參考

• [1] Mao A, Mohri M, Zhong Y. Predictor-rejector multi-class abstention: Theoretical analysis and algorithms[C]//International Conference on Algorithmic Learning Theory. PMLR, 2024: 822-867.
• [2] Ni C, Charoenphakdee N, Honda J, et al. On the calibration of multiclass classification with rejection[J]. Advances in Neural Information Processing Systems, 2019, 32.