塊狀數(shù)組的基本用法:把數(shù)組變成靈活的積木
生活中處處可見(jiàn)分塊思想的影子。走進(jìn)圖書(shū)館,書(shū)籍按照學(xué)科分類(lèi),讀者只需先定位大類(lèi)別,再在小范圍內(nèi)查找,就能快速找到目標(biāo)書(shū)籍;小區(qū)的快遞柜更是將大量包裹按照格口大小和編號(hào)分塊存放,快遞員按區(qū)域投放,收件人按編號(hào)取件,極大提升了物流效率。這種 “先整體劃分,再局部處理” 的思路,在算法世界中演變成了一種高效的數(shù)據(jù)結(jié)構(gòu) —— 塊狀數(shù)組。
在處理數(shù)組問(wèn)題時(shí),我們也可以使用分塊思想構(gòu)建塊狀數(shù)組。
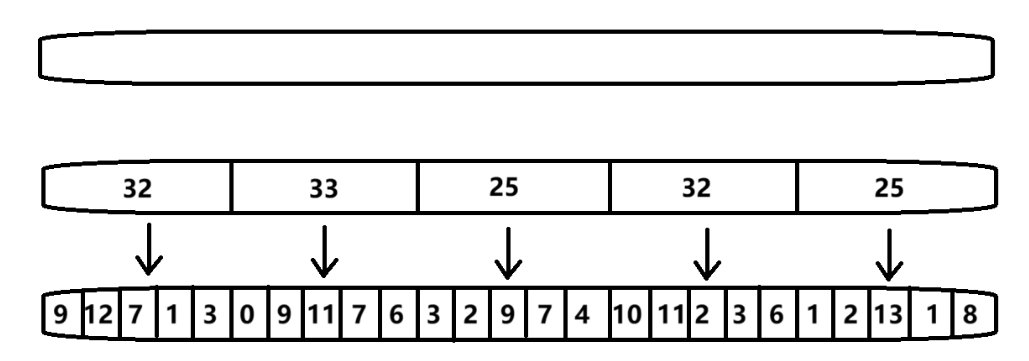
將一個(gè)長(zhǎng)度為 \(n\) 的線(xiàn)性數(shù)組,按照一定規(guī)則分割成若干個(gè)連續(xù)的子數(shù)組(我們稱(chēng)之為 “塊”)。每個(gè)塊的大小通常設(shè)定在 \(\sqrt n\) 左右(取得塊大小和塊數(shù)量的平衡)。例如,對(duì)于長(zhǎng)度為 100 的數(shù)組,我們可以將其劃分為 10 個(gè)塊,每個(gè)塊包含 10 個(gè)元素;若數(shù)組長(zhǎng)度為 1000,則可分成 32 個(gè)塊(因?yàn)?√1000≈31.62),前 31 個(gè)塊各含 32 個(gè)元素,最后一個(gè)不完整塊包含剩余的 28 個(gè)元素。
vector<vector<int>> init_block_array(const vector<int>& arr) {
int n = arr.size();
if (n == 0) return {};
int block_size = ceil(sqrt(n)); // 向上取盡可能避免最后的大小極小的塊
int block_num = (n + block_size - 1) / block_size; // 計(jì)算總塊數(shù)
vector<vector<int>> blocks(block_num);
for (int i = 0; i < n; ++i) {
int block_idx = i / block_size; // 計(jì)算元素所屬塊編號(hào)
blocks[block_idx].push_back(arr[i]);
}
return blocks;
}
這樣一來(lái),原本線(xiàn)性排列的數(shù)組就被 “拆解” 成了若干個(gè)可獨(dú)立操作的 “積木塊”,為后續(xù)的區(qū)間操作奠定了基礎(chǔ)。
從內(nèi)存結(jié)構(gòu)上看,塊狀數(shù)組相當(dāng)于在原數(shù)組的基礎(chǔ)上增加了一層 “塊級(jí)索引”,這層索引就像圖書(shū)館的區(qū)域?qū)б晥D,讓我們能批量快速的編輯這些 “區(qū)域”。
塊狀數(shù)組的基本用法
塊狀數(shù)組的真正價(jià)值,在于它能像搭積木一樣靈活處理數(shù)組的區(qū)間操作。當(dāng)我們需要對(duì)一個(gè)連續(xù)區(qū)間進(jìn)行更新或查詢(xún)時(shí),不必逐個(gè)遍歷元素,而是可以利用 “塊” 的特性批量處理,大幅提升效率。僅僅在區(qū)間邊界處理單個(gè)數(shù)。
區(qū)間加 - 區(qū)間和問(wèn)題
這個(gè)經(jīng)典問(wèn)題可以用各種數(shù)據(jù)結(jié)構(gòu)話(huà)花式解決,分塊也可以。核心是為每個(gè)塊維護(hù)兩個(gè)關(guān)鍵信息:加法標(biāo)記和塊內(nèi)元素和。加法標(biāo)記記錄了需要對(duì)整個(gè)塊執(zhí)行的累加操作,類(lèi)似于給一整箱積木貼上 “每個(gè)積木加 3” 的標(biāo)簽;塊內(nèi)元素和則預(yù)先存儲(chǔ)了當(dāng)前塊所有元素的總和,避免每次查詢(xún)時(shí)重新計(jì)算。
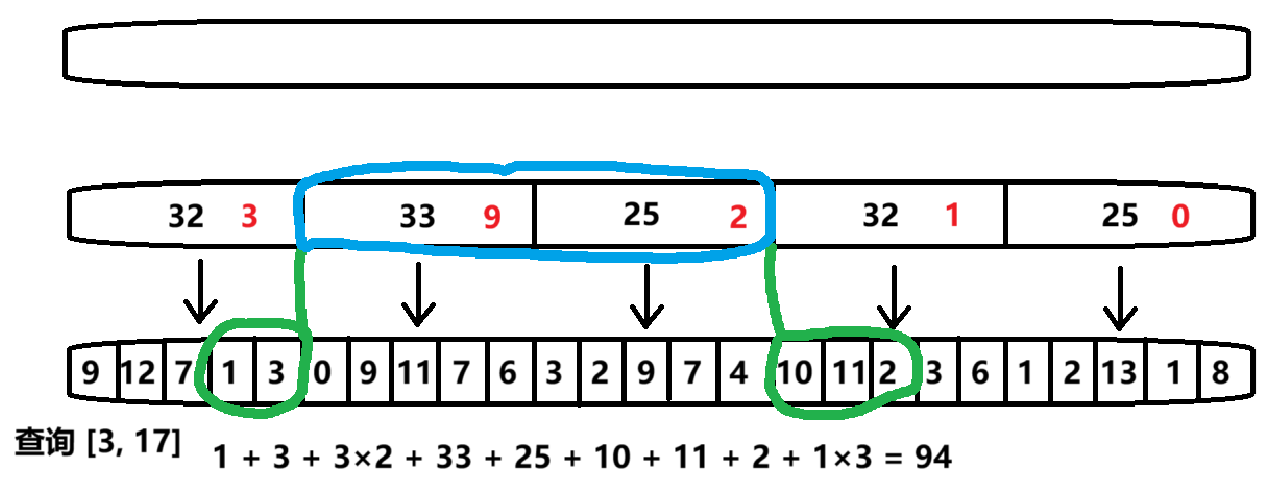
以區(qū)間加操作為例子,我們將目標(biāo)區(qū)間分為三部分處理:
-
左側(cè)邊緣塊:區(qū)間起始位置所在的不完整塊,需要逐個(gè)遍歷元素執(zhí)行加法操作,并同步更新塊內(nèi)元素和。
-
中間完整塊:完全包含在目標(biāo)區(qū)間內(nèi)的塊,直接更新其加法標(biāo)記(如將標(biāo)記值 + 5),同時(shí)通過(guò) “塊大小 × 增量” 快速更新塊內(nèi)元素和,而不處理中間塊之中的元素。
-
右側(cè)邊緣塊:區(qū)間結(jié)束位置所在的不完整塊,處理方式同左側(cè)邊緣塊。
最佳塊大小的數(shù)學(xué)證明
這種處理方式的巧妙之處在于,完整塊的操作只需 \(O (1)\) 時(shí)間,而邊緣塊最多涉及兩個(gè)塊。
為什么塊大小選擇 \(\sqrt n\) 能達(dá)到最優(yōu)效率?假設(shè)塊大小為 \(s\),總塊數(shù)則為 \(n/s\)。對(duì)于任意區(qū)間操作,最多需要處理 2 個(gè)邊緣塊(共 \(O (s)\) 時(shí)間)和 \(O (n/s)\) 個(gè)完整塊(共 \(O (n/s)\) 時(shí)間)。總時(shí)間復(fù)雜度為 \(O (s + n/s)\),根據(jù)均值不等式, \(s = \sqrt n\) 時(shí),復(fù)雜度達(dá)到最優(yōu)的 \(O (\sqrt n)\)。
一般來(lái)講,取根號(hào)都是最優(yōu)的,達(dá)到了塊大小和塊數(shù)量的平衡。某些特定情況可能需要取其他的塊大小。
struct BlockArray {
vector<int> arr; // 原始數(shù)組
vector<long long> sum; // 每個(gè)塊的元素和
vector<int> add; // 每個(gè)塊的加法標(biāo)記
int block_size; // 塊大小
int block_num; // 塊數(shù)量
BlockArray(const vector<int>& data) {
// ...
// 初始化塊內(nèi)和
for (int i = 0; i < n; ++i) {
int bid = i / block_size;
sum[bid] += arr[i];
}
}
// 區(qū)間[l, r]加val
void range_add(int l, int r, int val) {
int left_bid = l / block_size;
int right_bid = r / block_size;
// 只有一塊
if (left_bid == right_bid) {
for (int i = l; i <= r; ++i) {
arr[i] += val;
}
sum[left_bid] += val * (r - l + 1); // 記得更新總和
return;
}
// 左側(cè)完整部分
for (int i = l; i < (left_bid + 1) * block_size; ++i) {
arr[i] += val;
}
sum[left_bid] += val * (block_size - l % block_size);
// 中間完整塊
for (int bid = left_bid + 1; bid < right_bid; ++bid) {
add[bid] += val;
sum[bid] += val * block_size;
}
// 右側(cè)邊緣塊
for (int i = right_bid * block_size; i <= r; ++i) {
arr[i] += val;
}
sum[right_bid] += val * (r % block_size + 1);
}
// 查詢(xún)區(qū)間[l, r]的和
long long range_sum(int l, int r) {
int left_bid = l / block_size;
int right_bid = r / block_size;
long long res = 0;
if (left_bid == right_bid) {
for (int i = l; i <= r; ++i) {
res += arr[i] + add[left_bid];
}
return res;
}
// 左側(cè)邊緣
for (int i = l; i < (left_bid + 1) * block_size; ++i) {
res += arr[i] + add[left_bid];
}
// 中間完整塊
for (int bid = left_bid + 1; bid < right_bid; ++bid) {
res += sum[bid];
}
// 右側(cè)邊緣
for (int i = right_bid * block_size; i <= r; ++i) {
res += arr[i] + add[right_bid];
}
return res;
}
};
區(qū)間加乘 - 區(qū)間和問(wèn)題
當(dāng)問(wèn)題升級(jí)為同時(shí)包含加法和乘法的區(qū)間操作時(shí),我們需要再引入乘法標(biāo)記 mul(初始值為 1),并嚴(yán)格處理兩種標(biāo)記的優(yōu)先級(jí)。由于乘法對(duì)加法有分配律(a*val1 + val2),正確的處理順序應(yīng)為先乘后加。
-
當(dāng)對(duì)塊執(zhí)行乘法操作(乘 m)時(shí):
- mul = mul * m
- add = add * m
- sum = sum * m
-
當(dāng)對(duì)塊執(zhí)行加法操作(加 a)時(shí):
- add = add + a
- sum = sum + a * 塊大小
在處理邊緣塊的單個(gè)元素時(shí),需要先應(yīng)用乘法標(biāo)記,再應(yīng)用加法標(biāo)記:arr[i] = arr[i] * mul[bid] + add[bid]。
仍然是根號(hào)復(fù)雜度,代碼就不再演示了。
| 數(shù)據(jù)結(jié)構(gòu) | 支持操作 | 構(gòu)建復(fù)雜度 | 單次查詢(xún) | 單次更新 | 實(shí)現(xiàn)難度 | 適用場(chǎng)景 & 優(yōu)缺點(diǎn) |
|---|---|---|---|---|---|---|
| 塊狀數(shù)組(√分塊) | 區(qū)間求和、區(qū)間加、區(qū)間眾數(shù)等 | \(O(n)\) 或 \(O(n\sqrt n)\)(眾數(shù)) | \(O(\sqrt n)\) 或 \(O(\sqrt n\log n)\)(眾數(shù)) | \(O(1)\)–\(O(\sqrt n)\)(區(qū)間加需延遲) | ★★☆☆☆ | + 實(shí)現(xiàn)簡(jiǎn)單、常數(shù)低 – 查詢(xún)/更新均攤 \(O(\sqrt n)\),規(guī)模更大時(shí)不夠快 |
| 線(xiàn)段樹(shù) | 區(qū)間求和/最值/GCD/加標(biāo)記等 | \(O(n)\) | \(O(\log n)\) | \(O(\log n)\) | ★★★☆☆ | + 支持幾乎所有區(qū)間操作、可加懶標(biāo)記 – 實(shí)現(xiàn)稍復(fù)雜,常數(shù)較大 |
| 樹(shù)狀數(shù)組(BIT) | 前綴和、區(qū)間加 & 單點(diǎn)查、區(qū)間和 | \(O(n)\) | \(O(\log n)\) | \(O(\log n)\) | ★☆☆☆☆ | + 結(jié)構(gòu)緊湊、易實(shí)現(xiàn) – 只支持前綴/區(qū)間和,難以做區(qū)間最值、區(qū)間眾數(shù)等 |


 浙公網(wǎng)安備 33010602011771號(hào)
浙公網(wǎng)安備 33010602011771號(hào)