位運算處理N皇后
n皇后問題位運算版
n皇后問題是啥我就不說了吧,學編程的肯定都見過。下面的十多行代碼是n皇后問題的一個高效位運算程序,
看到過的人都夸它牛。初始時,upperlim:=(1 shl n)-1。主程序調用test(0,0,0)后sum的值就是n皇后總的解數。
procedure test(row,ld,rd:longint);
var
pos,p:longint;
begin
{ 1} if row<>upperlim then
{ 2} begin
{ 3} pos:=upperlim and not (row or ld or rd);
{ 4} while pos<>0 do
{ 5} begin
{ 6} p:=pos and -pos;
{ 7} pos:=pos-p;
{ 8} test(row+p,(ld+p)shl 1,(rd+p)shr 1);
{ 9} end;
{10} end
{11} else inc(sum);
end;
乍一看似乎完全摸不著頭腦,實際上整個程序是非常容易理解的。這里還是建議大家自己單步運行一探究竟,實在沒研究出來再看下面的解說。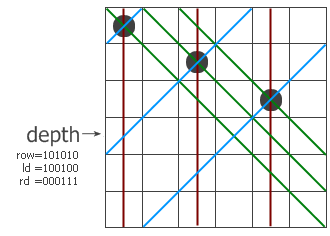
和普通算法一樣,這是一個遞歸過程,程序一行一行地尋找可以放皇后的地方。過程帶三個參數,row、ld和rd,
分別表示在縱列和兩個對角線方向的限制條件下這一行的哪些地方不能放。我們以6x6的棋盤為例,看看程序是怎么工作的。
假設現在已經遞歸到第四層,前三層放的子已經標在左圖上了。紅色、藍色和綠色的線分別表示三個方向上有沖突的位置,
位于該行上的沖突位置就用row、ld和rd中的1來表示。把它們三個并起來,得到該行所有的禁位,
取反后就得到所有可以放的位置(用pos來表示)。
前面說過-a相當于not a + 1,這里的代碼第6行就相當于pos and (not pos + 1),其結果是取出最右邊的那個1。
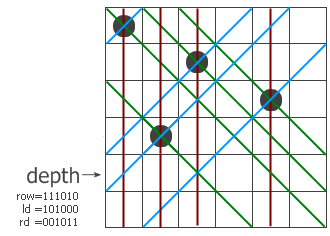
這樣,p就表示該行的某個可以放子的位置,把它從pos中移除并遞歸調用test過程。注意遞歸調用時三個參數的變化,
每個參數都加上了一個禁位,但兩個對角線方向的禁位對下一行的影響需要平移一位。最后,
如果遞歸到某個時候發現row=111111了,說明六個皇后全放進去了,此時程序從第1行跳到第11行,找到的解的個數加一。
根據上面的理論,可以解決下面的這道題目。
Sample Input
6
Sample Output
2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4
#include<iostream>
using namespace std;
#define Max 14
int Row[Max], n, numofsolve;
void SolveWithBit(int p, int row, int lb, int rb)
{
if(p>n) //找到了解
{
numofsolve++;
if(numofsolve <=3) //判斷解的個數
{
for(int i=1; i<n; i++)
cout<<Row[i]<<" ";
cout<<Row[n]<<endl;
}
}
for(int i=1; i<=n; i++)
{
int t = (1<<(i-1)); //用t來試探可用位置
if((t & (row | lb | rb))==0) //(row | lb | rb)表示本行中所有禁用的位置,t就是表示本行中所有的可用位
{
Row[p] = i; //i位可用
SolveWithBit(p+1, row|t, (lb|t)<<1, (rb|t)>>1);
}
}
}
int main()
{
cin>>n;
int re;
for(int i=1; i<=n; i++)
{
Row[1] = i; //初始化第一行,有n個狀態
SolveWithBit(2, 1<<(i-1), 1<<i, 1<<(i-2)); //從第二行開始搜索
}
cout<<numofsolve<<endl;
}
posted on 2011-10-17 08:45 More study needed. 閱讀(807) 評論(0) 收藏 舉報


 浙公網安備 33010602011771號
浙公網安備 33010602011771號