``# 二進制的數與位
在計算機的代碼世界中，是以二進制的位的基礎來組成數，至此我還是混淆，二級制的1000（十進制的8）中的1是第4個數字還是第3位數字

學過二進制的都知道，二級制只有0和1，通過2為底數，乘上冪計算得到的，其中冪的大小取決于在第幾位,比如1000的1的冪的大小為3，則這個二級制位置的數值就為 \(2^3=8\)^[1]

由2進制的計算方法，可以推理出n進制的計數方法，也就是位值計算法^[2],這中計數法區別于我們的日常計數法。

日常的思維和計數法

為什么我們會把“514￥”念作“五百一十四 塊錢”，而不是“五一四 塊錢”呢？其實，念出“五百一十四”的時候，我們就已經進行了一遍以數值乘 10為底數冪為1-十、2-百的計算 然后加起來的過程

在這里個位數是第 1個數字，計算的過程是 四*1， 依次類推，整個計算的過程就是

五*100+一*十+四*1

所以我們從小開始思維一直就是以十進制來記憶，第 1個數字是個，第 2個數字是十，第 3個數字是百。

其實在學n進制之前，我們小學數學的十進制計數方法是按順序記憶的^[3]，并沒有指數和位值的說法。

n進制的位權

學了n進制之后，我們知道了， 底數的冪其實是 位權（weight），即“每位的權重”。

按照日常的思維，對于十進制來說，第\(i\)位的位權其實就是 \(10^{i-1}\)，對于二進制來說，第\(i\)位的位權其實就是\(2^{i-1}\)，一般的，對于n進制來說，第\(i\)位的位權其實就是\(n^{i-1}\)

還是五百一十四，四是第1位數字，位權其實就是\(10^0\)

但是按照計算機的思維和n進制的位權來定義，并不是這樣的

打開微軟自帶的計算器軟件，可以看到二進制的位置的標號

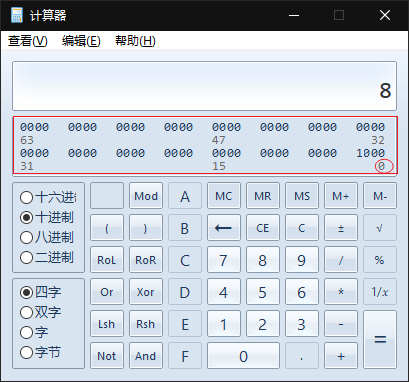
按照計算機的思維，第1個數字的標號是0，位權的公式正確的來說應該是\(10^{i}\)，對于二進制來說，第\(i\)位的位權其實就是\(2^{i}\)，一般的，對于n進制來說，第\(i\)位的位權其實就是\(n^{i}\)

總結

所以當五百一十四用計算機的思維，也就是十進制的說法的時候，其實四是第0位數字，而如果按照日常的思維來看四是第1個數字

按計算機思維，就是位值計數法，二級制的1000（十進制的8）中的1就是第3位數字，二級制而沒有日常思維的計數方法，只需要把思維轉變過來，就不會混淆了。

ps：我用了 個 來對應日常的思維，位來對應計算機思維。

數的產生和日常的十進制的歷史發展

日常的十進制的歷史發展和數的產生的歷史發展更適合放在一塊說

對于數字來說，主要的發展的歷史就是^[3:1]
原始人用石頭一一對應數目
古代的古埃及象形數字，巴比倫楔形數字，古羅馬數字，中國橫縱式算籌代表特定的數目
現代的阿拉伯數字，也就是我們說的自然數

這些數的產生和十進制相關，人類在算數時普遍采用“十進制”這一體系，其背后的原因可能與人類擁有十根手指這一解剖學特征緊密相關。亞里士多德曾指出，人類對十進制的普遍使用，正是基于這樣一個簡單的解剖學事實：我們每個人都有十根手指。只不過，這些十進制記數體系并不是按位的，沒有位值這個概念。^[4]:

所以無論在那個時期的數字的進位和十都是聯系緊密的，逢十進一的概念是日常習慣觀念了，但是我們用位值(指數/冪)表示更多是在學了二進制之后，起碼小學學數學的時候是沒有提到的。

換個說法區分日常的十進制和n進制的十進制就是看是不是用位值(指數/冪)來計算

二進制的起源和計算機的歷史發展

前面提到二進制是在計算機世界里面的，至于為什么會聯系起來，就可以看看這個計算機宇宙的八卦

ps： 我在此之前對這些名人是一點不感冒的，但是成為圈里人（程序員）之后，再去看這些名人和發展歷史就像八卦一樣津津有味。或許歷史就是當代人追八卦狂熱了，用專業的筆墨記下事實，是不是學習歷史的一個好方法就是成為圈里人。pps：記得我高一分文理科前，記憶力不好，但是歷史分數好像還是不錯的。

萊布尼茨：二進制的美妙的發源

在17世紀中葉，二進制由德國數學家戈特弗里德·威廉·萊布尼茨（德語：Gottfried Wilhelm Leibniz；1646年7月1日—1716年11月14日）在1703年發表的論文《論只使用符號0和1的二進制算術，兼論其用途及它賦予伏羲所使用的古老圖形的意義》（Explication de l'arithmétique binaire, qui se sert des seuls caractères 0 et 1 avec des remarques sur son utilité et sur ce qu'elle donne le sens des anciennes figures chinoises de Fohy）
中系統地介紹了二進制數系統。^[5]:

二進制的美妙不同于前面的用 數來描述生活的數目，而是用數學的符號和計算，描述人類全部思想領域的符號系統

這種思想是超前的，按照現在來看，不就是我們現在使用的計算機，用計算機語言表達出人類的思想領域的內容

當然萊布尼茨的二級制的啟發也是有根據的，但是具體根據沒有確認，不過這些依據的大體的思想表達都是相似的：

• 亞里士多德把概念分成固定的“范疇”^[6]:
• 中國的八卦和《易經》中的二元思想

關于萊布尼茨的二級制的啟發是不是受中國《易經》的啟發，就像是網絡熱點惹人研究，網上可以看到很多人討論^[7],也有專業的去研究過，我也八卦了下。從參考文章來看確實有兩個觀點：

郭書春在《古代世界數學泰斗劉徽》一書461頁中稱：“中國有所謂《周易》創造了二進制的說法，至于萊布尼茲受《周易》八卦的影響創造二進制并用于計算機的神話，更是廣為流傳。事實是，萊布尼茲先發明了二進制，后來才看到傳教士帶回的宋代學者重新編排的《周易》八卦，并發現八卦可以用他的二進制來解釋。”以此為由，認為并不是萊布尼茨看到陰陽八卦才發明二進制。梁宗巨著《數學歷史典故》（1995年出版）一書14～18頁對這一歷史公案亦有此說。

胡陽、李長鐸在《萊布尼茨發明二進制前沒有見過先天圖嗎——對歐洲現存17世紀中西交流文獻的考證》通過對歐洲現存17世紀中西交流文獻的研究考證，否定了萊布尼茨在發明二進制以后才見到先天圖的說法。先天圖在萊布尼茨發明二進制之前，已被斯比塞爾稱之為二進制。

其實按照參考文章的作者的觀點更加好：
除了萊布尼茨個人的獨創性的偉大貢獻外，近代意義上的二進制實際上是“中西合璧”的產物^[8]。

雖然萊布尼茲的論文提出了二進制可以作為新的計數方法，并可以完成基本的運算，但是卻沒有完成二進制的核心運算方法，也就是還沒有找到用數學的符號描述人類思想的具體實現路徑，直到布爾的研究發表。

布爾：從邏輯到代數

1854年，英國數學家喬治·布爾（英語：George Boole，1815年11月2日—1864年12月8日）發表了一篇里程碑式的論文，其中詳細介紹了一種代數化的邏輯系統，后人稱之為布爾代數。并在其代數中系統地應用了“真與假”的思想（即0與1）。

這里提到的代數就是也就是我們熟知的布爾運算（如與、或、非等），而邏輯就是人類概念的真假。

單從布爾運算來說，布爾的邏輯代數似乎是用一種特例的方式，描述人類思想領域的一角的真假邏輯而已。但二進制至此有了代數方法，數理邏輯從此就開始不斷發展。

香農：數電之父

1937年，克勞德·香農（英語：Claude Elwood Shannon，1916年4月30日—2001年2月24日）在麻省理工大學完成了其電氣工程碩士學位論文，用繼電器和開關實現了布爾代數和二進制算術運算。論文題為《繼電器與開關電路的符號分析》（A Symbolic Analysis of Relay and Switching Circuits），其中香農的理論奠定了數字電路的理論基礎，香農憑這篇論文于1940年被授予美國阿爾弗雷德·諾貝爾協會美國工程師獎。哈佛大學的哈沃德·加德納稱，香農的碩士論文“可能是本世紀最重要、最著名的碩士學位論文”。^[5:1]。

學電的都知道有三大本書是基礎：電路，模電，數電，現在來看最后一個數電其實就是源于香農的研究，所以我自愿稱其為數電之父

ps 為啥我學的數電那么厚一本，都不愿意搞個小節介紹下香農等前人的歷史，不然我也不會提不起興趣學習

我認為，香農的研究重要性是將電子器件完成了bool運算，意味著可以通過用電來控制計算，也就是自動化計算，也是計算機的實現的第一步。之后的就是各個計算機之父的誕生了。

對于計算機的發展，各個計算機之父，還有第一臺計算機之爭等又是巨大的瓜，準備再起一篇文章記錄下，下面介紹的是和二進制相關的科學家。

喬治·斯蒂比茲: 數字計算機之父

1937年11月，任職于貝爾實驗室的喬治·斯蒂比茲發明了用繼電器表示二進制的設備。它是第一臺二進制電子計算機^[5:2]。這個主要貢獻是硬件計算機的研發。

馮·諾依曼:現代計算機之父

為了改進使用十進制的第一臺通用計算機ENIAC，馮·諾依曼再1945年6月發表了一份關于EDVAC長達101頁的報告，報告提出的馮·諾伊曼結構一直延續至今^[9]。報告提出以二進制替代十進制，因電子元件的“雙穩態”（開/關）天然匹配二進制邏輯。其“存儲程序”設計（指令與數據共存于存儲器）奠定現代計算機五大結構基礎^[10]。

一些思考

其實這個二進制的思考也是源于存儲器的大小和二進制數字的大小，每次看到1024，4k，1g這樣的數字，還是感到陌生并在cmd輸入calc，看看不同進制下的數字大小。后續有空完善下計算機歷史，和存儲大小的探索筆記。

參考和引用