https://www.luogu.com.cn/problem/CF1214H

小思維+corner

考慮怎么染色，先找到直徑，直徑肯定是輪換染色，然后找到中心，
拉出來相同 dep 染一個顏色就行，這樣如果寄了肯定無解了。

https://www.luogu.com.cn/problem/CF1365G

二進制性質+分組優化

先考慮二進制分組，原理是任意兩個不同的數一定至少有一位二進制不同，但是這樣詢問次數多了。
考慮怎么優化，發現如果對于每個數，存在一定有一位這個數為 \(0\) 時，其他數字會為 \(1\)。
這樣的話每個二進制位就只用訪問一次了。
考慮直接構造把每個數換成二進制在 \(13\) 位下二進制位有 \(6\) 個位 \(1\) 的就好了因為 \(1\) 的次數 > \(0\) 的次數。

https://www.luogu.com.cn/problem/CF1379E

使用上下界構造并結合+分討

祖先關系還是比較好構造的，考慮兩種極限情況，一種長鏈每個節點多拉一個兒子，另一種是線段樹。
然后直接組合就可以了，因為第二種沒有個數限制，而第一種有一點。有一些corner，比如 \(n=9,k=2\) 無解。

https://www.luogu.com.cn/problem/CF1383D

矩陣填數+隊列輔助構造

好題，考慮怎么樣保留原始 \(S\) 中的數，那就是從大到小，每放一個就往自己原來是行還是列上移動一下。
考慮如何滿足先增后降的性質，考慮從填的這個數的左側和上側一次從從右到左，從下到上，
大到小填數，想象一下就知道了肯定滿足。

https://www.luogu.com.cn/problem/CF1491F

思考磁極性質 + 構造方案+觀察

考慮先找到一個有磁極的磁鐵，然后把這個磁鐵一一匹配。
這時我們發現找到第一個有磁極的磁鐵很有難度，因為要用到后面，所以我們找第二個有磁極的磁鐵。
我們每次查詢 \(1\to i\) 和 \(i+1\) 就可以知道 \(i+1\) 是不是第二個有磁極的磁鐵了。
然后我們可以和后面每個磁鐵一一匹配找到后面的磁鐵是不是有磁極的磁鐵。這兩步加起來用了 \(n-1\) 次。
發現 \([1,i]\) 只有一個有磁極的磁鐵，考慮二分，然后就做完了。

https://www.luogu.com.cn/problem/CF1491G

建圖+環融合處理+corner case

挺好一道題，先套路性自己的位置和自己的大小連邊，形成很多個簡單環。
考慮沒有翻轉怎么做，就是一個點交換一圈這樣就好了，如圖：

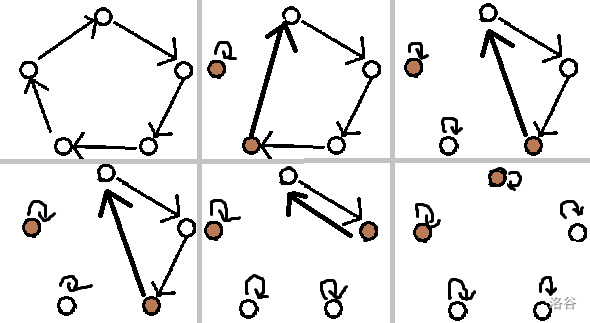
考慮加了翻轉，我們發現一個環要能直接刪干凈要有兩個背面的點，如圖：

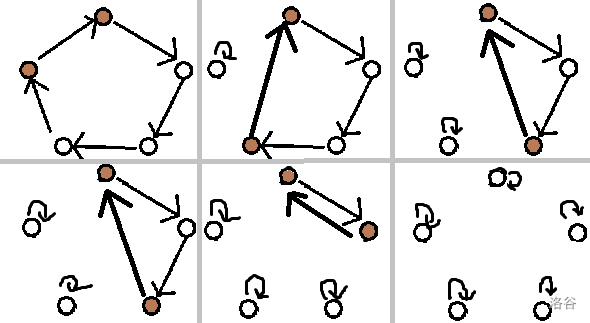
發現環內無法自己解決，考慮將兩個環內兩點交換，這樣就有兩個背面了，接下來是 corner。

如果只有一個環，最后一個環可以用 \(size+1\) 步做完。

考慮先交換兩個環上相鄰點，形成一個背面自環和一個帶一個背面點的環。
再把這個自環和一個環上正面點交換，這樣就有兩個背面的環了。

如果是 \(>1\) 個環且有奇數個環，考慮直接交換一個正面自環和環上一點，產生 兩個背面的環了。

分成兩種 corner 的原因是第二種環長可能為 \(2\)。

https://www.luogu.com.cn/problem/CF991F

大分討+時間復雜度分析

考慮任意一種情況都是 \(a\times b+c\) 其中 \(a,b,c\) 都是 \(X^Y\) 或者 \(X\) 或者無的形式，復雜度是對的直接分討。

https://www.luogu.com.cn/problem/CF1477D

圖上補圖構造+性質

先減少限制然后轉化為補圖，最后構造一種合法方案（菊花），我認為十分困難。