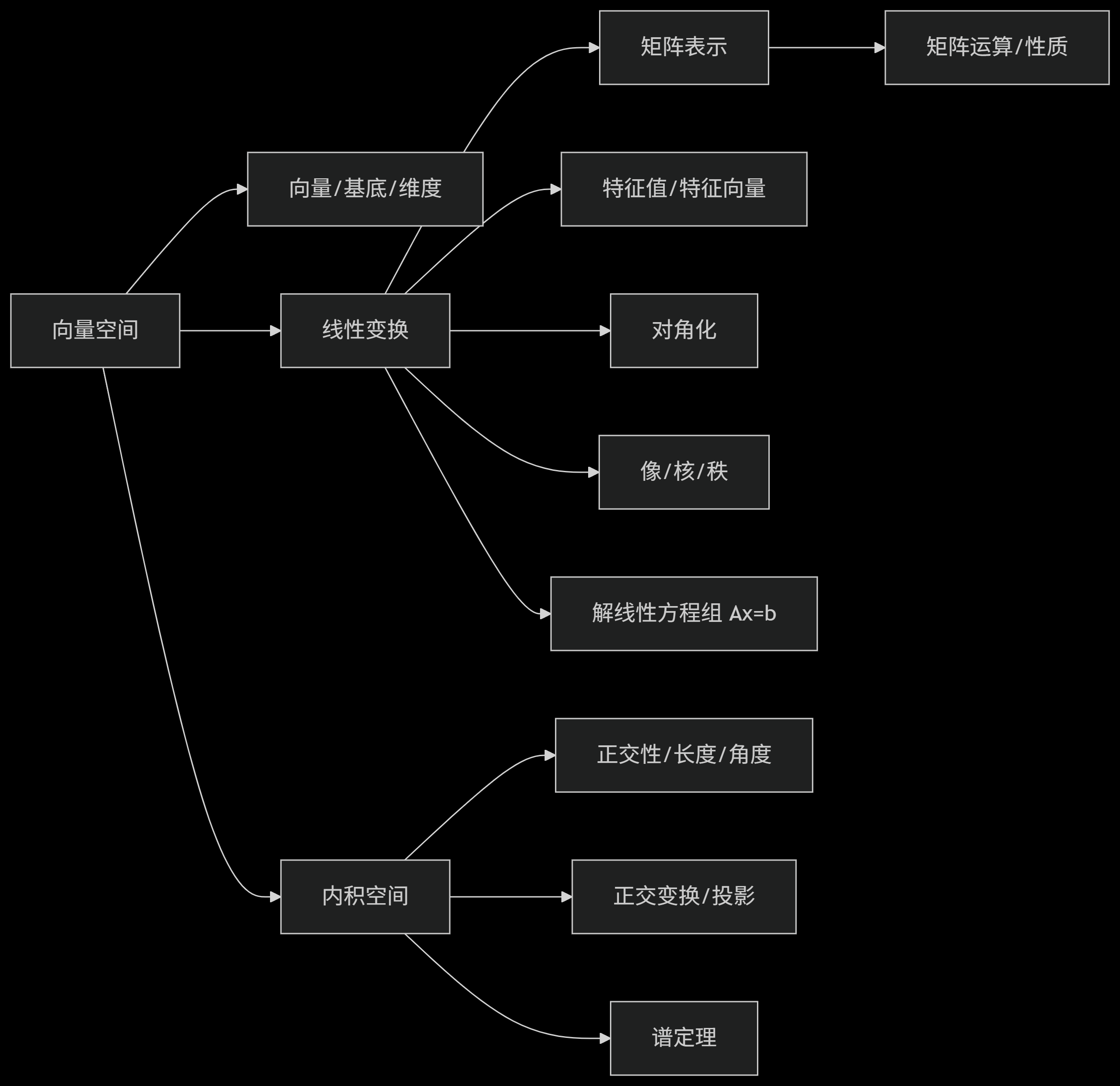
線性代數這門課程主要是理解空間上的變化，當然這個空間是被映射成數組形式了（空間也叫向量空間）。

• 向量空間是線性變換發生的“舞臺”。

• 線性變換是線性代數的核心概念和靈魂。 它提供了理解空間如何被操作、映射的根本視角。

  • 矩陣是描述和計算線性變換（以及在特定坐標系下描述向量）的核心工具。
  • 特征值/特征向量、對角化等是深入分析線性變換內在結構的關鍵工具。

• 求解線性方程組是線性變換理論的重要應用。

線性變化

線性變換 = 對空間的操作

想象一下，你有一張畫滿點的網格紙（代表整個空間）。線性變換就是對這張紙進行某種規則的“操作”，比如：

• 拉伸/壓縮： 把紙水平方向拉長2倍，垂直方向壓縮到一半。
• 旋轉： 把整張紙繞著原點（比如紙的中心點）旋轉30度。
• 剪切： 想象紙的上半部分向右推，下半部分保持不動，整張紙被“推斜”了。
• 鏡像： 把紙像照鏡子一樣翻折一下。

對空間的操作，是用一個數組（矩陣）去與另一個數組（向量）進行計算，得到一個新的數組（新向量）.

• 矩陣 是線性變換的“操作指令書，
• 向量 是空間中的一個點或方向，
• 矩陣×向量 就是施加變換的過程，
• 結果 是變換后的新點/方向。

這種計算不是簡單的“數組與數相乘”，而是遵循特定規則的 矩陣乘法，其核心思想是 重新組合基向量。

這也是計算機圖形學、物理仿真、機器學習中處理旋轉、縮放、投影等操作的基礎！