Why need Binary Tree?

有時候，我們希望數(shù)據(jù)按照特定順序排列。
比如：

• 想要按字母順序排列人名；
• 按價格順序排列產(chǎn)品；
• ...

樹也是節(jié)點結構

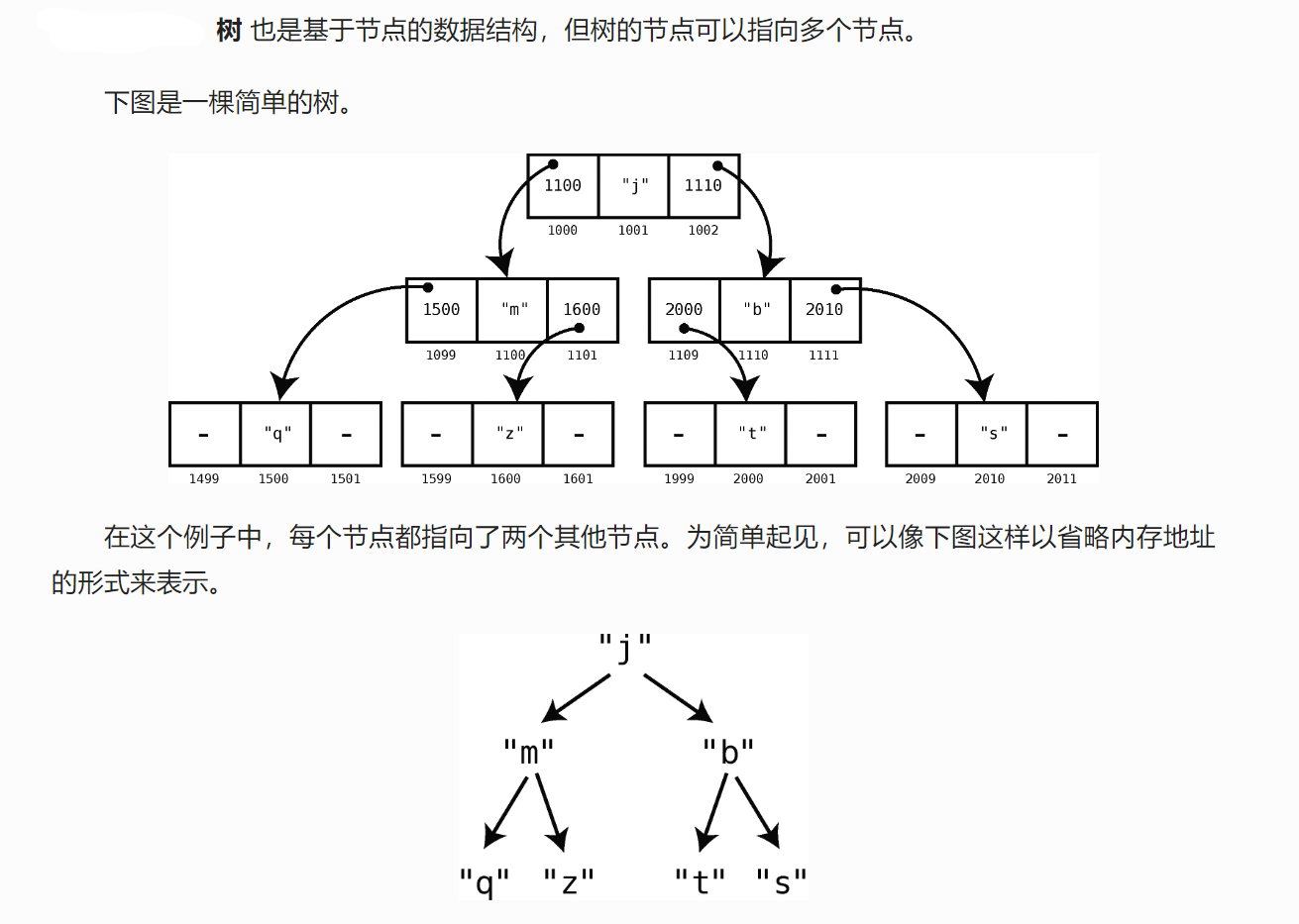
規(guī)定

• 二叉樹的每個節(jié)點的子節(jié)點數(shù)量都只能是0個 或1個、或2個；
• 每個節(jié)點最多有一個左子節(jié)點和右子節(jié)點；
• 一個節(jié)點的左子樹的值都 小于 節(jié)點本身，
• 一個節(jié)點的右子樹的值都 大于 節(jié)點本身；
• 這一規(guī)律適用于所有節(jié)點。

術語

• 層級
  

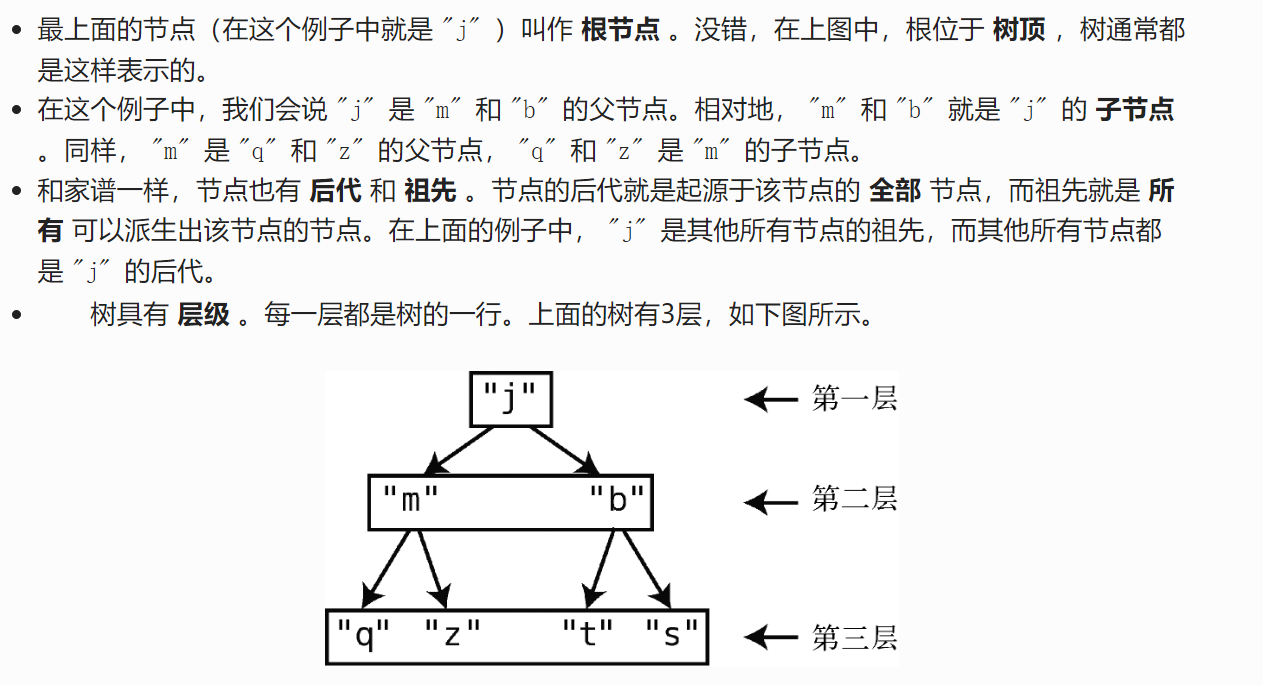
• 平衡
  

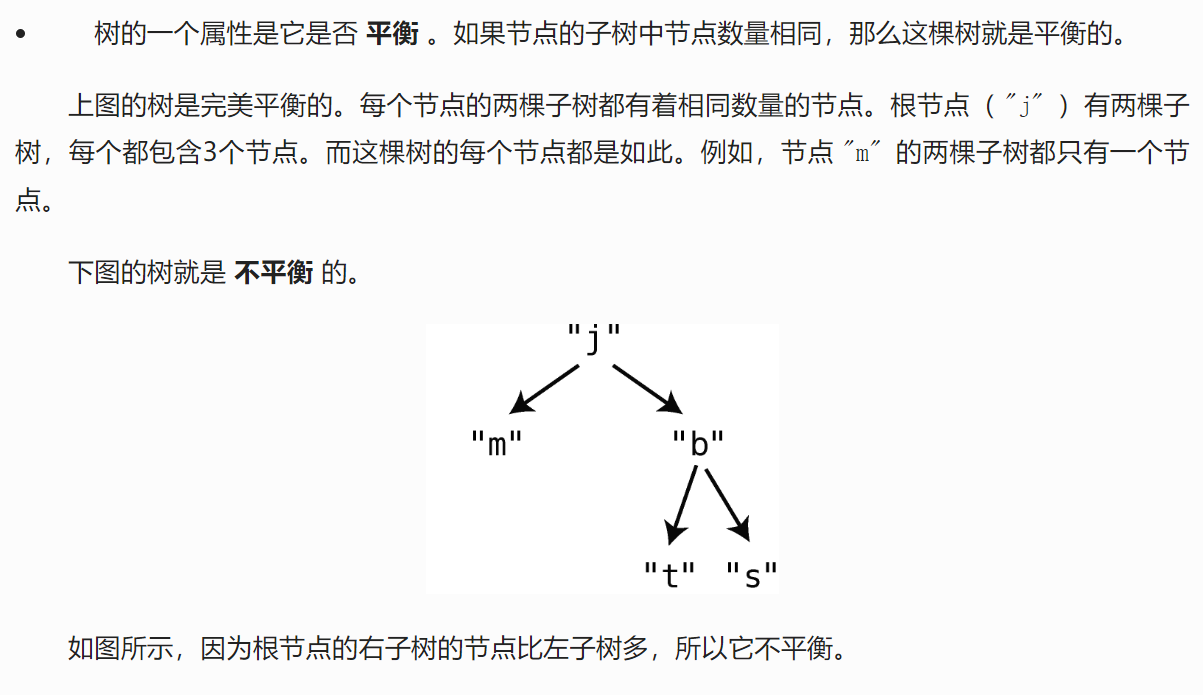
樹的創(chuàng)建

class TreeNode:
	def _init_(self, val, left=None, right=None):
		self.value = val
		self.leftChild = left
		self.rightChild = right

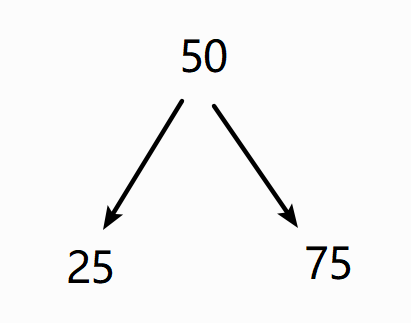
構建一棵簡單的樹:

node1 = TreeNode(25)
node2 = TreeNode(75)
root = TreeNode(50, node1, node2)

樹的查找

給你一顆二叉樹，

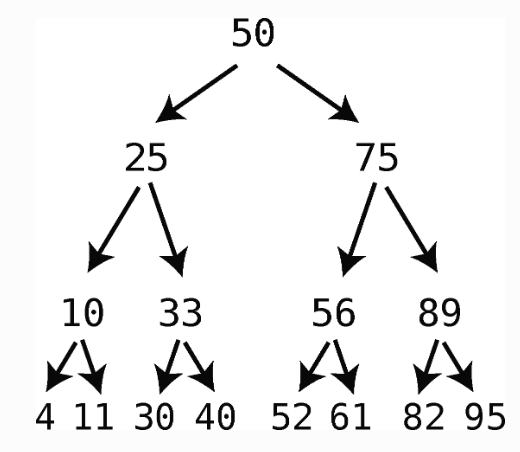
需要查找61，

查找步驟：

1. 算法開始時，根節(jié)點就是第一個“當前節(jié)點”；
   
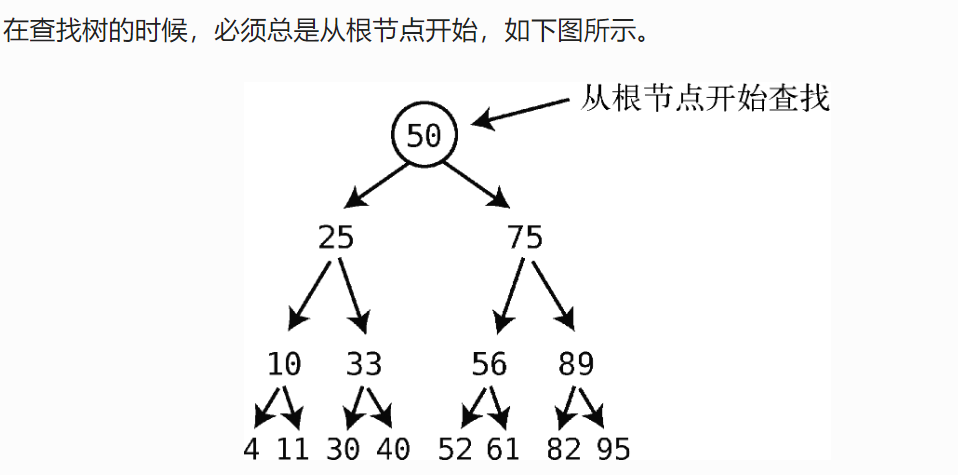
   檢查當前節(jié)點的值，如果時這個值，那就找到了。

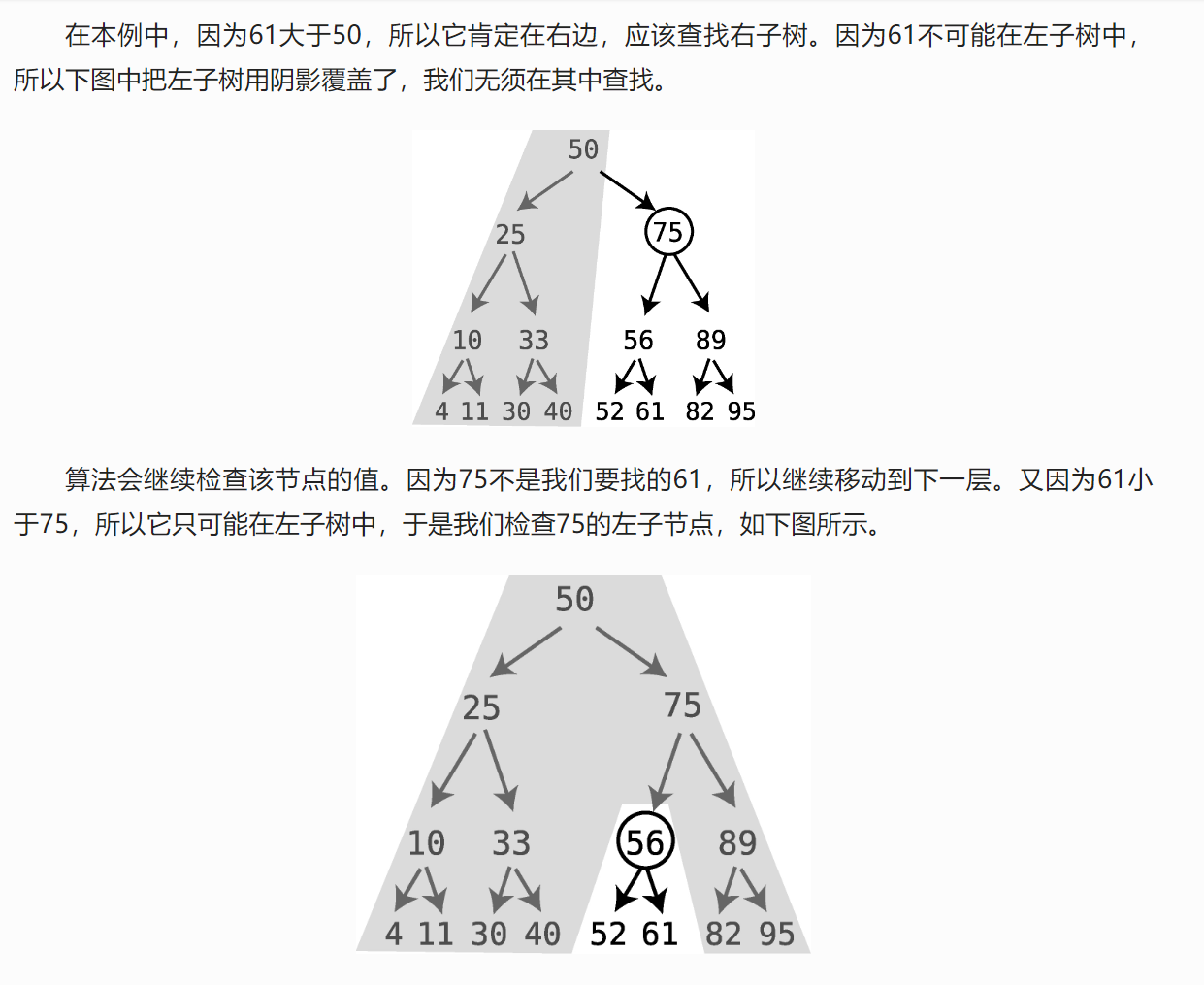
2. 如果要找到值小于當前節(jié)點值，那么就在其左子樹中繼續(xù)查找。

3. 如果要找的值大于當前節(jié)點的值，那么就在其右子樹中繼續(xù)查找。

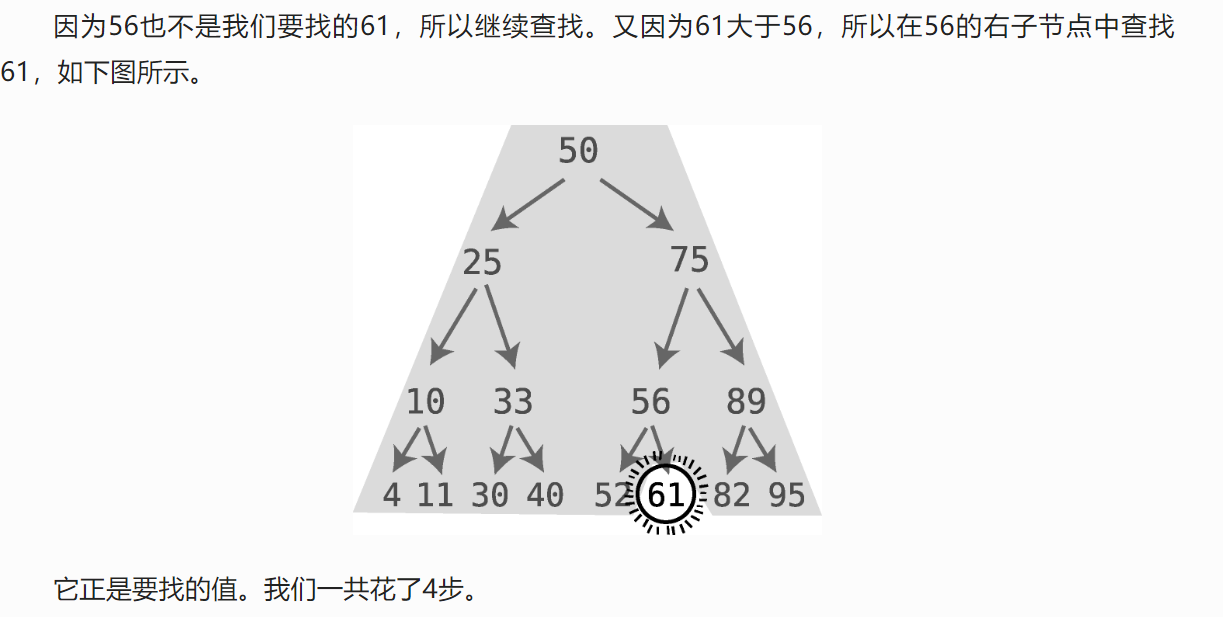
查找的效率

每一步排除了大約一半的剩余節(jié)點，因此，二叉查找樹的查找需要O（log N）時間。

樹的刪除

刪除是最復雜的操作。

需要區(qū)分這幾種情況：

• 沒有子節(jié)點；
• 有一個子節(jié)點；
• 有兩個子節(jié)點；
• 有多個子節(jié)點；

把所有步驟結合到一起，二又查找樹的刪除算法如下：

• 如果要刪除的節(jié)點沒有子節(jié)點，那么就直接刪除該節(jié)點。

• 如果要刪除的節(jié)點有一個子節(jié)點，那么就在刪除該節(jié)點的同時把子節(jié)點插到該節(jié)點的位置。

• 要刪除有兩個子節(jié)點的節(jié)點，需要把要刪除的節(jié)點替換為其 后繼 節(jié)點。后繼節(jié)點就是 大于被刪除節(jié)點的所有子節(jié)點中最小的那個。

  這個就是最復雜的情況，假設要圖這顆樹的56，
  
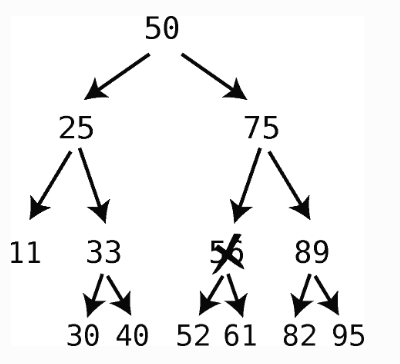
  需要把要刪除的節(jié)點替換為其 后繼 節(jié)點。后繼節(jié)點就是 大于被刪除節(jié)點的所有子節(jié)點中最小的那個。這個有點繞口！
  換一個說法：如果按升序排列被刪除節(jié)點及其后代，那么后繼節(jié)點就是被刪除節(jié)點的下一個數(shù)。
  

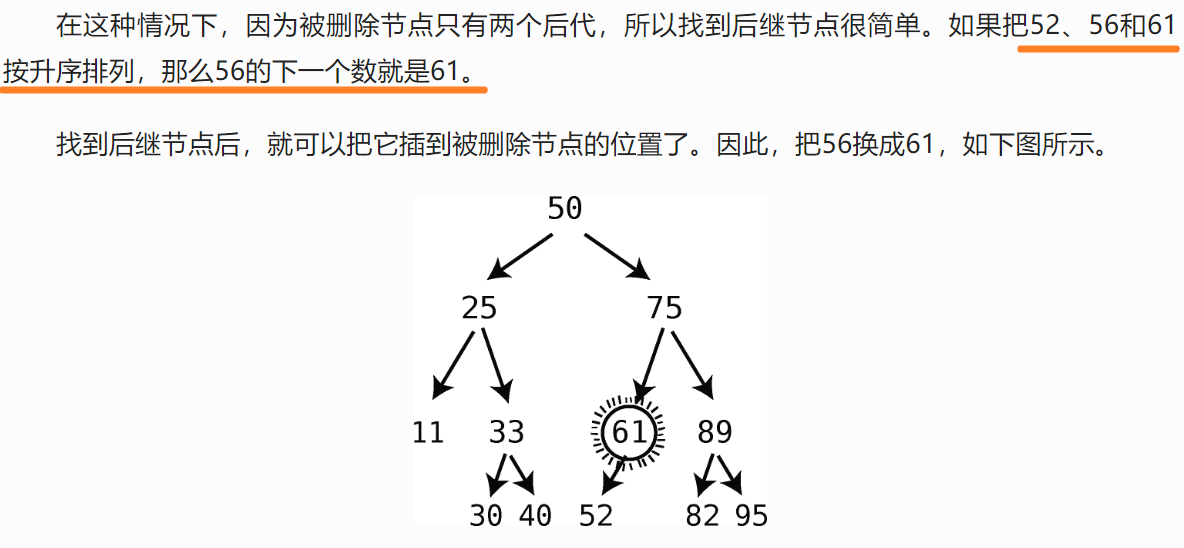
• 要刪除的節(jié)點在樹的頂端（也很復雜），尋找后繼節(jié)點的算法如下：

• 要尋找后繼節(jié)點，需要先移動到被刪除節(jié)點的右子節(jié)點，然后一直沿著左邊的鏈接移動到左子節(jié)點，直到找不到任何左子節(jié)點為止。最下面的這個值就是后繼節(jié)點。

• 如果后繼節(jié)點有一個右子節(jié)點，那么在把后繼節(jié)點放到被刪除節(jié)點的位置之后，把這個右子節(jié)點變成 后繼節(jié)點曾經(jīng)的父節(jié)點的左子節(jié)點。

二叉查找樹（BST）的刪除操作比較復雜，主要是因為在刪除節(jié)點后需要保持樹的性質，即每個節(jié)點的左子樹都要小于它，右子樹都要大于它。

適合場景

二叉查找樹的查找、插入、刪除效率都是(log N)，因此，它很適合那些需要存儲和操作有序數(shù)據(jù)的場合。

樹的遍歷

遍歷樹的方式有多種：

• 中序遍歷
• ...

使用遞歸的方式去遍歷樹...