遞歸和for循環（迭代法）很像，都是通過循環去完成一件事。

但采用Top-Down思維去設計的遞歸結構，又會比for多一些不同的能力。多什么能力？

遞歸的基礎

先復習一下遞歸，遞歸的定義：遞歸（英語：Recursion），又譯為遞回，在數學與計算機科學中，是指在函數的定義中使用函數自身的方法。

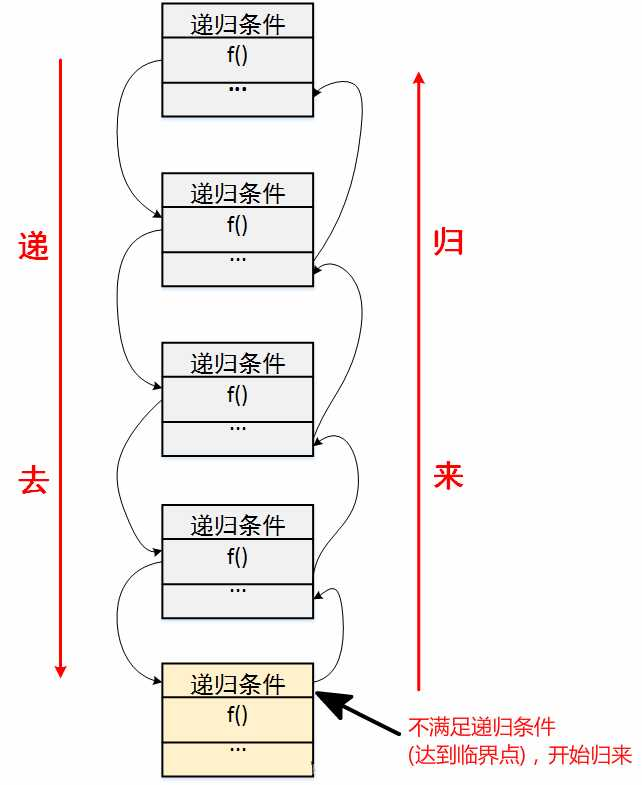
遞歸的本質就在：遞去，歸來 兩個流程中。 初學者剛接觸會有點抽象，下面通過一些案例來認識。

假設需要你實現一個階乘的計算函數，
階乘的定義：
5的階乘是 5*4*3*2*1=120

def factorial(number):
    if number == 1:
        return 1
    else:
        return number * factorial(number - 1)

print(factorial(5))
// 120

遞歸需要考慮三個條件：

1. 將問題拆分成一個重復使用的子問題；
2. 注意，這個子問題和問題的規模無關；
3. 必須包含終止條件 (終止條件即初始狀態)。

遞歸的底層實現（不是重點）

遞歸的底層實現不是本文的重點，了解一下就行。

遞歸在編程語言的底層實現通常依賴于調用棧（call stack）：

• 調用棧：

  • 每次函數調用時，程序會將函數的參數、局部變量和返回地址等信息壓入棧幀。
  • 當遞歸函數調用自身時，會創建新的棧幀壓入棧中。
  • 函數執行完畢后，棧幀被彈出，返回控制權給調用者。

• 基線條件：

  • 遞歸必須有終止條件，否則會導致棧溢出（stack overflow）。
  • 每次遞歸調用都應該向基線條件靠近。

• 內存管理：

  • 調用棧通常在內存的“棧區”分配。棧的大小有限制，過多的遞歸調用可能導致棧溢出。
  • 有些語言提供機制來增加棧的大小，但一般不推薦依賴深層遞歸。

總結：

• 遞歸實現的效率和安全性與具體語言的特性和編譯器的優化密切相關。

• 遞歸的底層實現，就是把相關變量數據（緩存）處理后，一層一層的壓入棧，等到了基準條件后，在逐層拿出處理。

計算機眼里的遞歸：
計算機使用棧來記錄正在調用的函數，叫調用棧。

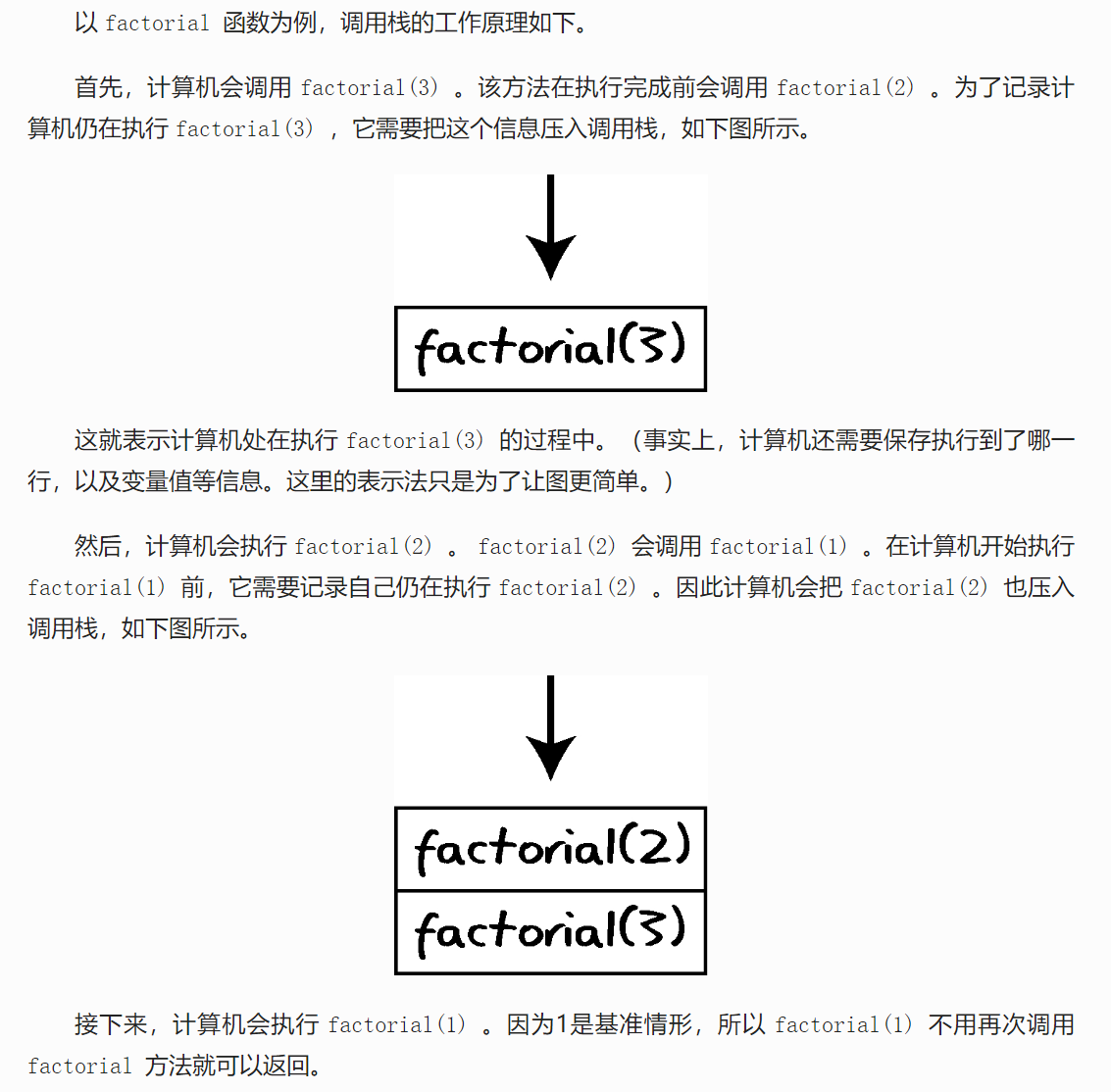
有個局部變量 number 記錄當前值。

遞歸的應用場景

• 處理任意多層事情的場景，都可以考慮用遞歸。

• 當問題和子問題具有遞推關系，比如楊輝三角、計算階乘。

• 具有遞歸性質的數據結構，比如鏈表、樹、圖。

• 反向性問題，比如取反操作。

編程中 兩種解決問題的思維

這個才是本文重點要學習的。

當面對未來未知的情況時，考慮使用使用自上而下解決問題的思維。

兩種編寫計算函數的方法:

• 自下而上(Bottom - Up)
  類似循環
• 自上而下 (Top - Down)
  遞歸思想

兩者區別？
在計算函數時，自下而上和自上而下是兩種不同的思維方式和實現策略：

在計算函數時，特別是像階乘這樣的遞歸函數，可以使用兩種主要的實現方式來實現遞歸計算：自下而上（bottom-up）和自上而下（top-down）。這些方法各有優缺點，理解它們有助于選擇適合的實現方式來解決特定的問題。以下是對這兩種實現方式的解釋：

自下而上（Bottom-Up）

自下而上方法，也稱為 迭代方法 或 動態規劃方法，是指從最小的子問題開始逐步構建解決方案，直到解決原始問題。這種方法通常用于動態規劃算法中，但也可以用于一些簡單的遞歸問題。

實現思路：

1. 定義最小問題: 從問題的最小子問題開始解決。例如，在計算階乘時，可以從 0! 或 1! 開始。
2. 逐步構建: 使用迭代或循環逐步計算更大的問題的解。
3. 更新和存儲: 將每個子問題的解存儲起來，以便后續使用。

還是以計算階乘的案例去介紹，自下而上實現方式：

def factorial_bottom_up(n):
    if n < 0:
        raise ValueError("Factorial is not defined for negative numbers")
    result = 1
    for i in range(2, n + 1):
        result *= i
    return result

# 示例用法
print(factorial_bottom_up(5))  # 輸出 120

解釋：

• 從 1 開始迭代計算 2 到 n 的階乘。
• 通過逐步乘以每個數字來更新結果，最終得到 n!。

自上而下（Top-Down）

自上而下方法也稱為 遞歸方法，是指從解決問題的最上層開始，遞歸地解決較小的子問題。這種方法在處理遞歸問題時非常自然（但可能存在重復計算的子問題，有些可以優化）。

實現思路：

1. 定義主問題: 從問題的最上層開始解決。
2. 遞歸分解: 將主問題遞歸地分解為較小的子問題。
3. 基本情況: 定義遞歸的基本情況，以停止遞歸。

還是以計算階乘的案例，展示自上而下實現：

def factorial_top_down(n):
    if n < 0:
        raise ValueError("Factorial is not defined for negative numbers")
    if n == 0 or n == 1:
        return 1
    return n * factorial_top_down(n - 1)

# 示例用法
print(factorial_top_down(5))  # 輸出 120

解釋：

• 從 n 開始，遞歸調用 factorial_top_down(n - 1)，直到達到基本情況。
• 在基本情況時返回 1，逐層返回乘積結果。

總結

• 自下而上：通常是迭代的方法，逐步構建解決方案，適用于動態規劃和需要避免重復計算的情況。它通常較為高效，尤其是在解決子問題重復計算時。

• 自上而下：通常是遞歸的方法，直觀地解決問題，但可能會有較高的時間復雜度和空間復雜度，尤其在處理大規模問題時。(可以通過記憶化（Memoization）來優化性能)

自上而下的思考過程——求和案例

一般來說，自下而上的實現過程比較好理解，所以這里多列舉一些自上而下的案例幫助思考，

自上而下的編程思考過程：

1. 把你正在寫的函數想象成是別人實現過的函數。
2. 辨別子問題。
3. 看看你在子問題上調用函數時會發生什么，然后以此為基礎繼續。

求和案例
假設我們要寫一個 sum 函數，計算數組中所有數的和。如果給函數傳入數組[1，2，3，4，5]，那么它會返回這些數的和15。

我們需要做的第一件事就是想象已經有人實現了 sum 函數。（當然，你可能會有點難以接受，畢竟寫函數是我們自己，怎么能假設別人寫好了呢！ 但可以試著忘掉這一點，先假裝 sum 函數已經實現好了。）

接下來，來辨別子問題。比起科學，這個過程更像是藝術，只要你多練習就能進步。 在這個例子中，可以認為子問題是數組[2，3，4，5]，即原數組中除第一個數以外的元素。

最后，來看看在子問題上調用 sum 函數會發生什么 ？
如果 sum 函數“已被正確實現”并且子問題是 [2，3，4，5]，那么調用 sum([2，3，4，5])時會發生什么呢?會得到2+3+4+5的和，也就是14。

而要求[1，2，3，4，5]的和，只需向 sum([2，3，4，5])的結果再加上1即可。

請使用編程語言實現一下：

mylist = [1, 2, 3, 4, 5]
def mysum(alist):

    if len(alist) == 1:
        return alist[0]
    else:
		# alist[-1] = alist[len(alist)-1]
        alist[0] += alist[-1]

    return mysum(alist[0:len(alist) - 1])

print(mysum(mylist))
# 15

臺階問題 案例

為什么需要用遞歸？

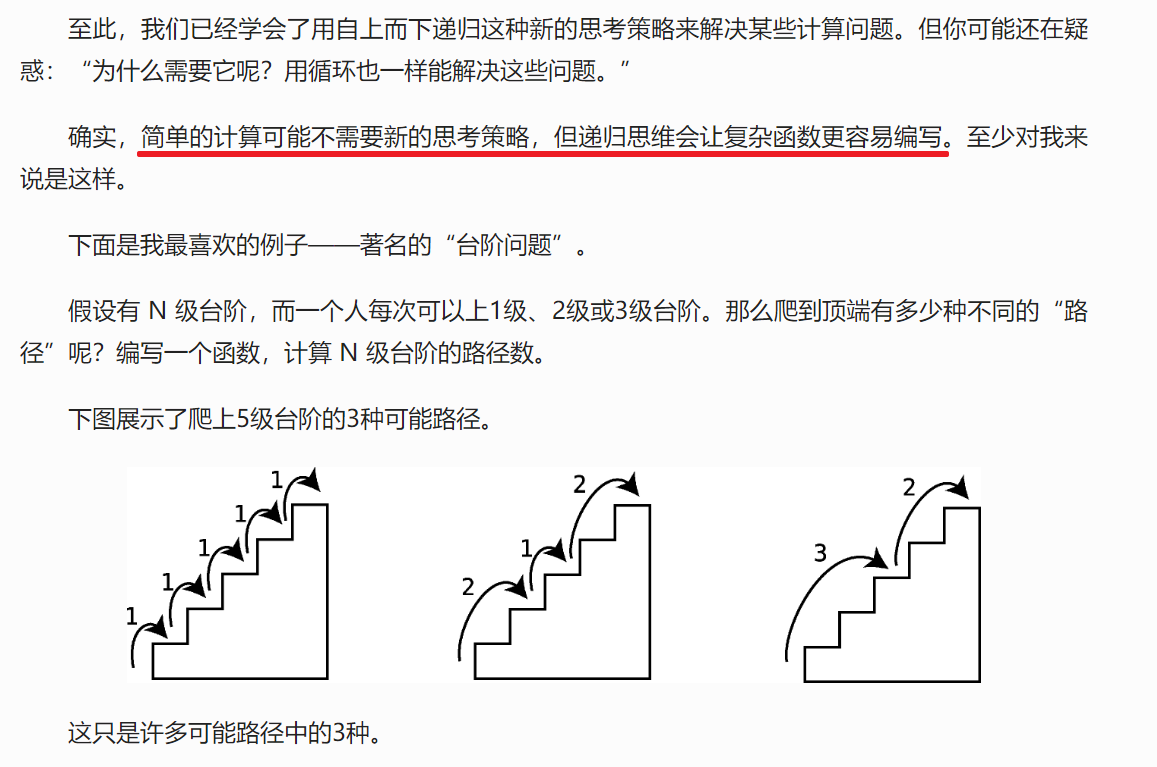
請寫出代碼：

todo

易位構詞生成 案例

這個是一個很實用的案例，之前想將多個pyload 以不同位置組合成一個整體，就遇到這個難題。

請寫出代碼：

todo