算法復雜度
時間復雜度: 常對冪指階
時間復雜度
時間復雜度指輸入數據大小為 N 時,算法運行所需花費的時間。統計的是算法的「計算操作數量」,而不是「運行的絕對時間」。
時間復雜度具有「最差」、「平均」、「最佳」三種情況,分別使用 O ,Θ ,Ω 三種符號表
常見種類: O(1)<O(logN)<O(N)<O(N*logN)<O(N2)<O(2n)<O(N!)
N2 :如冒泡排序
指數階常出現于遞歸
階乘階對應數學上常見的 “全排列”
對數階與指數階相反,指數階為 “每輪分裂出兩倍的情況” ,而對數階是 “每輪排除一半的情況” 。對數階常出現于「二分法」、「分治」等算法中,體現著 “一分為二” 或 “一分為多” 的算法思想。
線性對數階(N*logN)常出現于排序算法,例如「快速排序」、「歸并排序」、「堆排序」等
空間復雜度
通常情況下,空間復雜度指在輸入數據大小為 N 時,算法運行所使用的「暫存空間」+「輸出空間」的總體大小。
而根據不同來源,算法使用的內存空間分為三類:
指令空間:編譯后,程序指令所使用的內存空間。
數據空間:算法中的各項變量使用的空間,包括:聲明的常量、變量、動態數組、動態對象等使用的內存空間。
棧幀空間:程序調用函數是基于棧實現的,函數在調用期間,占用常量大小的棧幀空間,直至返回后釋放。棧幀空間的累計常出現于遞歸調用
常見種類:O(1)<O(logN)<O(N)<O(N2)<O(2N)
acwing模板
基礎算法
排序
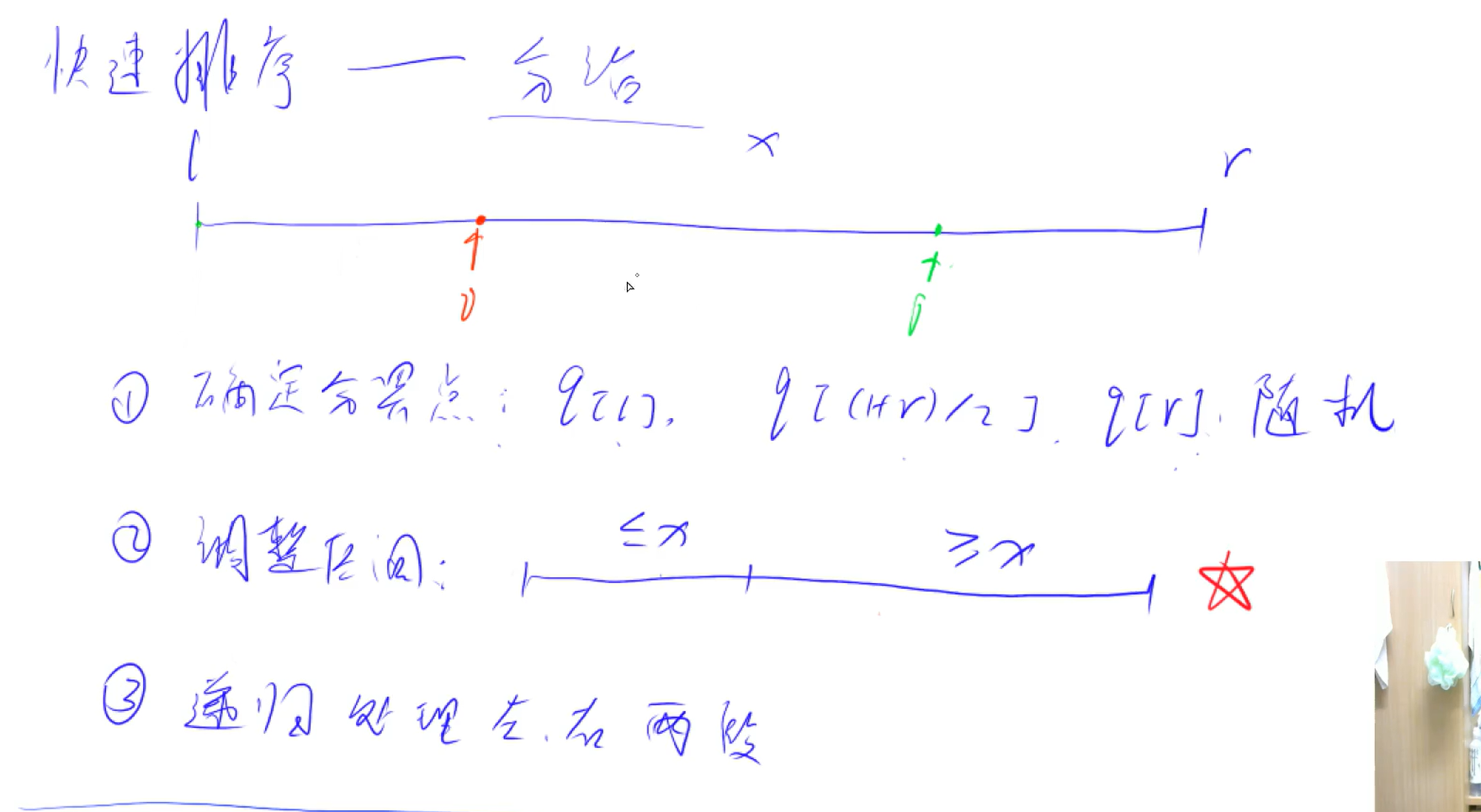
快速排序
快速排序是不穩定的
關鍵:在于如何劃分為兩個序列
時間復雜度:O(n logn)
const int N = 1e6 + 10;
int q[N];
int n;
void quick_sort(int q[], int l, int r){//l是左邊界,r是右邊界
if(l >= r) return;//當l和r相遇時,交換l和r位置
int x = q[l + r >> 1];//定義一個中間值,用于比較,把q[]分成大于和小于兩部分,更新了數據,不能用最左邊和最右邊了
int i = l-1, j = r+1;
while(i < j){
do i++; while(q[i] < x);
do j--; while(q[j] > x);
if( i < j ) swap(q[i],q[j]);//如果兩個數滿足在q[]的分別在另一邊,交換位置
}
quick_sort(q,l, j);
quick_sort(q, j + 1, r);//兩側迭代,直到有序
}
歸并排序
歸并排序是穩定的
關鍵:在于如何合并連個有序序列,雙路歸并,合二為一
時間復雜度:O(n logn)

const int N = 1e6 + 10;
int n;
int a[N],tmp[N];
void merge_sort(int q[], int l, int r){
if(l >= r) return;
//確定分界點
int mid = l + r >>1;
//遞歸分成左右兩段
merge_sort(q,l,mid);
merge_sort(q, mid+1, r);
int k = 0, i = l, j = mid + 1;
while(i <= mid&&j <= r){//判斷是否結束遍歷
if(q[i] <= q[j]) tmp[k++] = q[i++];
else tmp[k++] = q[j++];
}
while(i <= mid) tmp[k++] = q[i++];
while(j <= r) tmp[k++] = q[j++];
//把tmp臨時數組再賦值回去
for(int i = l, k = 0; i <= r; i++){
q[i] = tmp[k++];
}
}
快速排序和歸并排序區別
1.速排序是原地排序,原地排序指的是空間復雜度為O(1);
2.歸并排序不是原地排序,因為兩個有序數組的合并需要額外的空間協助才能合并;
3.快速排序是不穩定的,時間復雜度在O(nlogn)~O(n2)之間 。歸并排序是穩定的,時間復雜度是O(nlogn)。
4.快速排序是二叉樹模型
5.歸并排序是到二叉樹模型
二分
有序元素(有某種性質)+查找 == 二分
整數二分
二分的本質不是單調性,是二段性,將區間一分為二,一半滿足,一半不滿足

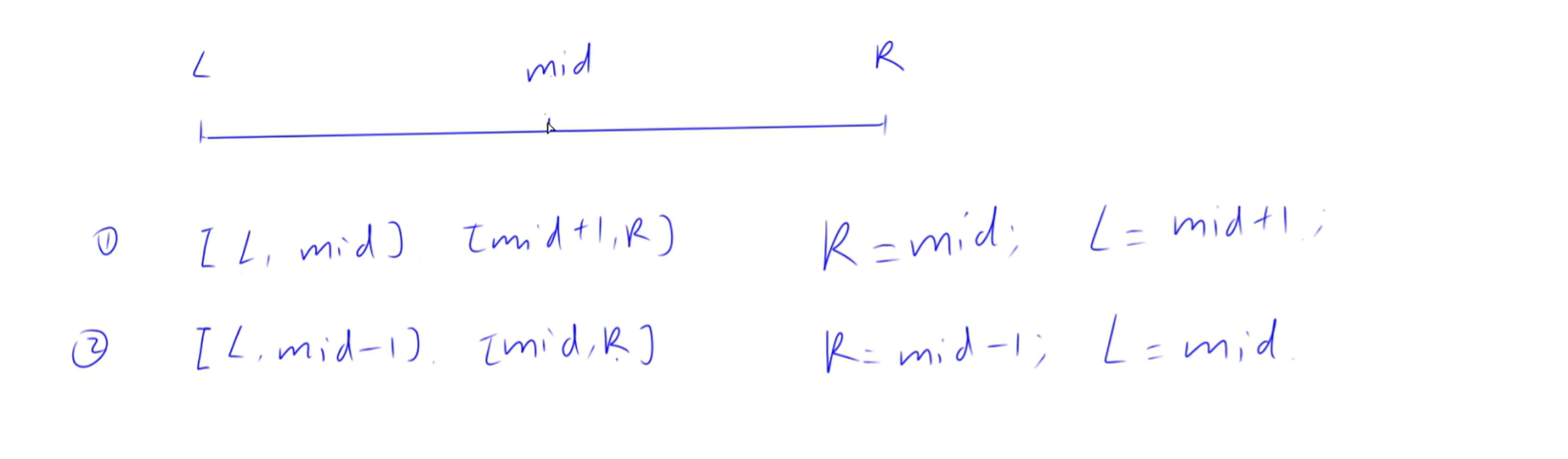
找分界點位置,分為兩種,
第一種,找紅色邊界點,l = mid,而且mid = l+r+1 >>1
第二種,找綠色邊界點,r = mid,mid = l + r >> 1
int l = 0, r = n-1;
bool check(int x) {/* ... */} // 檢查x是否滿足某種性質
// 區間[l, r]被劃分成[l, mid]和[mid + 1, r]時使用:
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid; // check()判斷mid是否滿足性質
else l = mid + 1;
}
return l;
}
// 區間[l, r]被劃分成[l, mid - 1]和[mid, r]時使用:
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
有點亂,看到還有一種方法,試試看
模板
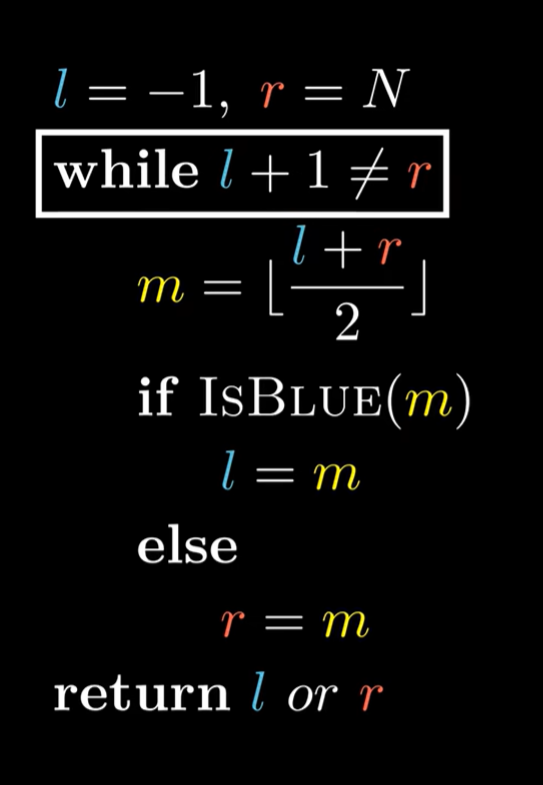

const int N = 1e6 + 10;
int q[N];
bool check(int x){
//要求數據的補集
if() return true;
return false;
}
int l = -1, r = n ;
while(l + 1 != r){
int mid = l + r >> 1;
if(check(q[mid])){
l = m;
}
else r = m;
}
這個方法,更容易出錯,返回l,r也有區別
浮點數二分
這個比較簡單,一般用于開方
int l = -100, r = 100;
while(r - l > 1e-6){//根據題目要求,一般情況下比題目保留位數大兩位
int mid = ( l + r ) / 2;
if(mid * mid >= x) r = m;//x為帶求開方數
else l = m;
}
高精度
高精度一般考四種
存儲方式用數組,倒序存,從個位存到高位
a + b 位數一般106

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
//加法
vector<int>add(vector<int>&A, vector<int> &B){//這里用引用避免了復制,節省了時間
vector<int>c;
int t = 0;//t表示進位
for(int i = 0; i < A.size()||i < B.size(); i++){
if(i < A.size()) t += A[i];
if(i < B.size()) t += B[i];
c.push_back(t%10);
t /= 10;
}
if(t != 0)
c.push_back(t);
return c;
}
int main()
{
string a,b;
vector<int>A,B;
cin>>a>>b;
//倒序存放到數組的過程
for(int i = a.size() - 1; i >= 0; i --) A.push_back(a[i] - '0');
for(int i = b.size() - 1; i >= 0; i --) B.push_back(b[i] - '0');
//加法
auto c = add(A,B);
//倒序取出
for(int i = c.size() - 1 ; i >= 0; i --){
printf("%d",c[i]);
}
return 0;
}
a - b 位數一般106
t表示借位
#include <iostream>
#include <string>
#include <vector>
using namespace std;
const int N = 1e5 + 10;
//判斷a >= b
bool cmp(vector<int> &a, vector<int> &b){
if(a.size() != b.size()) return a.size() > b.size();
for(int i = a.size() -1; i >= 0; i--){
//找到一位不同數字
if(a[i] != b[i])
return a[i] > b[i];
}
return true;
}
//c = a - b
vector<int> sub(vector<int> &a, vector<int> &b){
vector<int> c;
for(int i = 0, t = 0; i < a.size(); i++){
//t表示借位
t = a[i] - t;
//判斷b還有數字
if(i < b.size()) t -= b[i];
//原本要分為兩種情況,t > 0 和 t < 0, 這樣處理直接不需要分
c.push_back((t + 10) % 10);
if(t < 0) t = 1;//表明要借位
else t = 0;
}
while (c.size() > 1 && c.back() == 0) c.pop_back();
return c;
}
int main()
{
string n,m;
cin>>n>>m;
vector<int> a, b;
for(int i = n.size() - 1; i >= 0; i--) a.push_back(n[i] - '0');
for(int j = m.size() - 1; j >= 0; j--) b.push_back(m[j] - '0');
vector<int>c; // 存結果
//如果a>b
if(cmp(a,b)) {
c = sub(a,b);
}
else c = sub(b, a), cout<<"-";
//輸出
for(int i = c.size() - 1; i >= 0; i--){
cout<<c[i];
}
cout<<endl;
return 0;
}
a * b 大整數乘以一個小整數len(a) ≤ 106 且b ≤ 106
把小的數字當做一個整體
#include <iostream>
#include <vector>
using namespace std;
// c = a * b
vector<int> mul(vector<int> &a, int b)
{
vector<int> c;
int t = 0; // 進位
for (int i = 0; i < a.size() || t; i++) // 當i沒有處理完,或者t不為0
{
if (i < a.size())
t += a[i] * b;
c.push_back(t % 10);
t /= 10;
}
while(c.size() > 1&&c.back() == 0) c.pop_back();
return c;
}
int main()
{
string a;
int b;
cin >> a >> b;
vector<int> c;
for (int i = a.size() - 1; i >= 0; i--)
{
c.push_back(a[i] - '0');
}
auto s = mul(c, b);
for (int i = s.size() - 1; i >= 0; i--)
{
cout << s[i];
}
return 0;
}
a / b 求商和余數 大整數除以一個小整數len(a) ≤ 106 且b ≤ 106
注意倒著存,正著算

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// a/b,商是c,余數是r
vector<int> div(vector<int> &a, int b, int &r)
{
vector<int> c;
r = 0;
// 注意這里是正著的算的,但是a是倒著存的,所以如下
for (int i = a.size() - 1; i >= 0; i--)
{
r = r * 10 + a[i];
c.push_back(r / b);
r %= b;
}
//翻轉過來,正著除,倒著存,翻轉過來
reverse(c.begin(), c.end());
// 去掉前導0
while (c.size() > 1 && c.back() == 0)
c.pop_back();
return c;
}
int main()
{
string a;
int b;
cin >> a >> b;
vector<int> c;
for (int i = a.size() - 1; i >= 0; i--)
{
c.push_back(a[i] - '0');
}
int r;
auto s = div(c, b, r);
for (int i = s.size() - 1; i >= 0; i--)
{
cout << s[i];
}
cout << endl<< r;
return 0;
}
前綴和
一維前綴和
前綴和一定要下標從1開始,快速求出數組中一段數的和,sum[0] = 0;
const int N = 100001;
int sum[N],a[N];
for(int i = 1; i <= n; i++){
sum[i] = sum[i-1] + a[i];
}
int ans = sum[r] - sum[l-1];
詢問是O(1),預處理過程中是O(n)
對于二維矩陣的前綴和
const int N = 1010;
int sum[N][N],a[N][N];
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
cin>>a[i][j];
sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + a[i][j];
}
}
//(x2,y2) - (x1,y1);
int ans = sum[x2][y2] - sum[x2][y1-1] - sum[x1-1][y2] + sum[x1-1][y1-1];
差分
一維差分
構造一個b數組使得a是b的前n項和
#include<iostream>
using namespace std;
const int N = 100010;
int n,m;
int A[N],B[N];//b數組是a數組的差分,a數組是b數組的前綴和
void insert(int l, int r, int c){
B[l] += c;
B[r+1] -= c;
}
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= n;i++){//注意從一開始
scanf("%d",&A[i]);
}
for(int i = 1; i <= n; i++) insert(i,i, A[i]);
while(m--){
int l,r,c;
scanf("%d%d%d",&l,&r,&c);
insert(l,r,c);
}
for(int i = 1; i<= n; i++){
B[i] += B[i-1];
printf("%d ",B[i]);
}
return 0;
}
二維差分

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int A[N][N],B[N][N];
void insert(int x1, int y1, int x2, int y2, int c){
B[x1][y1] += c;
B[x2 + 1][y1] -= c;
B[x1][y2+1] -= c;
B[x2 + 1][ y2 + 1] += c;
}
int main(){
int n,m,q;
cin>>n>>m>>q;
for (int i = 1; i <= n; i ++ ){
for (int j = 1; j <= m; j ++ ){
cin>>A[i][j];
insert(i,j,i,j,A[i][j]);
}
}
while(q--){
int x1,y1,x2,y2,c;
cin>>x1>>y1>>x2>>y2>>c;
insert(x1,y1,x2,y2,c);
}
for(int i= 1; i <= n; i++){
for(int j = 1; j <= m; j++){
B[i][j] += B[i][j-1]+ B[i-1][j] - B[i-1][j-1];
printf("%d ",B[i][j]);
}
cout<<endl;
}
}
雙指針算法
找到某種單調性
可以把O(n2) 的算法優化成O(n)
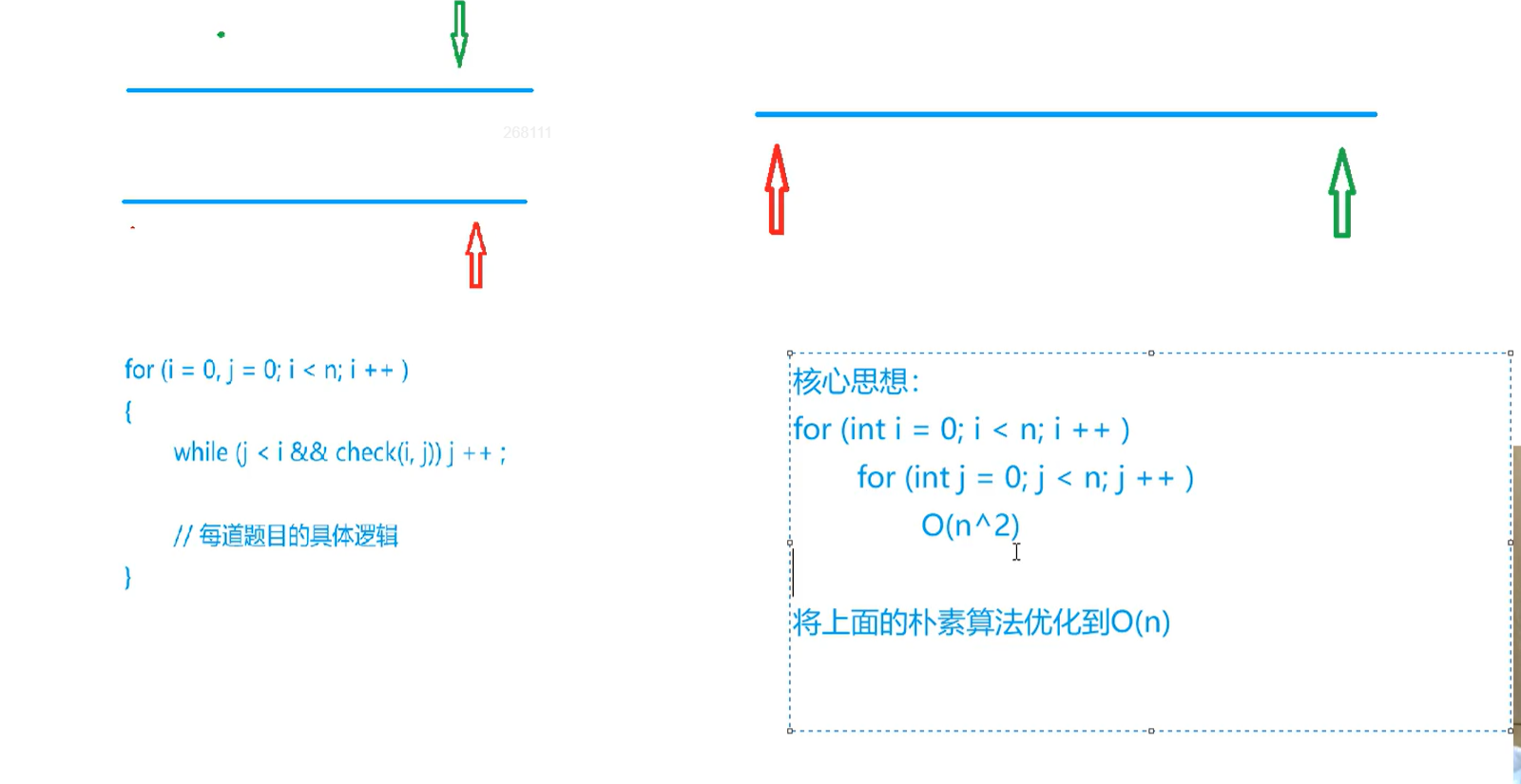
雙指針算法將暴力的優化一下
位運算
| 操作符 | 數字a | 數字b | 結果 |
|---|---|---|---|
| & | 0101 | 0001 | 0001 |
| 或 | 0101 | 0001 | 0101 |
| ~ | 0101 | 1010 | |
| ^ | 0101 | 0001 | 0100 |
| >>(右移) | /=2 | ||
| <<(左移) | *=2 |
n的二進制表示中,第k位是幾
先把k右移到最后一位 n >> k (n>>1 == n/=2)
在進行與運算 n & 1;
組合起來就是 n >> k & 1;
lowbit(x)是返回x的最后一位1是多少,可以用來統計x中1的個數
實現方式
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int lowbit(int x){
return x & -x;
}
int main(){
int n;
cin>>n;
while(n--){
int x;
cin>>x;
int res = 0;
while(x) {
x -= lowbit(x);//減去x中最后一位1
res++;
}
cout<<res <<' ';
}
return 0;
}
原碼:原來的 x
反碼:每一位取反 ~x
補碼:取反在加一 ~x+1
離散化
這里特指有序、飽序的數字的離散化
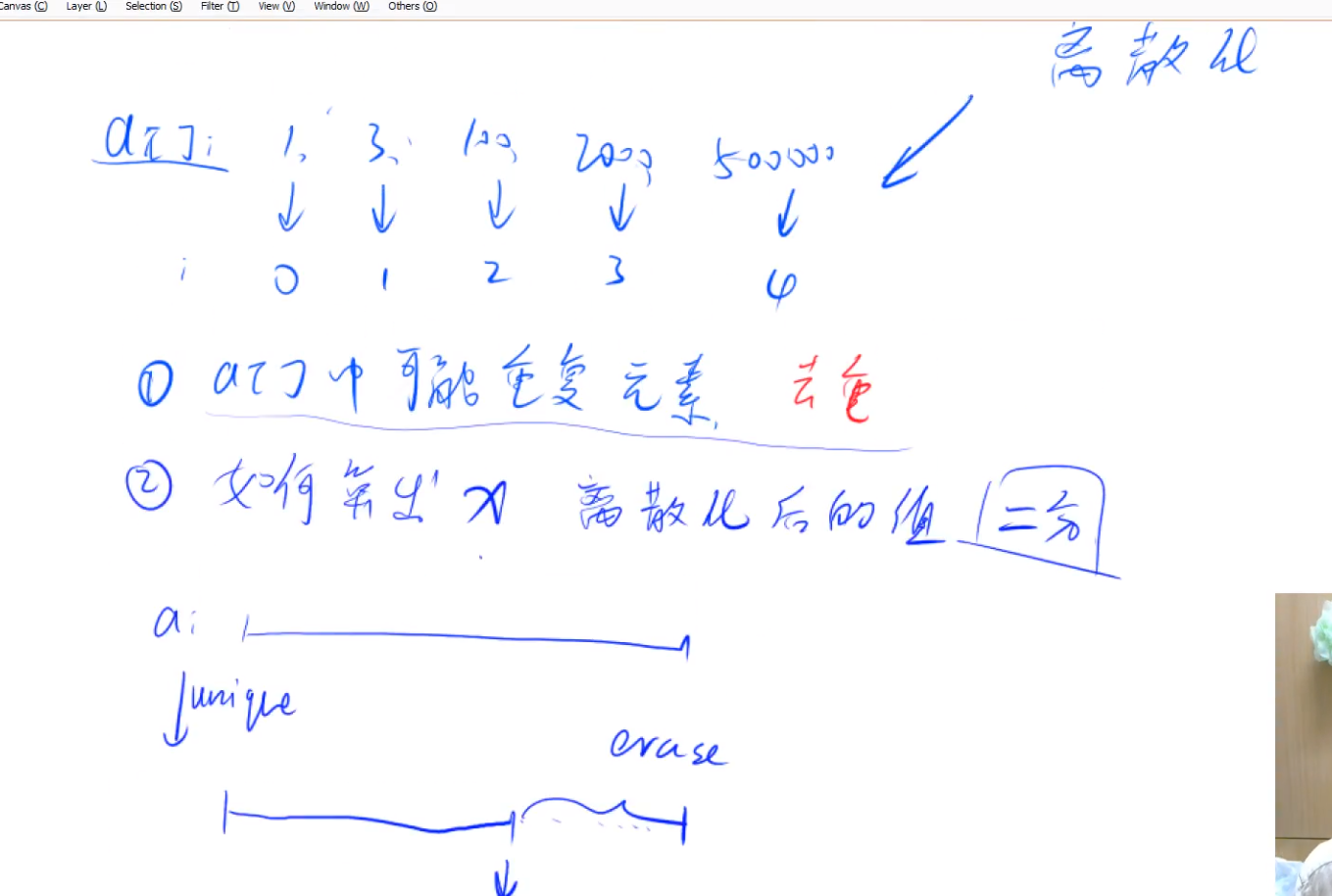
模板
vector<int> alls; // 存儲所有待離散化的值
sort(alls.begin(), alls.end()); // 將所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end()); // 去掉重復元素
// 二分求出x對應的離散化的值
int find(int x) // 找到第一個大于等于x的位置
{
int l = 0, r = alls.size() - 1;
while (l < r)
{
int mid = l + r >> 1;
if (alls[mid] >= x) r = mid;
else l = mid + 1;
}
return r + 1; // 映射到1, 2, ...n
}
unique實現

//a[j] 中存儲的就是不重復元素
vector<int>::iterator unique(vector<int> &a){
int j = 0;
for(int i = 0; i < a.size(); i++){
if(!a || a[i]!=a[i-1]){
a[j++] = a[i];
}
}
return a.begin() + j;
}
這是典例,區間和
#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 300010;
typedef pair<int, int> PII;
vector<int> alls;//存儲要離散化的位置
vector<PII> add,query;//插入操作,查詢
int a[N],s[N];//a是輸入的數,s是前綴和
//求x離散化后的結果,這里用到二分
int find(int x){
int l = 0;
int r = alls.size() - 1;
while(l < r){
int mid = l + r >> 1;
if(alls[mid] >= x) r = mid;//找大于等于x的最小值
else l = mid + 1;
}
return r + 1;//方便進行前綴和
}
int main(){
int n,m;
cin >> n >> m;
for (int i = 0; i < n; i++){
int x,c;
cin>>x>>c;
//在x的位置插入c
add.push_back({x,c});
alls.push_back(x);
}
for (int j = 0; j < m; j++){
int l,r;
cin>>l>>r;
query.push_back({l,r});
alls.push_back(l);
alls.push_back(r);
}
//去重alls
sort (alls.begin(),alls.end());
alls.erase(unique(alls.begin(),alls.end()), alls.end());
//處理插入
for(auto item : add){
int x = find(item.first);
a[x] += item.second;
}
//預處理前綴和
for(int i = 0; i <= alls.size(); i++){
s[i] = s[i-1] + a[i];
}
for(auto item : query){
int l = find(item.first);
int r = find(item.second);
cout<<s[r] - s[l -1]<<endl;
}
return 0;
}
區間合并

按照左端點進行排序
void merge(vector<PII> &segs)
{
vector<PII> res;
sort(segs.begin(), segs.end());
int st = -2e9, ed = -2e9;
for (auto seg : segs)
//沒有任何關系
if (ed < seg.first)
{
if (st != -2e9) res.push_back({st, ed});
st = seg.first, ed = seg.second;
}
//有關系,更新ed
else ed = max(ed, seg.second);
//把最后一個加入到區間里
if (st != -2e9) res.push_back({st, ed});
segs = res;
}
數據結構
鏈表與鄰接表:樹與圖的存儲
數組模擬單鏈表
主要是避免反復new結點,造成緩慢
用于存儲樹和圖
//head 表示頭指針
//e[i] 表示下標為i的結點的值
//next[i] 表示i的下一個結點
//idx 表示當前指導那個位置
int e[N],next[N],idx,head;
//初始化
void init(){
head = -1;
idx = 0;
}
//插入到頭結點
void add_to_head(int x){
e[idx] = x;
next[idx] = head;
head = idx;
idx ++;
}
//把x插入到下標為k的后面
void add(int k, int x){
e[idx] = x;
ne[idx] = ne[k];
ne[k] = idx;
idx++;
}
//單鏈表刪除k結點下一個元素
void remove(int k){
ne[k] = ne[ne[k]];
}
//雙向鏈表
int e[N],l[N],r[N],idx; //l[N]代表左側,r[N]代表右側
void init(){
idx = 2;
//兩個邊界
r[0] = 1;
l[1] = 0;
}
//在k右邊插入x
void add(int k, int x){
e[idx] = x;
l[idx] = k;
r[idx] = r[k];
l[r[k]] = idx;
r[k] = idx;
idx++;
}
//刪除第k個點
void remove(int k){
l[r[k]] = l[k];
r[l[k]] = r[k];
}
鄰接表是多個單列表
詳見第三章
棧與隊列:單調隊列、單調棧
// tt表示棧頂
int stk[N], tt = 0;
// 向棧頂插入一個數
stk[ ++ tt] = x;
// 從棧頂彈出一個數
tt -- ;
// 棧頂的值
stk[tt];
// 判斷棧是否為空,如果 tt > 0,則表示不為空
if (tt > 0)
{
}
單調棧
找某個數最左邊或者右邊距離他最近的大于或者小于他的數
常見模型:找出每個數左邊離它最近的比它大/小的數
int tt = 0;
for (int i = 1; i <= n; i ++ )
{
while (tt && check(stk[tt], i)) tt -- ;
stk[ ++ tt] = i;
}
時間復雜度O(n)
普通隊列
// hh 表示隊頭,tt表示隊尾
int q[N], hh = 0, tt = -1;
// 向隊尾插入一個數
q[ ++ tt] = x;
// 從隊頭彈出一個數
hh ++ ;
// 隊頭的值
q[hh];
// 判斷隊列是否為空,如果 hh <= tt,則表示不為空
if (hh <= tt)
{
}
循環隊列
// hh 表示隊頭,tt表示隊尾的后一個位置
int q[N], hh = 0, tt = 0;
// 向隊尾插入一個數
q[tt ++ ] = x;
if (tt == N) tt = 0;
// 從隊頭彈出一個數
hh ++ ;
if (hh == N) hh = 0;
// 隊頭的值
q[hh];
// 判斷隊列是否為空,如果hh != tt,則表示不為空
if (hh != tt)
{
}
單調隊列,滑動窗口
//常見模型:找出滑動窗口中的最大值/最小值
int hh = 0, tt = -1;
for (int i = 0; i < n; i ++ )
{
while (hh <= tt && check_out(q[hh])) hh ++ ; // 判斷隊頭是否滑出窗口
while (hh <= tt && check(q[tt], i)) tt -- ;
q[ ++ tt] = i;
}
原理差不多,等二刷
#include<iostream>
using namespace std;
const int N = 1000001;
int a[N], q[N];//q[N]存儲的是滑動窗口中的下標
int main(){
int n,k;
scanf("%d%d", &n,&k);
for(int i = 0; i < n; i++){
scanf("%d",&a[i]);
}
int hh = 0, tt = -1;
for(int i = 0; i < n; i++){
//判斷隊頭元素是否已經滑出窗口
if (hh <= tt && q[hh] < i - k + 1) hh++;
while(hh <= tt && a[q[tt]] >= a[i]) tt--;
q[++tt] = i;
if(i >= k -1) printf("%d ",a[q[hh]]);
}
puts("");
hh = 0, tt = -1;
for(int i = 0; i < n; i++){
if(hh <= tt && q[hh] < i - k + 1) hh++;
while(hh <= tt && a[q[tt]] <= a[i]) tt--;
q[++tt] = i;
if(i >= k - 1) printf("%d ", a[q[hh]]);
}
puts("");
return 0;
}
kmp
// s[]是長文本,p[]是模式串,n是s的長度,m是p的長度
求模式串的Next數組:
for (int i = 2, j = 0; i <= m; i ++ )
{
while (j && p[i] != p[j + 1]) j = ne[j];
if (p[i] == p[j + 1]) j ++ ;
ne[i] = j;
}
// 匹配
for (int i = 1, j = 0; i <= n; i ++ )
{
while (j && s[i] != p[j + 1]) j = ne[j];
if (s[i] == p[j + 1]) j ++ ;
if (j == m)
{
j = ne[j];
// 匹配成功后的邏輯
}
}
現在還不太懂代碼,但是原理懂了
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010, M = 1000010;
int n,m;
char p[N], s[M];
int nex[N];
int main(){
cin>>n>>p + 1>>m >> s+1;
for(int i = 2, j = 0; i <= n; i++){
while(j && p[i] != p[j + 1]) j = nex[j];
if(p[i] == p[j + 1]) j++;
nex[i] = j;
}
for(int i = 1, j = 0; i <= m; i++){
while(j && s[i] != p[j + 1]) j = nex[j];
if(s[i] == p[j + 1]) j++;
if(j == n){
printf("%d ", i- n);
j = nex[j];
}
}
return 0;
}
Trie
高效的存儲和查找字符串集合的數據結構
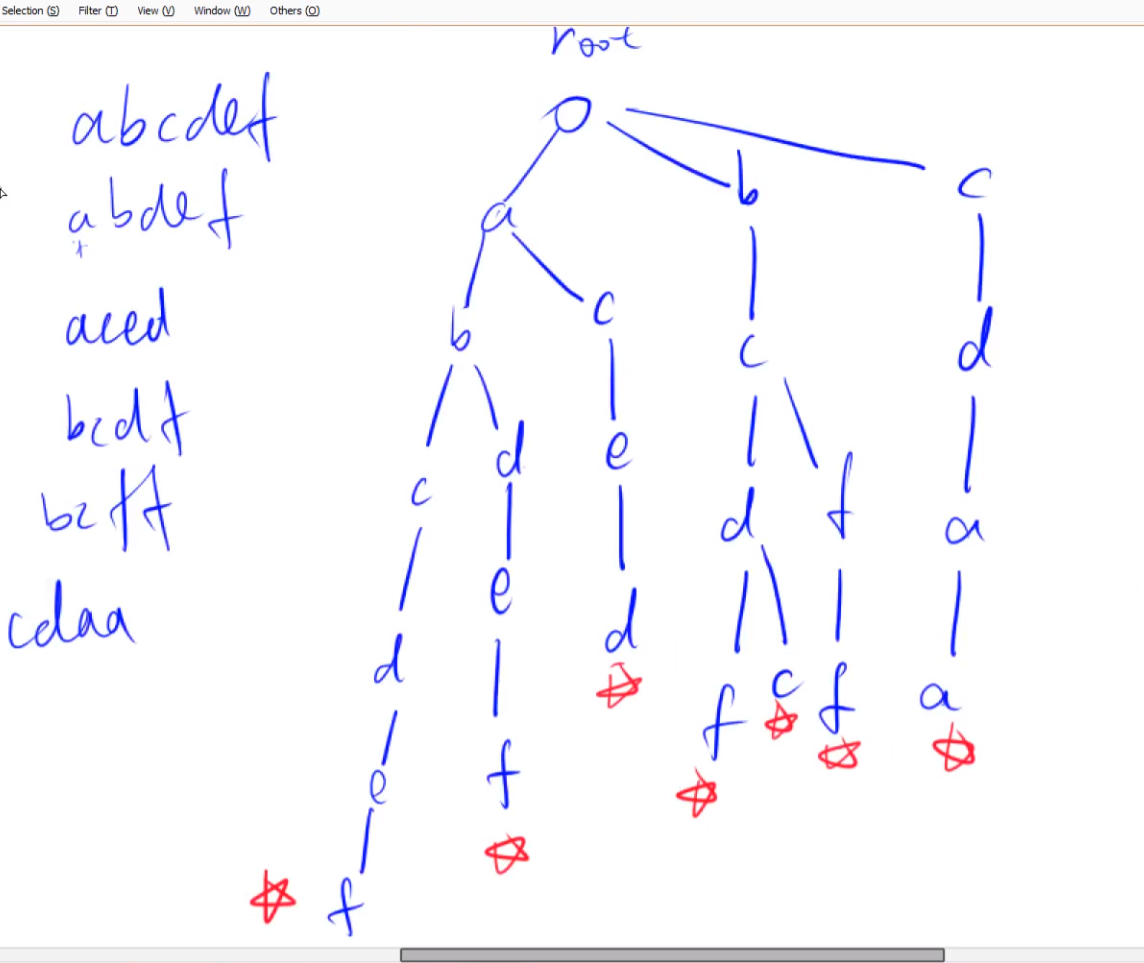
將所有字符串集合的結尾進行標記
int son[N][26], cnt[N], idx;
// 0號點既是根節點,又是空節點
// son[][]存儲樹中每個節點的子節點
// cnt[]存儲以每個節點結尾的單詞數量
// idx 存儲當前用到那個下標
// 插入一個字符串
void insert(char *str)
{
int p = 0;//從根節點開始遍歷
for (int i = 0; str[i]; i ++ )
{
int u = str[i] - 'a';//將a-z映射成0-25
if (!son[p][u]) son[p][u] = ++ idx;//如果不存在,就創建出來
p = son[p][u];//結束時對應的結尾位置為p
}
cnt[p] ++ ;
}
// 查詢字符串出現的次數
int query(char *str)
{
int p = 0;
for (int i = 0; str[i]; i ++ )
{
int u = str[i] - 'a';
if (!son[p][u]) return 0;
p = son[p][u];
}
return cnt[p];
}
并查集
兩個操作:(近乎O(1))
1.將兩個集合合并
2.詢問兩個元素是否在一個集合中
3.用樹的形式維護一個集合,根節點是他的代表元素,根節點的編號就是當前集合的編號,每個節點存儲他的父節點,p[x]表示x的父節點
4.判斷樹根p[x] = x
5.如何求x的集合編號:while(p[x] != x) x = p[x]
6.如何合并兩個集合:將一個集合當成另外一個集合的子節點p[x]是x的集合編號,p[y]是y的集合編號,p[x] = y
7.優化:
路徑壓縮一旦找到根節點,就將該路徑上的所有點都指向根節點,基本就可以看成O(1)
按秩合并:先留下,后面在補
(1)樸素并查集:
int p[N]; //存儲每個點的祖宗節點
// 返回x的祖宗節點
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// 初始化,假定節點編號是1~n
for (int i = 1; i <= n; i ++ ) p[i] = i;
// 合并a和b所在的兩個集合:
p[find(a)] = find(b);
// 查找是否在同一個集合
find(a) == find(b);
(2)維護size的并查集:
int p[N], size[N];
//p[]存儲每個點的祖宗節點, size[]只有祖宗節點的有意義,表示祖宗節點所在集合中的點的數量
// 返回x的祖宗節點
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// 初始化,假定節點編號是1~n
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
size[i] = 1;
}
// 合并a和b所在的兩個集合:這個有順序,不能錯
size[find(b)] += size[find(a)];
p[find(a)] = find(b);
(3)維護到祖宗節點距離的并查集:
int p[N], d[N];
//p[]存儲每個點的祖宗節點, d[x]存儲x到p[x]的距離
// 返回x的祖宗節點
int find(int x)
{
if (p[x] != x)
{
int u = find(p[x]);
d[x] += d[p[x]];
p[x] = u;
}
return p[x];
}
// 初始化,假定節點編號是1~n
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
d[i] = 0;
}
// 合并a和b所在的兩個集合:
p[find(a)] = find(b);
d[find(a)] = distance; // 根據具體問題,初始化find(a)的偏移量
堆
堆是維護一個數據集合,是用一維數組實現的完全二叉樹(常常用來構建優先隊列,支持堆排序,快速找出一個集合中的最小值或者最大值)
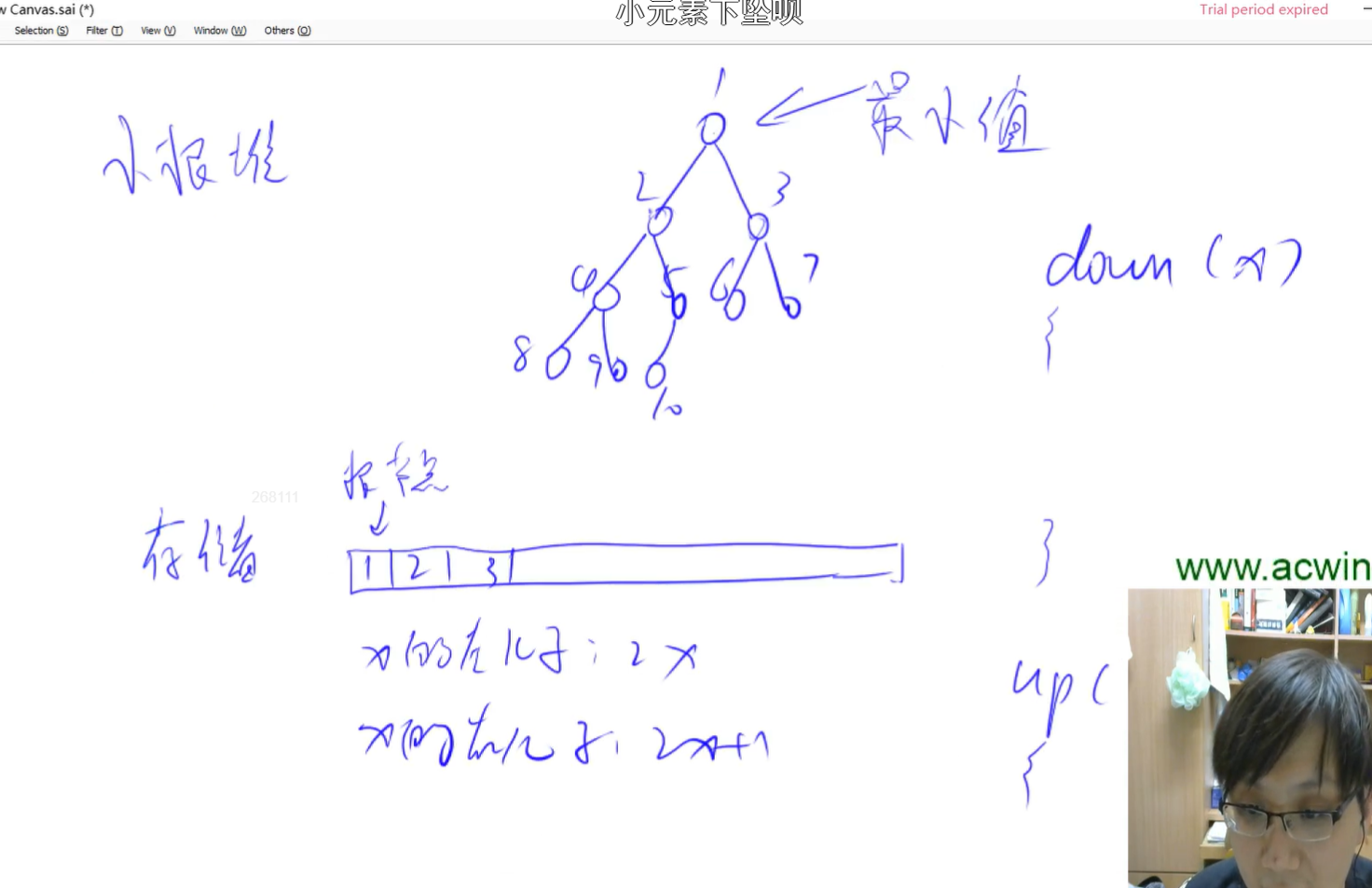
一維數組存貯
x的左兒子是2x
x的右兒子是2x+1
堆排序
這些操作都可以用down(){}和up(){}操作表示
down和up操作是O(logn),求最小值是O(1),插入和刪除都時O(logn)
將創建堆得操作從O(nlogn) 下降到 O(n),先插入n/2接下來的都down
Hash表
搜索和圖論
DFS與BFS
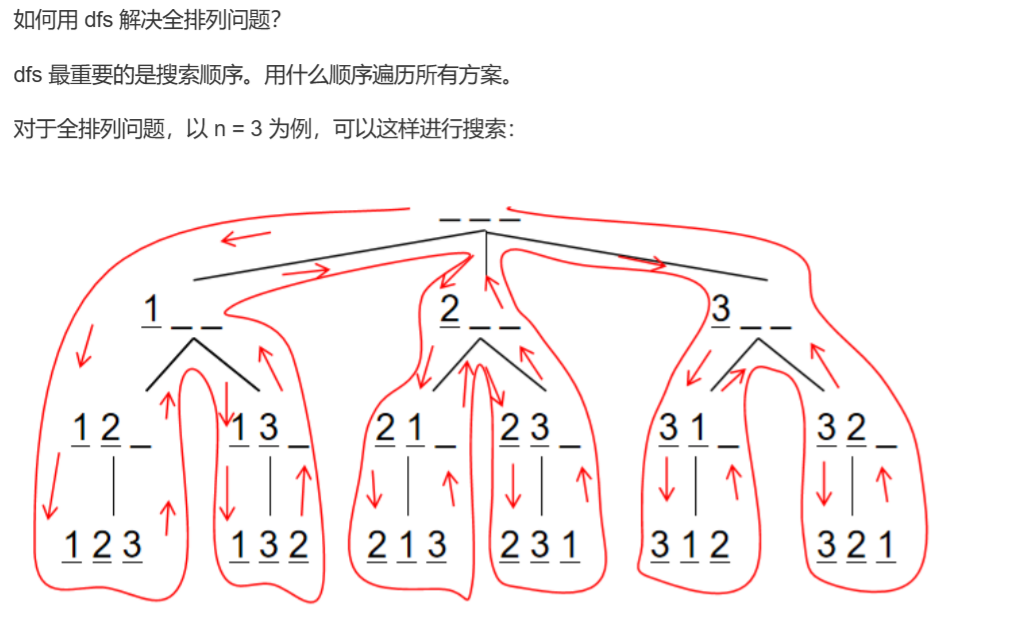
DFS
| 數據結構 | 空間 | 特點 | ||
|---|---|---|---|---|
| DFS | stack | O(h) | 不具有最短性 | 最重要的順序 |
| BFS | queue | O(2n) | 最短路 | |
| 剪枝: | ||||
| 最優性剪枝:不是最優解,剪枝 | ||||
| 可行性剪枝:不可行時候剪枝 |
BFS

/*
做這種題目的步驟(最短路問題)
1.創建兩個存儲,一個存儲值,一個存儲距離
2.然后首先將第一個點的位置存儲的距離提前標注出來
3.然后弄兩個方向變量用于上下左右前進int[] dx = {-1,0,1,0}, dy = {0,1,0,-1};
4.然后如果四個方向上的點沒有超過邊界,在結合實際情況有沒有用過的點,判斷能不能夠進行前進,如果可以就進行前進存儲其內容g跟距離d+1
5.最后返回想要的最短值d;
*/
樹與圖的遍歷:拓撲排序
樹是無環聯通的特殊的圖
圖:無向圖,有向圖
最短路
最小生成樹
二分圖:染色法、匈牙利算法
數學知識
質數
線性篩素數
const int N = 200000;
int primes[N];
int cnt = 0;
int heshu[N];
void get_primes(int n){
for(int i = 2; i < n; i++){
if(!heshu[i]) primes[cnt++] = i;
for(int j = 0; primes[j] * i <= n; j++){
heshu[primes[j] * i] = true;
if(i % primes[j] == 0) break;
}
}
}
1 ≤ n ≤ 106
時間復雜度O(n)
約數
int gcd(int a, int b)
{
return b ? gcd(b,a%b):a;
}
正常
int gcd(int a, int b){
if(a%b == 0) return b;
else return gcd(b,a%b);
}
歐拉函數
快速冪
快速冪迭代版
求ab mod p
typedef long long LL;
int quickmi(int a, int b, int p){//
int res = 1 %p;
while(b){//對b進行二進制化,從低位到高位
if(b & 1) res = (LL) res * a%p;
//更新a,a依次為a^{2^0},a^{2^1},a^{2^2},....,a^{2^logb}
a = (LL)a * a%p;
//b二進制右移一位
b >>= 1;
}
return res;
}
b&1就是判斷b的二進制表示中第0位上的數是否為1,若為1,b&1=true,反之b&1=false
b&1也可以用來判斷奇數和偶數,b&1=true時為奇數,反之b&1=false時為偶數
判斷二進制第k位的數字為1:n>>k&1 == true;
擴展歐幾里得算法
中國剩余定理
高斯消元
組合計數
Cbn = Cbn-1 + Cb-1n-1
const int N = 2001, MOD = 1e9+7;
typedef long long LL;
int C[N][N];
void init(int n){
for(int i = 0; i <= n; i++)
{
for(int j = 0; j <= i; j++){
if(j == 0){C[i][j] = 1;}
else C[i][j] = ((LL)C[i-1][j] + C[i-1][j-1])%MOD;
}
}
}
O(n2)
容斥原理

從n個數中選擇任意多個數的方案數,共有2n項,時間復雜度2n


for (int i = 1; i < 1 << m; i ++ )
// i<1<<m 組合數 2^m-1
{
//t表示所有質數的乘積,cnt表示i里面有幾個一
int t = 1, s = 0;
for (int j = 0; j < m; j ++ )//遍歷二進制的每一位
if (i >> j & 1)//判斷二進制第j位是否存在
{
if ((LL)t * p[j] > n)
{
t = -1;
break;
}
t *= p[j];
s ++ ;
}
if (t != -1)
{
if (s % 2) res += n / t;
else res -= n / t;
}
}






 浙公網安備 33010602011771號
浙公網安備 33010602011771號