線性模型與損失函數(shù)（分類問(wèn)題）

1.線性模型的構(gòu)成

??如下圖所示，這是一個(gè)基礎(chǔ)的線性模型示意圖。

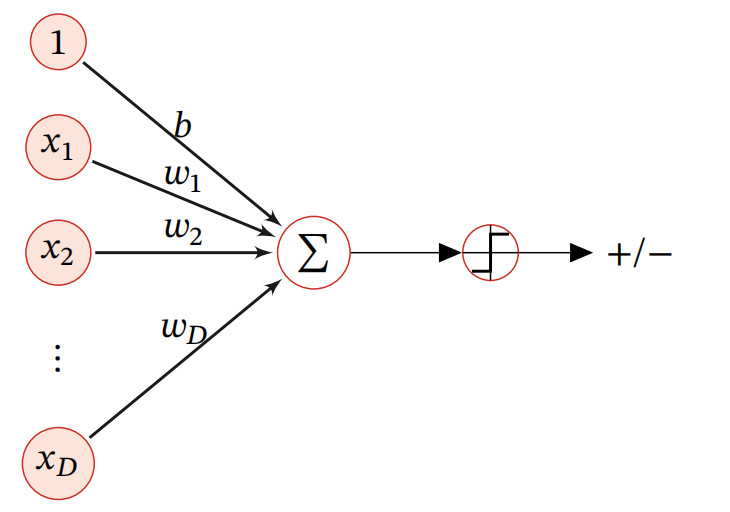
??線性模型是機(jī)器學(xué)習(xí)中應(yīng)用最廣泛的模型，指通過(guò)樣本特性的線性關(guān)系及組合來(lái)進(jìn)行預(yù)測(cè)的模型，我們用下式來(lái)表示線性模型函數(shù)（判別函數(shù)）一般的表現(xiàn)形式：

??其中，\(\mathop x\limits^ \to = {\left[ {{x_1}, \cdots ,{x_D}} \right]^T}\)是D維的樣本，\(\mathop \omega \limits^ \to = {\left[ {{\omega _1}, \cdots ,{\omega _D}} \right]^T}\)是\(D\)維的權(quán)重向量，\(b\)是偏置項(xiàng)，由于偏置項(xiàng)對(duì)整體來(lái)說(shuō)不是主要影響因素，所以我們將整體線性模型函數(shù)表示為\({f\left( {\mathop x\limits^ \to ;\mathop \omega \limits^ \to } \right)}\)。

??而在分類問(wèn)題中，我們的輸出的預(yù)計(jì)目標(biāo)是離散的標(biāo)簽（定義為\(y\)，即有\(y = f\left( {\mathop x\limits^ \to ;\mathop \omega \limits^ \to } \right)\)），而實(shí)際模型函數(shù)\({f\left( {\mathop x\limits^ \to ;\mathop \omega \limits^ \to } \right)}\)的輸出是實(shí)數(shù)，所以我們無(wú)法直接使用模型函數(shù)的輸出進(jìn)行預(yù)測(cè)，所以需要引入一個(gè)非線性的決策函數(shù)（等價(jià)于激活函數(shù)的作用）\(g\left( \bullet \right)\)來(lái)預(yù)測(cè)模型真實(shí)輸出，即\(y = g\left( {f\left( {\mathop x\limits^ \to ;\mathop \omega \limits^ \to } \right)} \right)\)。

2.線性判別函數(shù)、決策（等價(jià)與激活的作用）函數(shù)與決策邊界

2.1二分類

??在二分類模型中，\(y\)（我們預(yù)測(cè)所對(duì)比的標(biāo)簽）通常只有兩類值，即負(fù)值和正值，我們用\(\left\{ {-1,+1} \right\}\)來(lái)表示（也可以用\(\left\{ {1,0} \right\}\)），而且線性判別函數(shù)我們只需要一個(gè)就能分出兩個(gè)類別，即在特征空間中我們將所有滿足\(f\left( {x;\omega } \right) = 0\)的點(diǎn)構(gòu)成一個(gè)決策邊界，以此實(shí)現(xiàn)分成兩類的目的。

??在特征空間中，決策平面與權(quán)重向量\(\omega\)正交。而且在特征空間的每個(gè)點(diǎn)距決策平面的有向距離用下式表示：

??其中\(\gamma\)表示點(diǎn)\({\mathop x\limits^ \to }\)在\({\mathop \omega\limits^ \to }\)方向上的投影，為了更加直觀的看出這些效果，我們可以看到下圖：

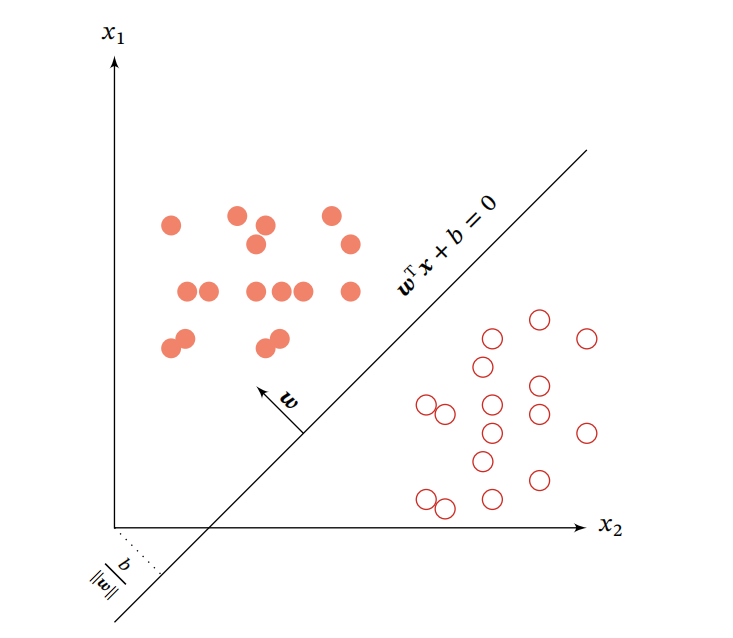
??圖中橫縱坐標(biāo)表示的是樣本的特征向量\(\mathop x\limits^ \to = \left[ {{x_1},{x_2}} \right]\)，權(quán)重向量\(\mathop \omega \limits^ \to = \left[ {{\omega _1},{\omega _2}} \right]\)，假設(shè)總共為N個(gè)樣本的訓(xùn)練集（包含數(shù)據(jù)和標(biāo)簽）\(D = \left\{ {\left( {\mathop {{x^{\left( n \right)}}}\limits^ \to ,{y^{\left( n \right)}}} \right)} \right\}_{n = 1}^N\)，其中\({y^{\left( n \right)}} \in \left\{ { + 1, - 1} \right\}\)，我們的線性模型要學(xué)到參數(shù)\(\mathop {{\omega ^ * }}\limits^ \to\)，使得\(\mathop {{\omega ^ * }}\limits^ \to\)要滿足\({y^{\left( n \right)}}f\left( {\mathop {{x^{\left( n \right)}}}\limits^ \to ;\mathop {{\omega ^ * }}\limits^ \to } \right) > 0,\forall n \in \left[ {1,N} \right]\)，即線性判別函數(shù)為正的時(shí)候?qū)?yīng)標(biāo)簽為正，同理，判別函數(shù)為負(fù)對(duì)應(yīng)標(biāo)簽也為負(fù)。

??那么問(wèn)題來(lái)了，這個(gè)參數(shù)\(\mathop \omega \limits^ \to\)我們的模型是怎么學(xué)習(xí)到的呢？

??這個(gè)問(wèn)題的答案也就是各種分類問(wèn)題不一樣的答案，即我們是通過(guò)損失函數(shù)讓線性預(yù)測(cè)模型學(xué)習(xí)參數(shù)\(\mathop \omega \limits^ \to\)，損失函數(shù)的不同也是區(qū)分各種分類模型最明顯的點(diǎn)。

??二分類的損失函數(shù)是0-1損失函數(shù)，即：

??其中，\(I\left( \bullet \right)\)是指示函數(shù)，但是0-1損失函數(shù)的數(shù)學(xué)性質(zhì)不好，其關(guān)于\(\mathop \omega \limits^ \to\)的導(dǎo)數(shù)為0，從而讓其無(wú)法繼續(xù)優(yōu)化。

2.2多分類

??多分類和二分類的區(qū)別主要有兩個(gè)，第一，多分類的決策邊界有多個(gè)（即，線性判別函數(shù)有多個(gè)）；第二，各種分類問(wèn)題的損失函數(shù)不同（即，模型學(xué)習(xí)參數(shù)\(\mathop \omega \limits^ \to\)的方式不同）。但是多分類與二分類又是緊密聯(lián)系的，因?yàn)槎喾诸悊?wèn)題可以拆分為多個(gè)二分類問(wèn)題。

??多分類問(wèn)題類別為\(\left\{ {1,2, \cdots ,C} \right\}\)，常用的有以下三類方式：

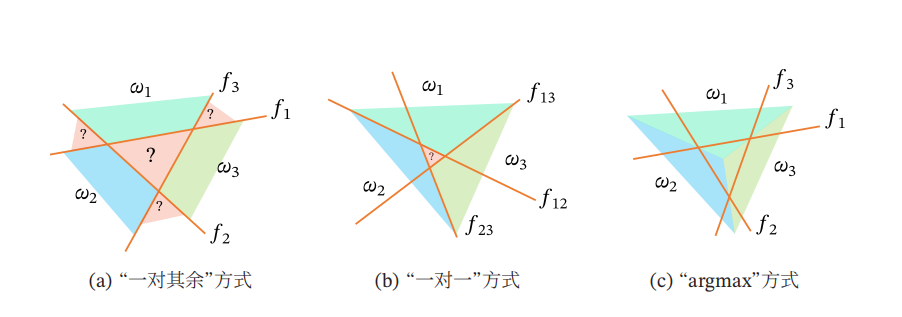
?（1）“一對(duì)其余”方式：把多分類問(wèn)題轉(zhuǎn)換為C個(gè)“一對(duì)其余”的二分類問(wèn)題。這種方式共需要C個(gè)判別函數(shù)，其中第c個(gè)判別函數(shù)\({f_c}\)是將類別c的樣本和不屬于該類別的樣本分開(kāi)。

?（2）“一對(duì)一”方式：把多分類問(wèn)題轉(zhuǎn)換為\(C\left( {C - 1} \right)/2\)個(gè)“一對(duì)一”的二分類問(wèn)題。這種方式共需要\(C\left( {C - 1} \right)/2\)個(gè)判別函數(shù)，其中第幾個(gè)判別函數(shù)就是將第幾個(gè)樣本進(jìn)行與其他樣本的拆分。

?（3）“argmax”方式：這是一種改進(jìn)的“一對(duì)其余”方式，共需要C個(gè)判別函數(shù)：

??對(duì)于樣本\({\mathop x\limits^ \to }\)，如果存在一個(gè)類別c，相對(duì)于所有的其他類別\(\mathop c\limits^ \sim\)有\({f_c}\left( {\mathop x\limits^ \to ;\mathop {{\omega _c}}\limits^ \to } \right) > {f_{\mathop c\limits^ \sim }}\left( {\mathop x\limits^ \to ;\mathop {{\omega _{\mathop c\limits^ \sim }}}\limits^ \to } \right)\)，那么\(\mathop x\limits^ \to\)屬于類別c。該種方式的預(yù)測(cè)函數(shù)定義為：

??如下圖所示，其中“argmax”對(duì)比于其它兩種方式具有明顯的優(yōu)勢(shì)，因?yàn)樗梢詼?zhǔn)確地判別任何一個(gè)樣本所屬的類別，而不會(huì)出現(xiàn)無(wú)法判別的問(wèn)題。

3.Logistic回歸（二分類方式）

??說(shuō)到Logistic回歸我們首先來(lái)看一下Logistic函數(shù)的定義，Logistic函數(shù)是一種常用的S型函數(shù)，其定義式為：

??其中，\(\exp \left( \bullet \right)\)表示自然對(duì)數(shù)，\({{x_0}}\)是中心點(diǎn)，\(L\)是最大值，\(K\)是曲線的傾斜度，為了更加直觀的看看logistic函數(shù)的性質(zhì)，我們看看它的效果圖：

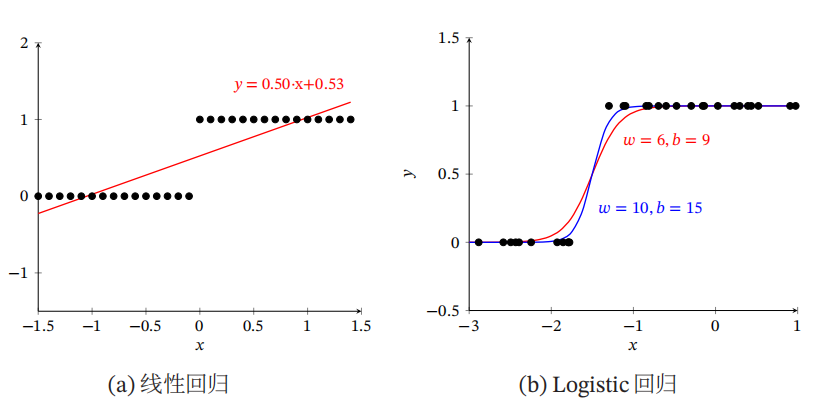
??有上圖我們可以看出，當(dāng)x趨向于\(- \infty\)時(shí)，\(\log istic\left( x \right)\)趨向于0；當(dāng)x趨向于\(+ \infty\)時(shí)，\(\log istic\left( x \right)\)趨向于L。并且當(dāng)參數(shù)為第一行即藍(lán)色實(shí)線時(shí)，\(\log istic\left( x \right)\)函數(shù)被稱為標(biāo)準(zhǔn)\(\log istic\left( x \right)\)函數(shù)，記作\(\sigma \left( x \right)\)。且\(\sigma \left( x \right) = \frac{1}{{1 + \exp \left( { - x} \right)}}\)。

??Logistic回歸也就是對(duì)數(shù)回歸，是一種常用的二分類問(wèn)題的線性模型，為了解決連續(xù)的線性函數(shù)不適合進(jìn)行分類的問(wèn)題，我們定義對(duì)數(shù)回歸為：

??其中，\(g\left( \bullet \right)\)稱為激活函數(shù)，作用是將線性函數(shù)的值域從實(shí)數(shù)區(qū)間壓縮到\(\left( {0,1} \right)\)之間，可以用來(lái)表示概率。

??在Logistic回歸中，我們使用Logistic函數(shù)來(lái)作為激活函數(shù)，標(biāo)簽y=1的后驗(yàn)概率為：

??其中，\(\mathop x\limits^ \to = {\left[ {{x_1}, \cdots ,{x_D},1} \right]^T}\)表示樣本的D+1維增廣特征向量\(\mathop \omega \limits^ \to = {\left[ {{\omega _1}, \cdots ,{\omega _D},b} \right]^T}\)表示D+1維的增廣權(quán)重向量。

??既然得到了y=1的后驗(yàn)概率，那么在二分類中y=0的后驗(yàn)概率很容易就可以得到：

??而\({\mathop {{\omega ^T}}\limits^ \to \mathop x\limits^ \to }\)可以表示為：

??其中，\(\frac{{p\left( {y = 1|\mathop x\limits^ \to } \right)}}{{p\left( {y = 0|\mathop x\limits^ \to } \right)}}\)為樣本正反例后驗(yàn)概率的比值，稱為幾率。

??下圖給出了線性回歸和Logistic回歸的區(qū)別：

3.1該種方式的參數(shù)學(xué)習(xí)

??Logistic回歸采用交叉熵作為損失函數(shù)，并使用梯度下降算法來(lái)進(jìn)行參數(shù)的優(yōu)化。

??給定N個(gè)訓(xùn)練樣本\(\left\{ {\mathop {{x^{\left( n \right)}}}\limits^ \to ,{y^{\left( n \right)}}} \right\}_{n = 1}^N\)，用對(duì)數(shù)回歸模型對(duì)每個(gè)樣本進(jìn)行預(yù)測(cè)，輸出其標(biāo)簽為1的后驗(yàn)概率，記為\({{\hat y}^{\left( n \right)}}\)，

??由于\({y^{\left( n \right)}} \in \left\{ {0,1} \right\}\)，樣本\(\left( {\mathop {{x^{\left( n \right)}}}\limits^ \to ,{y^{\left( n \right)}}} \right)\)的真實(shí)條件概率可以表示為：

??使用交叉熵?fù)p失函數(shù)，但是為了簡(jiǎn)單起見(jiàn)，忽略了正則化項(xiàng)，其風(fēng)險(xiǎn)函數(shù)為：

??由風(fēng)險(xiǎn)函數(shù)\(\Re \left( {\mathop \omega \limits^ \to } \right)\)對(duì)參數(shù)\({\mathop \omega \limits^ \to }\)的偏導(dǎo)數(shù)為：

??采用梯度下降算法，Logistic回歸的訓(xùn)練過(guò)程為：初始化\(\mathop {{\omega _0}}\limits^ \to \leftarrow 0\)，然后通過(guò)下式來(lái)迭代更新參數(shù)：

??其中，\(\alpha\)是學(xué)習(xí)率，\({\hat y_{{\omega _t}}^{\left( n \right)}}\)是當(dāng)參數(shù)為\(\mathop {{\omega _t}}\limits^ \to\)時(shí)，Logistic回歸模型的輸出。

4.Softmax回歸（多分類的對(duì)數(shù)回歸方式）

??Softmax回歸，是Logistic回歸在多分類問(wèn)題上的推廣。

??對(duì)于多分類問(wèn)題，類別標(biāo)簽\(y \in \left\{ {1,2, \cdots ,C} \right\}\)可以有\(C\)個(gè)取值，給定一個(gè)樣本\({\mathop x\limits^ \to }\)，那么Softmax回歸預(yù)測(cè)的屬于類別c的條件概率為：

??其中，\(\mathop {{\omega _c}}\limits^ \to\)是第c類的權(quán)重向量。

??softmax回歸的決策函數(shù)可以表示為：

??與Logistic回歸的關(guān)系表現(xiàn)為，當(dāng)類別數(shù)C=2時(shí)，Softmax回歸的決策函數(shù)為：

??其中，\(I\left( \bullet \right)\)是指示函數(shù)，所以根據(jù)二分類的線性模型我們可以得到權(quán)重向量的表達(dá)式為\(\mathop \omega \limits^ \to = \mathop {{\omega _1}}\limits^ \to - \mathop {{\omega _0}}\limits^ \to\)。

4.1參數(shù)學(xué)習(xí)

??首先，我們都是通過(guò)損失函數(shù)使得我們的模型進(jìn)行參數(shù)矩陣\(W\)學(xué)習(xí)的，而在softmax回歸模型中我們使用的是交叉熵?fù)p失函數(shù)，所以我們可以得到其風(fēng)險(xiǎn)函數(shù)為：

??其中，\({{\hat y}^{\left( n \right)}} = soft\max \left( {{W^T}\mathop {{x^{\left( n \right)}}}\limits^ \to } \right)\)為樣本\({\mathop {{x^{\left( n \right)}}}\limits^ \to }\)在每個(gè)類別的后驗(yàn)概率。

??風(fēng)險(xiǎn)函數(shù)\(\Re \left( W \right)\)關(guān)于W的梯度為：

??如果根據(jù)上式我們通過(guò)非向量形式轉(zhuǎn)變，可以得到下列式子：

??采用梯度下降法，softmax回歸的訓(xùn)練過(guò)程為：初始化\({W_0} \leftarrow 0\)，然后通過(guò)下式進(jìn)行更新迭代：

??其中\(\alpha\)是學(xué)習(xí)率，\({\hat y_{{W_t}}^{\left( n \right)}}\)是當(dāng)參數(shù)為\(\mathop {{W_t}}\limits^ \to\)時(shí)，Softmax回歸模型的輸出。