本文基于NumSharp用C#改寫了一個用python實現的簡單線性回歸，通過這次實踐，可以加深對線性回歸原理的理解，也可以練習使用NumSharp。

前言

最近注意到了NumSharp，想學習一下，最好的學習方式就是去實踐，因此從github上找了一個用python實現的簡單線性回歸代碼，然后基于NumSharp用C#進行了改寫。

NumSharp簡介

NumSharp（NumPy for C#）是一個在C#中實現的多維數組操作庫，它的設計受到了Python中的NumPy庫的啟發。NumSharp提供了類似于NumPy的數組對象，以及對這些數組進行操作的豐富功能。它是一個開源項目，旨在為C#開發者提供在科學計算、數據分析和機器學習等領域進行高效數組處理的工具。

python代碼

用到的python代碼來源：llSourcell/linear_regression_live: This is the code for the "How to Do Linear Regression the Right Way" live session by Siraj Raval on Youtube (github.com)

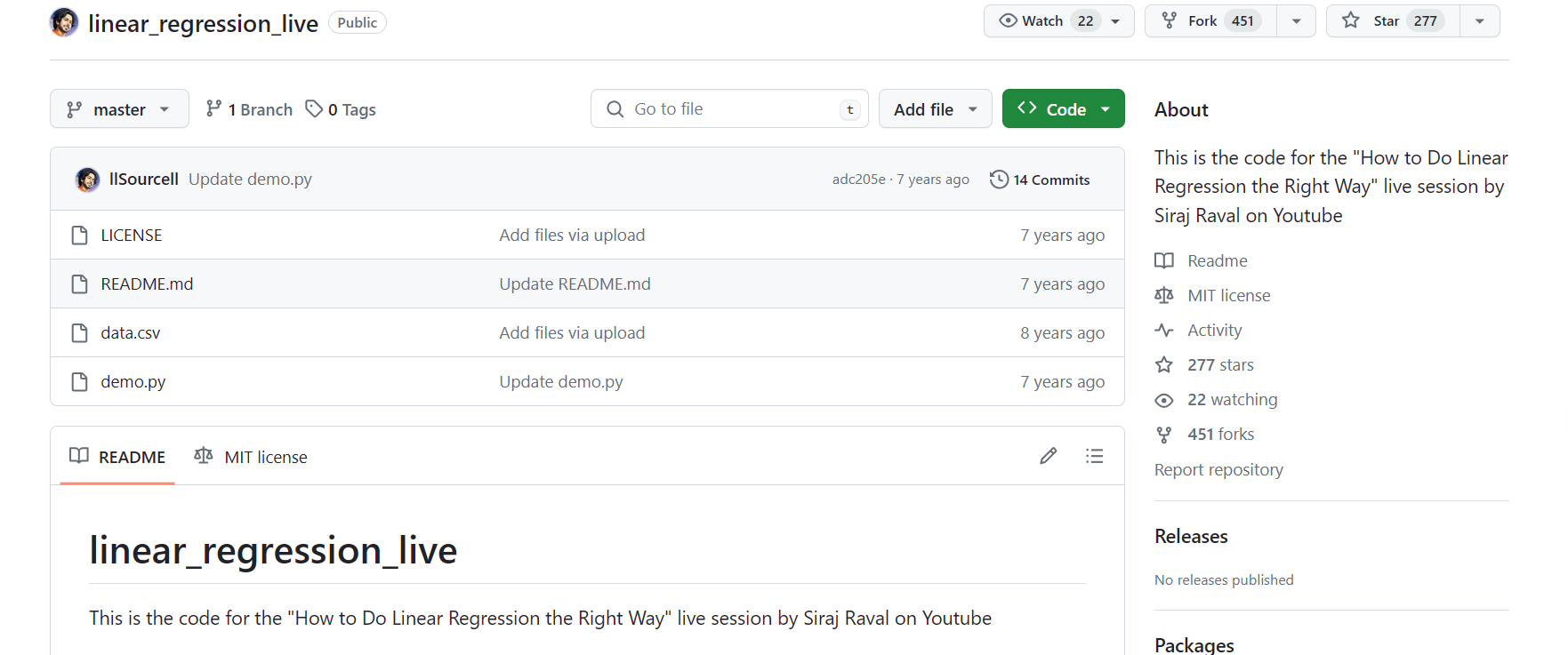
下載到本地之后，如下圖所示：

python代碼如下所示：

#The optimal values of m and b can be actually calculated with way less effort than doing a linear regression. 
#this is just to demonstrate gradient descent
?
from numpy import *
?
# y = mx + b
# m is slope, b is y-intercept
def compute_error_for_line_given_points(b, m, points):
    totalError = 0
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        totalError += (y - (m * x + b)) ** 2
    return totalError / float(len(points))
?
def step_gradient(b_current, m_current, points, learningRate):
    b_gradient = 0
    m_gradient = 0
    N = float(len(points))
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        b_gradient += -(2/N) * (y - ((m_current * x) + b_current))
        m_gradient += -(2/N) * x * (y - ((m_current * x) + b_current))
    new_b = b_current - (learningRate * b_gradient)
    new_m = m_current - (learningRate * m_gradient)
    return [new_b, new_m]
?
def gradient_descent_runner(points, starting_b, starting_m, learning_rate, num_iterations):
    b = starting_b
    m = starting_m
    for i in range(num_iterations):
        b, m = step_gradient(b, m, array(points), learning_rate)
    return [b, m]
?
def run():
    points = genfromtxt("data.csv", delimiter=",")
    learning_rate = 0.0001
    initial_b = 0 # initial y-intercept guess
    initial_m = 0 # initial slope guess
    num_iterations = 1000
    print ("Starting gradient descent at b = {0}, m = {1}, error = {2}".format(initial_b, initial_m, compute_error_for_line_given_points(initial_b, initial_m, points)))
    print ("Running...")
    [b, m] = gradient_descent_runner(points, initial_b, initial_m, learning_rate, num_iterations)
    print ("After {0} iterations b = {1}, m = {2}, error = {3}".format(num_iterations, b, m, compute_error_for_line_given_points(b, m, points)))
?
if __name__ == '__main__':
    run()

用C#進行改寫

首先創建一個C#控制臺應用，添加NumSharp包：

現在我們開始一步步用C#進行改寫。

python代碼：

points = genfromtxt("data.csv", delimiter=",")

在NumSharp中沒有genfromtxt方法需要自己寫一個。

C#代碼：

 //創建double類型的列表
 List<double> Array = new List<double>();
?
 // 指定CSV文件的路徑
 string filePath = "你的data.csv路徑";
?
 // 調用ReadCsv方法讀取CSV文件數據
 Array = ReadCsv(filePath);
?
 var array = np.array(Array).reshape(100,2);
?
static List<double> ReadCsv(string filePath)
{
    List<double> array = new List<double>();
    try
    {
        // 使用File.ReadAllLines讀取CSV文件的所有行
        string[] lines = File.ReadAllLines(filePath);             
?
        // 遍歷每一行數據
        foreach (string line in lines)
        {
            // 使用逗號分隔符拆分每一行的數據
            string[] values = line.Split(',');
?
            // 打印每一行的數據
            foreach (string value in values)
            {
                array.Add(Convert.ToDouble(value));
            }                  
        }
    }
    catch (Exception ex)
    {
        Console.WriteLine("發生錯誤: " + ex.Message);
    }
    return array;
}

python代碼：

def compute_error_for_line_given_points(b, m, points):
    totalError = 0
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        totalError += (y - (m * x + b)) ** 2
    return totalError / float(len(points))

這是在計算均方誤差:

C#代碼：

 public static double compute_error_for_line_given_points(double b,double m,NDArray array)
 {
     double totalError = 0;
     for(int i = 0;i < array.shape[0];i++)
     {
         double x = array[i, 0];
         double y = array[i, 1];
         totalError += Math.Pow((y - (m*x+b)),2);
     }
     return totalError / array.shape[0];
 }

python代碼：

def gradient_descent_runner(points, starting_b, starting_m, learning_rate, num_iterations):
    b = starting_b
    m = starting_m
    for i in range(num_iterations):
        b, m = step_gradient(b, m, array(points), learning_rate)
    return [b, m]

def step_gradient(b_current, m_current, points, learningRate):
    b_gradient = 0
    m_gradient = 0
    N = float(len(points))
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        b_gradient += -(2/N) * (y - ((m_current * x) + b_current))
        m_gradient += -(2/N) * x * (y - ((m_current * x) + b_current))
    new_b = b_current - (learningRate * b_gradient)
    new_m = m_current - (learningRate * m_gradient)
    return [new_b, new_m]

這是在用梯度下降來迭代更新y = mx + b中參數b、m的值。

因為在本例中，誤差的大小是通過均方差來體現的，所以均方差就是成本函數（cost function）或者叫損失函數（loss function），我們想要找到一組b、m的值，讓誤差最小。

成本函數如下：

對θ1求偏導，θ1就相當于y = mx + b中的b：

再對θ2求偏導，θ2就相當于y = mx + b中的m：

使用梯度下降：

θ1與θ2的表示：

α是學習率，首先θ1、θ2先隨機設一個值，剛開始梯度變化很大，后面慢慢趨于0，當梯度等于0時，θ1與θ2的值就不會改變了，或者達到我們設置的迭代次數了，就不再繼續迭代了。關于原理這方面的解釋，可以查看這個鏈接（Linear Regression in Machine learning - GeeksforGeeks），本文中使用的圖片也來自這里。

總之上面的python代碼在用梯度下降迭代來找最合適的參數，現在用C#進行改寫：

 public static double[] gradient_descent_runner(NDArray array, double starting_b, double starting_m, double learningRate,double num_iterations)
 {
     double[] args = new double[2];
     args[0] = starting_b;
     args[1] = starting_m;
?
     for(int i = 0 ; i < num_iterations; i++) 
     {
         args = step_gradient(args[0], args[1], array, learningRate);
     }
?
     return args;
 }

 public static double[] step_gradient(double b_current,double m_current,NDArray array,double learningRate)
 {
     double[] args = new double[2];
     double b_gradient = 0;
     double m_gradient = 0;
     double N = array.shape[0];
?
     for (int i = 0; i < array.shape[0]; i++)
     {
         double x = array[i, 0];
         double y = array[i, 1];
         b_gradient += -(2 / N) * (y - ((m_current * x) + b_current));
         m_gradient += -(2 / N) * x * (y - ((m_current * x) + b_current));
     }
?
     double new_b = b_current - (learningRate * b_gradient);
     double new_m = m_current - (learningRate * m_gradient);
     args[0] = new_b;
     args[1] = new_m;
?
     return args;
 }

用C#改寫的全部代碼：

using NumSharp;
?
namespace LinearRegressionDemo
{
    internal class Program
    {    
        static void Main(string[] args)
        {   
            //創建double類型的列表
            List<double> Array = new List<double>();
?
            // 指定CSV文件的路徑
            string filePath = "你的data.csv路徑";
?
            // 調用ReadCsv方法讀取CSV文件數據
            Array = ReadCsv(filePath);
?
            var array = np.array(Array).reshape(100,2);
?
            double learning_rate = 0.0001;
            double initial_b = 0;
            double initial_m = 0;
            double num_iterations = 1000;
?
            Console.WriteLine($"Starting gradient descent at b = {initial_b}, m = {initial_m}, error = {compute_error_for_line_given_points(initial_b, initial_m, array)}");
            Console.WriteLine("Running...");
            double[] Args =gradient_descent_runner(array, initial_b, initial_m, learning_rate, num_iterations);
            Console.WriteLine($"After {num_iterations} iterations b = {Args[0]}, m = {Args[1]}, error = {compute_error_for_line_given_points(Args[0], Args[1], array)}");
            Console.ReadLine();
?
        }
?
        static List<double> ReadCsv(string filePath)
        {
            List<double> array = new List<double>();
            try
            {
                // 使用File.ReadAllLines讀取CSV文件的所有行
                string[] lines = File.ReadAllLines(filePath);             
?
                // 遍歷每一行數據
                foreach (string line in lines)
                {
                    // 使用逗號分隔符拆分每一行的數據
                    string[] values = line.Split(',');
?
                    // 打印每一行的數據
                    foreach (string value in values)
                    {
                        array.Add(Convert.ToDouble(value));
                    }                  
                }
            }
            catch (Exception ex)
            {
                Console.WriteLine("發生錯誤: " + ex.Message);
            }
            return array;
        }
?
        public static double compute_error_for_line_given_points(double b,double m,NDArray array)
        {
            double totalError = 0;
            for(int i = 0;i < array.shape[0];i++)
            {
                double x = array[i, 0];
                double y = array[i, 1];
                totalError += Math.Pow((y - (m*x+b)),2);
            }
            return totalError / array.shape[0];
        }
?
        public static double[] step_gradient(double b_current,double m_current,NDArray array,double learningRate)
        {
            double[] args = new double[2];
            double b_gradient = 0;
            double m_gradient = 0;
            double N = array.shape[0];
?
            for (int i = 0; i < array.shape[0]; i++)
            {
                double x = array[i, 0];
                double y = array[i, 1];
                b_gradient += -(2 / N) * (y - ((m_current * x) + b_current));
                m_gradient += -(2 / N) * x * (y - ((m_current * x) + b_current));
            }
?
            double new_b = b_current - (learningRate * b_gradient);
            double new_m = m_current - (learningRate * m_gradient);
            args[0] = new_b;
            args[1] = new_m;
?
            return args;
        }
?
        public static double[] gradient_descent_runner(NDArray array, double starting_b, double starting_m, double learningRate,double num_iterations)
        {
            double[] args = new double[2];
            args[0] = starting_b;
            args[1] = starting_m;
?
            for(int i = 0 ; i < num_iterations; i++) 
            {
                args = step_gradient(args[0], args[1], array, learningRate);
            }
?
            return args;
        }
?
?
    }
}

python代碼的運行結果：

C#代碼的運行結果：

結果相同，說明改寫成功。

總結

本文基于NumSharp用C#改寫了一個用python實現的簡單線性回歸，通過這次實踐，可以加深對線性回歸原理的理解，也可以練習使用NumSharp。