基于EM期望最大化算法的GMM參數(shù)估計與三維數(shù)據(jù)分類系統(tǒng)python源碼
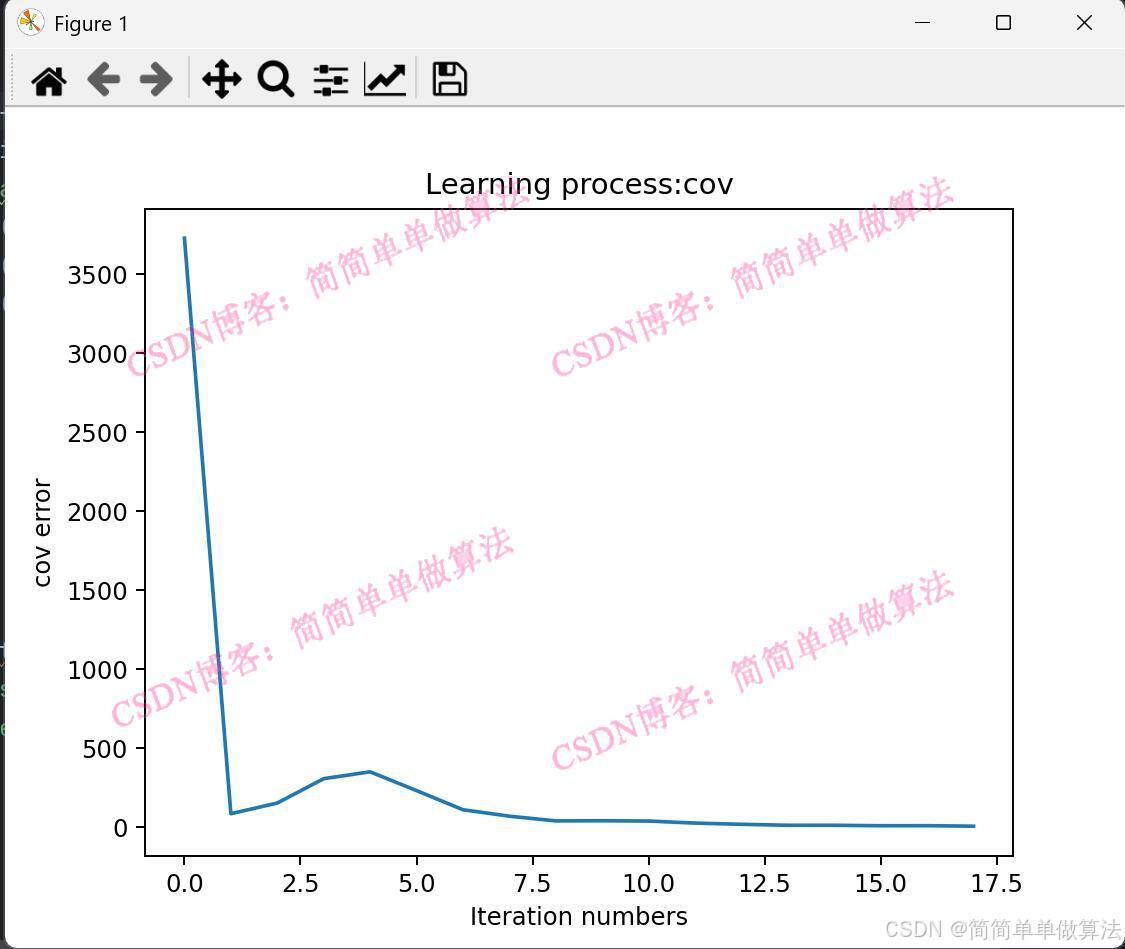
1.算法運行效果圖預(yù)覽
(完整程序運行后無水印)
2.算法運行軟件版本
程序運行配置環(huán)境:
人工智能算法python程序運行環(huán)境安裝步驟整理-CSDN博客
3.部分核心程序
(完整版代碼包含部分中文注釋和操作步驟視頻)
for z in range(k):
err += (abs(Old_mu[z, 0] - mu[z, 0]) + abs(Old_mu[z, 1] - mu[z, 1]) + abs(Old_mu[z, 2] - mu[z, 2])) # 計算誤差
err_alpha += abs(Old_alpha[z] - alpha_[z])
err_cov += abs(Old_cov[z,0,0] - sigma4_[z,0,0])+abs(Old_cov[z,0,1] - sigma4_[z,0,1])+abs(Old_cov[z,0,2] - sigma4_[z,0,2])+abs(Old_cov[z,1,0] - sigma4_[z,1,0])+abs(Old_cov[z,1,1] - sigma4_[z,1,1])+abs(Old_cov[z,1,2] - sigma4_[z,1,2])+abs(Old_cov[z,2,0] - sigma4_[z,2,0])+abs(Old_cov[z,2,1] - sigma4_[z,2,1])+abs(Old_cov[z,2,2] - sigma4_[z,2,2])
if (err <= 0.001) and (err_alpha < 0.001): # 達(dá)到精度退出迭代
print(err, err_alpha)
break
Learn_process[i] = err;
alpha_process[i] = err_alpha;
cov_process[i] = err_cov;
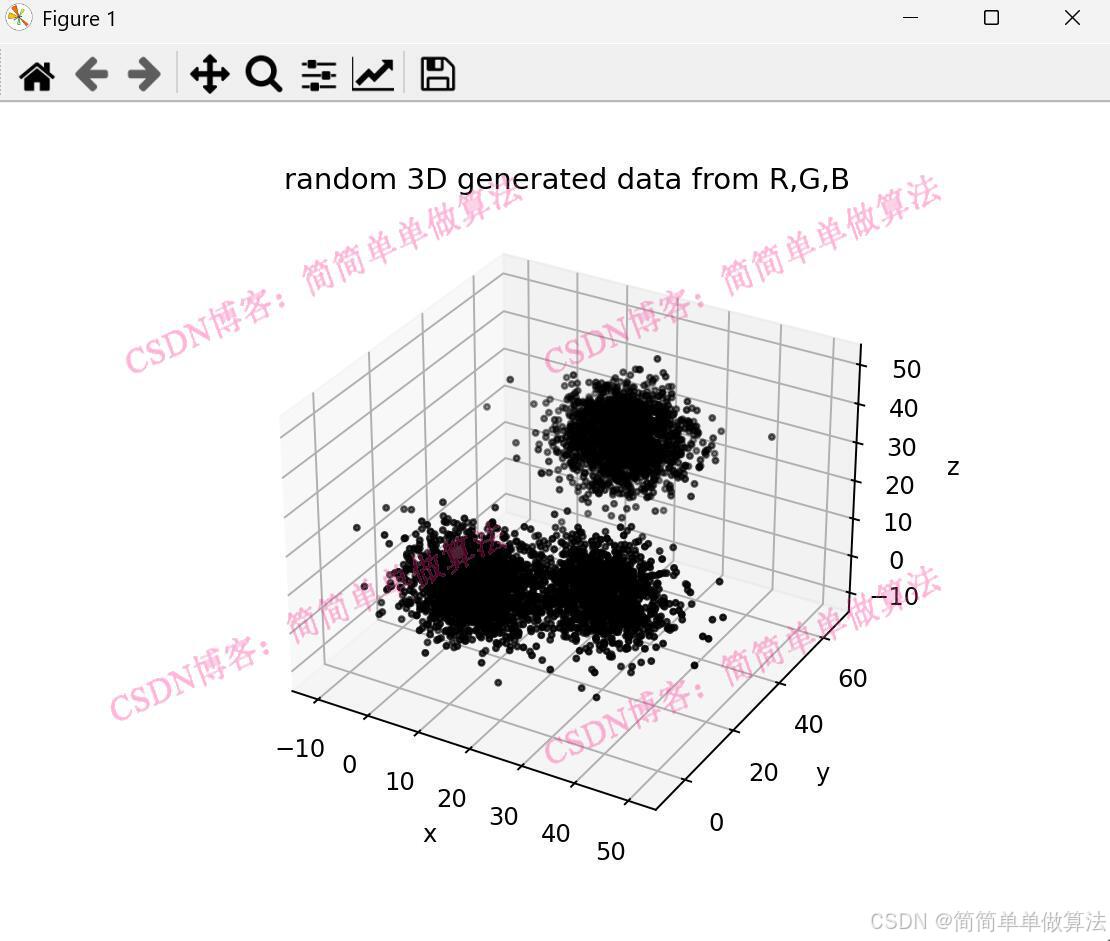
print("observable data:\n", X) # 輸出可觀測樣本
order = np.zeros(N)
color = ['b', 'r', 'y']
ax = plt.figure().add_subplot(111, projection='3d')
for i in range(N):
for j in range(k):
if excep[i, j] == max(excep[i, :]):
order[i] = j # 選出X[i,:]屬于第幾個高斯模型
probility[i] += alpha_[int(order[i])] * math.exp(-(X[i, :] - mu[j, :]) * sigma.I * np.transpose(X[i, :] - mu[j, :])) / (np.sqrt(np.linalg.det(sigma)) * 2 * np.pi) # 計算混合高斯分布
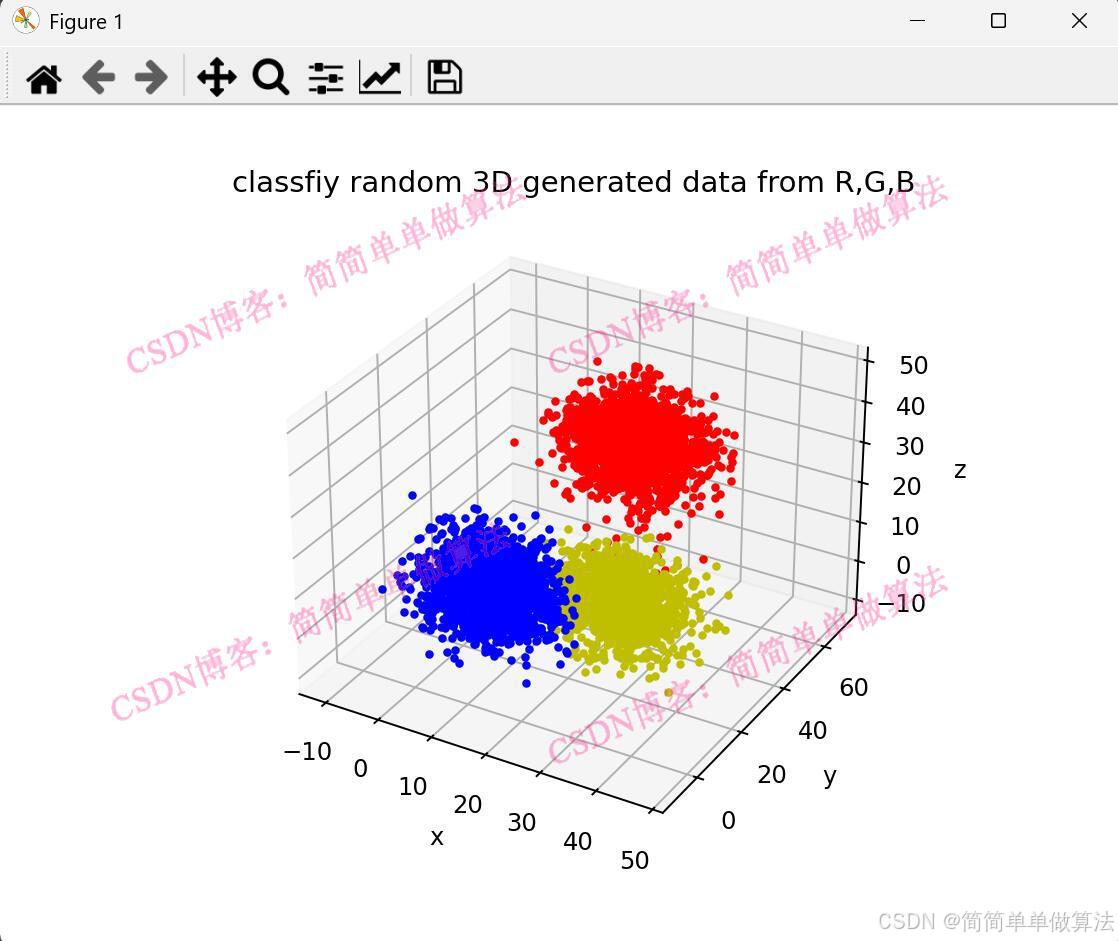
ax.scatter(X[i, 0], X[i, 1], X[i, 2],c=color[int(order[i])], s=25 ,marker='.')
plt.title('classfiy random 3D generated data from R,G,B')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show()
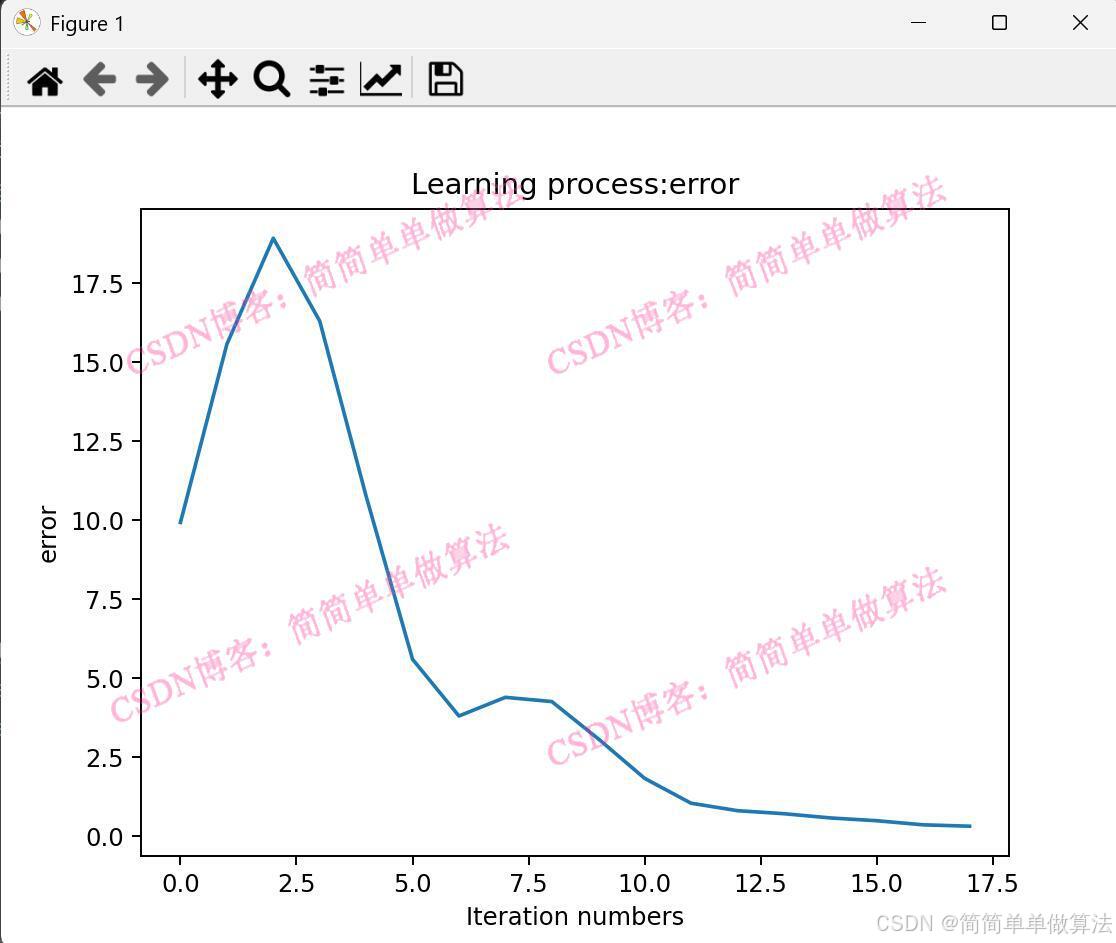
plt.plot(Learn_process[2:iter_num]);
plt.title('Learning process:error')
plt.xlabel('Iteration numbers')
plt.ylabel('error')
plt.show()
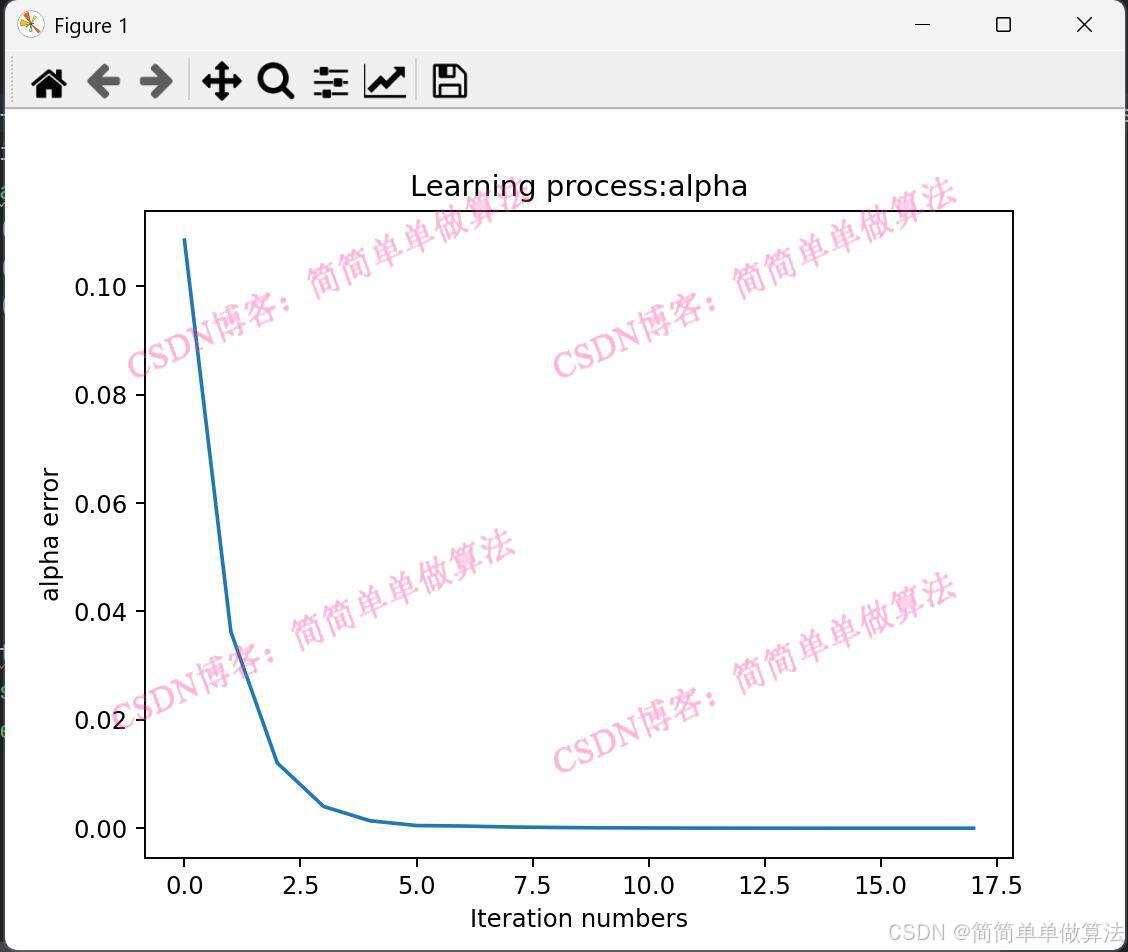
plt.plot(alpha_process[2:iter_num]);
plt.title('Learning process:alpha')
plt.xlabel('Iteration numbers')
plt.ylabel('alpha error')
plt.show()
plt.plot(cov_process[2:iter_num]);
plt.title('Learning process:cov')
plt.xlabel('Iteration numbers')
plt.ylabel('cov error')
plt.show()
4.算法理論概述
EM期望最大化算法是一種用于含有隱變量(latent variable)的概率模型參數(shù)估計的迭代算法。在許多實際問題中,數(shù)據(jù)的生成過程可能涉及一些無法直接觀測到的變量,這些變量被稱為隱變量。例如在混合高斯模型(Gaussian Mixture Model,GMM)中,每個數(shù)據(jù)點具體來自哪個高斯分布就是一個隱變量。EM算法通過交替執(zhí)行兩個步驟:E步(期望步)和M步(最大化步),逐步逼近最優(yōu)的參數(shù)估計。
4.1 EM算法

這是因為在E步中,我們計算的是在當(dāng)前參數(shù)下關(guān)于隱變量的期望,而在M步中,我們通過最大化這個期望來更新參數(shù),使得似然函數(shù)單調(diào)遞增。理論上,當(dāng)似然函數(shù)的變化小于某個閾值時,算法收斂到局部最優(yōu)解。
4.2 GMM模型
混合高斯模型(Gaussian Mixture Model,簡稱 GMM) 是一種概率模型,通過將數(shù)據(jù)視為由多個高斯分布(正態(tài)分布)的加權(quán)組合而生成,適用于聚類、密度估計、數(shù)據(jù)分布建模等場景。相比常見的 K-Means 聚類,混合高斯模型能夠捕捉到數(shù)據(jù)分布的方差差異和協(xié)方差結(jié)構(gòu)。




 浙公網(wǎng)安備 33010602011771號
浙公網(wǎng)安備 33010602011771號