基于PSO粒子群優化的BiLSTM雙向長短期記憶網絡序列預測算法matlab仿真,對比BiLSTM和LSTM
1.算法運行效果圖預覽
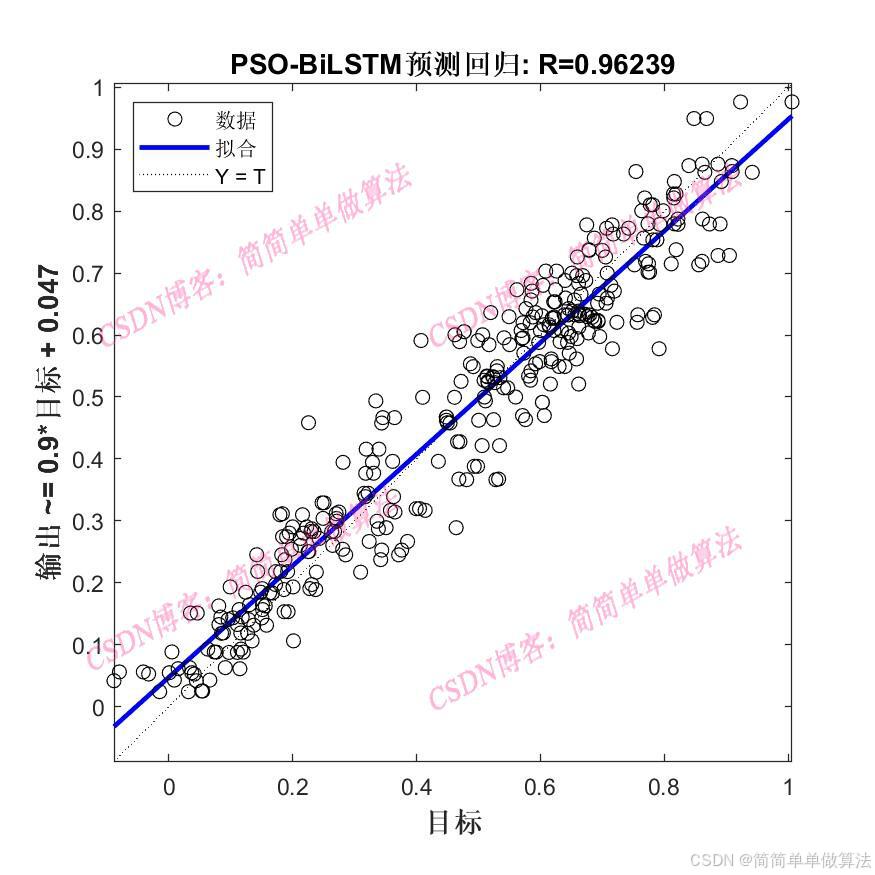
(完整程序運行后無水印)
2.算法運行軟件版本
matlab2022a/matlab2024b
3.部分核心程序
(完整版代碼包含詳細中文注釋和操作步驟視頻)
figure;
plot(gb1,'-bs',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.0,0.0]);
xlabel('優化迭代次數');
ylabel('適應度值');
figure
plot(gb1,'linewidth',2);
grid on
xlabel('迭代次數');
ylabel('遺傳算法優化過程');
legend('Average fitness');
X = g1;
%bilstm
layers=bilstm_layer(bw_in,round(X(1)),round(X(2)),bw_out,X(3),X(4),X(5));
%參數設定
opts = trainingOptions('adam', ...
'MaxEpochs',10, ...
'GradientThreshold',1,...
'ExecutionEnvironment','cpu',...
'InitialLearnRate',X(6), ...
'LearnRateSchedule','piecewise', ...
'LearnRateDropPeriod',2, ...
'LearnRateDropFactor',0.5, ...
'Shuffle','once',...
'SequenceLength',1,...
'MiniBatchSize',64,...
'Verbose',1);
%網絡訓練
[net1,INFO] = trainNetwork(Xtrain,Ytrain,layers,opts);
Rmsev = INFO.TrainingRMSE;
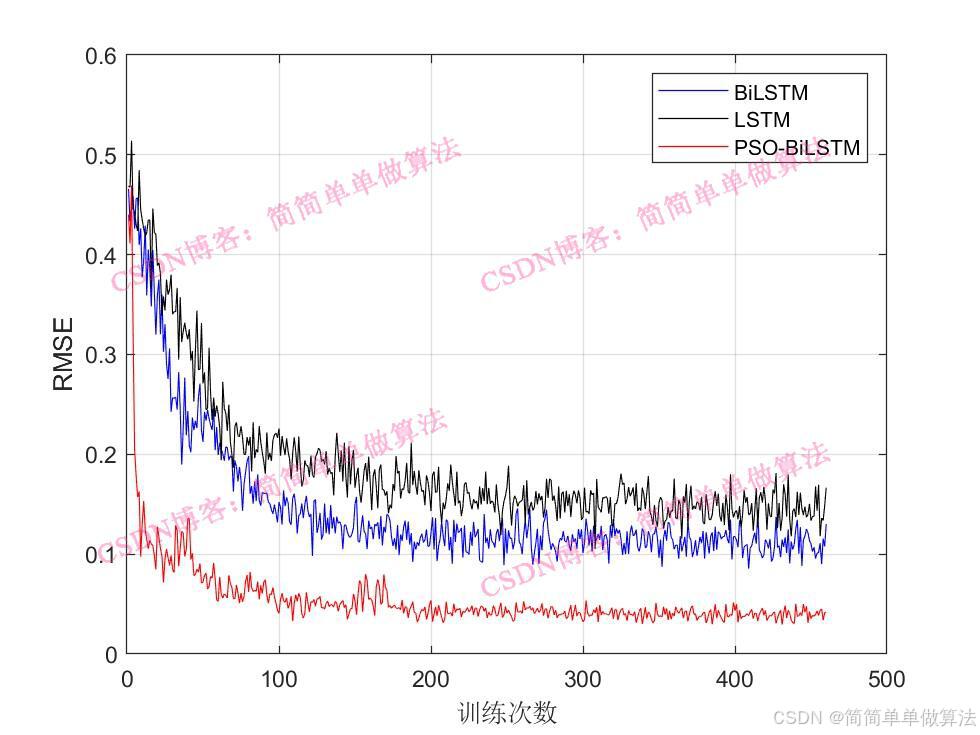
figure;
plot(Rmsev)
xlabel('訓練次數');
ylabel('RMSE');
%預測
for i = 1:length(Xtest)
Ypred(i) = net1.predict(Xtest(i));
end
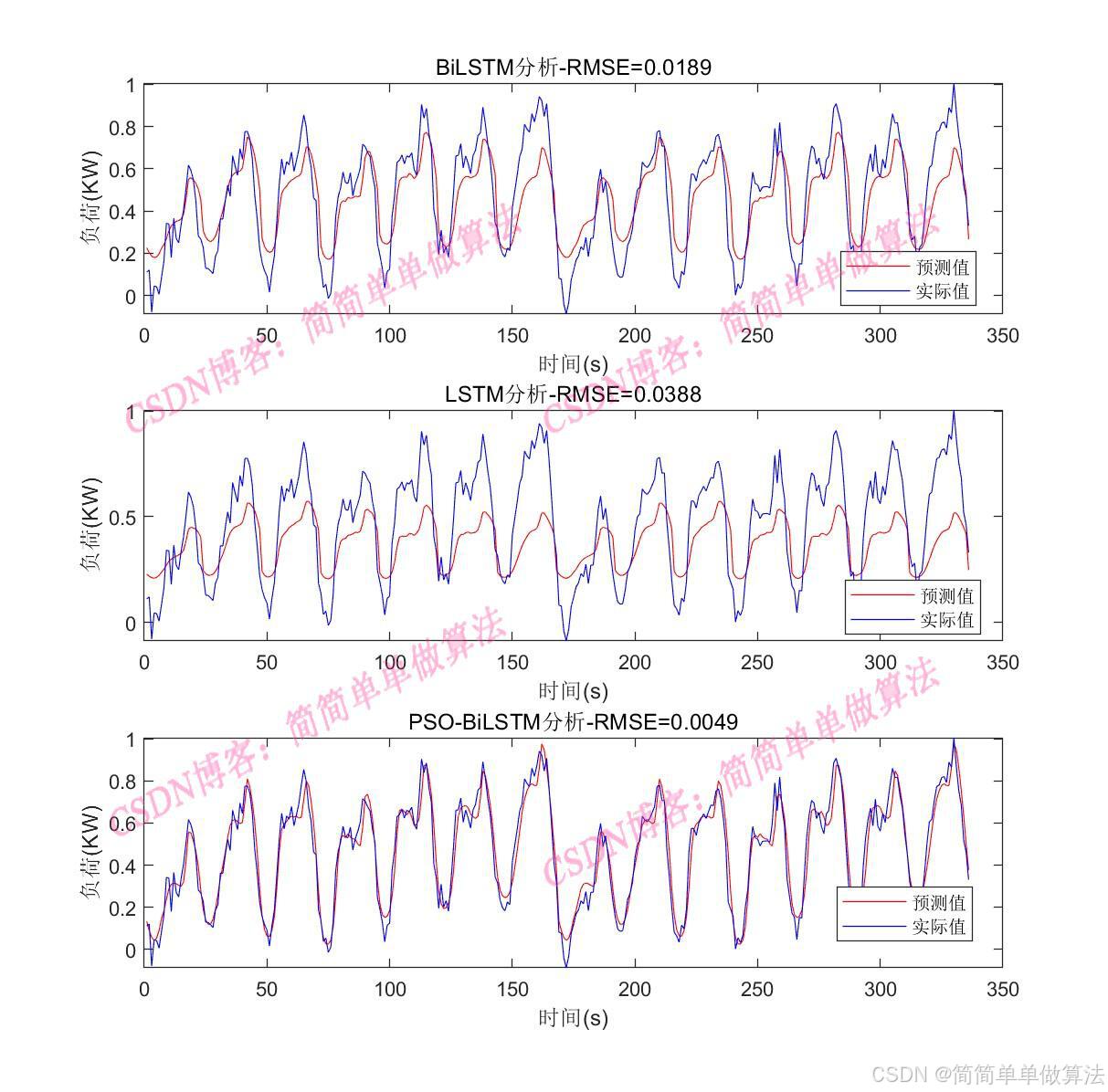
figure
plot(Ypred,'r-')
hold on
plot(Ytest','b-')
legend('預測值','實際值')
xlabel('時間(s)')
ylabel('負荷(KW)')
rmse = mean((Ypred(:)-Ytest(:)).^2);% 計算均方根誤差
title(sprintf('PSO-biLSTM分析-RMSE=%.3f', rmse));
save R3.mat Ypred Ytest rmse Rmsev
4.算法理論概述
在序列預測問題中,如氣象數據預測、交通流量預測等,準確捕捉序列中的長期依賴關系和上下文信息是關鍵。雙向長短期記憶網絡(BiLSTM)能有效處理長序列數據,同時考慮序列的過去和未來信息,但BiLSTM的性能受其參數設置的影響較大。粒子群優化算法(PSO)是一種基于群體智能的優化算法,具有全局搜索能力強、收斂速度快等優點。將PSO應用于BiLSTM的參數優化,可以提高BiLSTM的序列預測性能。
LSTM是一種特殊的循環神經網絡(RNN),旨在解決傳統 RNN 在處理長序列時的梯度消失和梯度爆炸問題,從而更好地捕捉長序列中的長期依賴關系。其核心結構包含輸入門、遺忘門、輸出門以及記憶單元。
BiLSTM 是在 LSTM 基礎上發展而來,它通過同時向前和向后處理序列,能夠更好地捕捉序列中的前后文信息,從而在序列預測任務中表現更優。BiLSTM 由一個前向 LSTM 和一個后向 LSTM 組成。

這種結構使得 BiLSTM 能夠同時利用序列的前文和后文信息,在處理需要全局信息的序列預測任務時具有明顯優勢。
在本課題中,將pso應用于BiLSTM主要是為了優化BiLSTM的超參數,如學習率、隱藏層神經元數量等,以提升其預測性能。大致的步驟如下:
1.隨機初始化一群粒子的位置和速度,每個粒子的位置對應一組 BiLSTM 的參數。
2.使用訓練集對 BiLSTM 進行訓練,并根據驗證集的預測結果定義適應度函數。常見的適應度函數是均方誤差(MSE):

PSO能夠在參數空間中進行全局搜索,有助于找到更優的BiLSTM參數組合,避免陷入局部最優解。



 浙公網安備 33010602011771號
浙公網安備 33010602011771號