證明的起源

英文：https://plus.maths.org/content/os/issue7/features/proof1/index

證明是什么？幾個世紀以來，哲學家們一直在爭論這個問題，以及如何證明(還有是否能證明！)。毫無疑問，他們會繼續這樣做！另一方面，數學家們一直在使用證明的“可操作性定義”來促進數學知識的發展。
從本期開始，Pass Maths會發表一系列文章，介紹證明和邏輯推理背后的一些基本概念，并展示它們在數學中的重要性。
在這篇文章中，我們將簡要介紹演繹推理，并看一看已知的最早的數學證明例子之一。

演繹推理

給出一組已知或假設為真的事實，演繹推理是擴展這組事實的一種強有力的方式。在演繹推理中，我們認為如果某些前提(P)是已知或假設的，那么結論(C)必然由此而來。例如，給定以下內容(相當有名！)作為前提。

P: 所有的男人都是凡人。
P: 蘇格拉底是個男人。

那么結論就是

C: 蘇格拉底是凡人。

通過演繹推理得出結論。在這種情況下，演繹步驟是基于這樣的邏輯原則：如果A推導出B，并且A是真的，那么B就是真的，這一原則被中世紀邏輯學家稱為modus ponens。
當然，演繹推理也不是萬無一失的：前提可能不是真的，或者推理路線本身可能是錯的！這就是你有時可以“證明”一些不真實的事情的方式。例如，有許多方法可以“證明”1=2。這是一句老生常談的話：

你能找出論點中的矛盾嗎？
如果一個結論不是從它的前提得出的，那么這個論點就被是無效的，無論前提是不是正確的，都不能對結論是否真實做出可靠的判斷。
如果論點是有效的，但前提不為真，那么結論可能是真的，也可能不是，但論點不能幫助我們決定這一點。
最后，如果論證有效，前提為真，那么論證過程就是合理的，我們認為結論是正確的。從實用的角度來看，如果我們能找到合理的論據，就可以說我們已經證明了一件事。
表1總結了這些不同類型的演繹論點，表2提供了每種論點的示例。

表1：不同類型的邏輯概念。

一些邏輯論證的例子

正如表2中的兩個無效例子所表明的那樣，無效條件的結論不一定是假的——它只是沒有被必要條件證明而已！

開端：歐氏幾何

歐幾里得生于公元前365年左右的埃及亞歷山大，死于公元前300年左右。除了他在亞歷山大教數學之外，人們對他的一生知之甚少。

歐幾里德寫了許多論文，但最著名的是他的《原本》，這部關于幾何學的著作已經被用作教科書超過2000年了！這些元素現在被認為是對他那個時代當前幾何知識的總結，而不是代表歐幾里德的原著。然而，它們代表了數學史上最早使用證明的方法之一。

歐幾里得在他的著作《原本》中，首先列出了23個定義，描述了點、線、平面、圓、鈍角和銳角等事物(在這里，這些定義在附錄中給出)。

歐幾里德的定義既不是正確的，也不是錯誤的：他們只是充當一種字典，解釋他將使用的各種術語的含義。然后，他提出了一組假設，其中包括是個命題。其中有五個不是特定于幾何學的，他稱它們為常見概念：

• 1. 等同于同一事物的事物也是彼此相等的。
• 2. 如果兩種對等的事物相加，則整體也相等。
• 3. 如果兩種對等的事物相減，則整體也相等。
• 4. .所有全等的事物都是相等的。
• 5. 整體大于局部。

其他五個假設都是明確的幾何假設，他稱它們為假設：

• 1. 從任何一點到任何一點都可以畫一條直線。
• 2. 可以在一條直線上連續產生一條有限直線。
• 3. 可以描述具有任意圓心和距離的圓。
• 4. 所有直角都相等。
• 5. 如果一條直線落在兩條直線上，使同一側的內角小于兩個直角，則這兩條直線如果無限期地產生，則在其角度小于兩個直角的那一邊相交。

(請注意，Playfair的公理(最初是由于Proclus)所說的“過一個不在給定線上的點，平行于這條線的線不超過一條”是表達假設5的一種相當整潔的方式！此外，在十九世紀，勒讓德繼續證明了假設5等同于“三角形的角之和等于兩個直角”的假設)。

這些共同的概念和假設共同代表了歐幾里得幾何學的基本公理。公理是一種假設為真而不是被證明的邏輯原理，可以作為演繹論證的前提。

歐幾里得的一套公理，或公理系統，代表了一組“第一原則”，從這些原則中可以使用演繹推理產生其他原則。當然，只有在歐幾里得的共同概念和假設真的成立的情況下，任何演繹論證才是合理的！

一個命題及其證明

歐幾里得在他的基本原理中提出了各種幾何命題，并在他的公理系統中使用演繹推理證明了這些命題是正確的。
命題6就是一個例子：“如果三角形中的兩個角相等，那么兩個角相交的邊長也是相等的。”
歐幾里得對這一命題的實際證明如下：

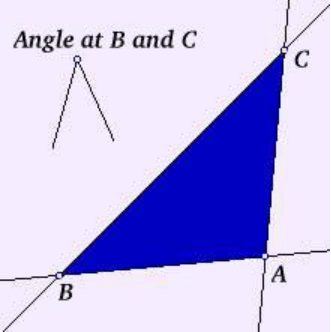
圖1：歐幾里德的命題6。，

“設三角形ABC的三個角大小分別為A，B，C；我令AB等于AC，如果他們不等，則必然有其中一個更大。我們讓AB作為其中更大的一方，讓DB等于AB中切除等于AC剩余部分的長度；最后連接DC。

之后，由于DB等于AC，并且BC是公共邊，所以邊DB、邊BC分別等于邊AC、邊CB，并且∠DBC等于∠ACB。

因此，底邊DC等于底邊AB，而三角形DBC等于三角形ACB，小三角形等于大三角形，這是荒謬的。因此，AB不等于AC的結論是荒謬的。所以由反證法，AB等于AC

如果你有一個支持Java的瀏覽器，你可以在這里嘗試一下這幅圖的動態版本。

歐幾里得的假設是真的嗎？

歐幾里得時代的希臘人和后來的阿拉伯數學家都有一種直覺，即第五個公設實際上可以用定義和常見概念以及前四個公設來證明。

人們曾多次嘗試以這種方式證明第五個假設，通常推定的證明會被接受很長一段時間，然后才會被證明是有缺陷的。通常情況下，這些有缺陷的證明包含一個“循環論證”：為了證明這一點，他們以這樣或那樣的方式假定他們試圖證明的東西(第五個假設)是真的！

事實上，第五個假設并不是完全可以從其他假設和概念中推導出來的，也不是普遍成立的。幾個世紀以來，數學家們一直對第五個公設著迷，但直到十九世紀和二十世紀(通過許多著名數學家的努力，包括勒讓德、高斯、博萊伊、羅巴切夫斯基、黎曼、貝爾特拉米和克萊因)，我們才了解到第五個公設不成立的幾何(稱為非歐幾里德幾何)。

第五個假設在平面幾何(或歐幾里得幾何)中可以證明是正確的。然而，還有許多其他幾何不是正確的。令人驚訝的是，這很容易說明！考慮球面的簡單情況。

在球面上畫一條真正的直線是不可能的，所以在球面幾何中，直線的歐幾里得思想變成了一個大圓。想想地球，任何一條經線都是一個大圓——赤道也是如此。事實上，球面上任意兩點之間的最短路徑是一個大圓。(更一般地，任何曲面上的最小路徑稱為測地線。)。

歐幾里得的前四個假設的結果之一是，如果兩條不同的線相交，它們會在一個點相交。這給球體帶來了一個小問題，因為截然不同的大圓圈總是在兩個對腳點相交！北極和南極的兩條經線總是相交的！

但請記住，我們還沒有說過歐幾里得點的近似球面是什么！我們所要做的就是將球面幾何中的一個點定義為一對對角點，問題很快就會消失。

根據歐幾里得第23號的定義，“平行直線是在同一平面上，在兩個方向上無限期地產生，在任何一個方向上都不相交的直線”。

根據這些定義，很容易看出歐幾里得的前四個假設仍然很有意義。然而，第五個假設失敗了，因為不可能畫出兩條不相交的不同線。在球面幾何學中，幾乎沒有平行線！

第五個假設失敗的后果之一是，三角形的角的和總是180度的說法不再正確。

事實上，有一個著名的橫向思維難題，它隱含地依賴于這個非歐幾里得幾何學：

一天早晨，一個獵人離開家，向南走了一英里。然后，他向西走了一英里，射殺了一只熊，然后向北走了一英里，回到了他家。

熊是什么顏色的?

歐幾里得與演繹推理

歐幾里得幾何的故事，以及隨后非歐幾里得幾何的發現，顯示了使用公理演繹推理作為證明系統的優點和缺點。

歐幾里得把他的定義、普通概念和公設作為一個公理系統，能夠給出一些重要幾何命題的演繹證明。他的公理和證明對后來的許多數學家來說是一套有用的工具，并展示了演繹推理是多么強大和有益！

然而，發現非歐幾里得幾何的漫長而痛苦的過程顯示了公理系統中演繹推理的局限性之一：任何證明都取決于它開始的公理！在歐幾里得平面上，歐幾里得的第五個假設是正確的，他的有效證明是可靠的。然而，在非歐幾里得幾何中，例如球面，第五個假設并不完全正確，因此歐幾里得的證明是不可靠的。