【Ray Tracing The Next Week 超詳解】 光線追蹤2-7 任意長方體 && 場景案例
上一篇比較簡單,很久才發是因為做了一些好玩的場景,后來發現這一章是專門寫場景例子的,所以就安排到了這一篇
Preface
這一篇要介紹的內容有:
1. 自己做的光照例子
2. Cornell box畫質問題及優化方案
3. 新的場景幾何體——長方體
軸平行長方體
任意長方體
我們這一篇重實踐輕理論闡述
ready
1. 需要上一章的知識
但是,上一章的Cornell box畫質優化僅限于盒子本身,如果作為場景和其他物體放在一起就不能那么優化畫質
即,Cornell box像素計算失敗應該返回黑色點而非白色
2. 需要圖形學基本仿射變換知識
3. 玻璃球鏤空技術,如有忘記,請移步此處
先看效果
光照案例
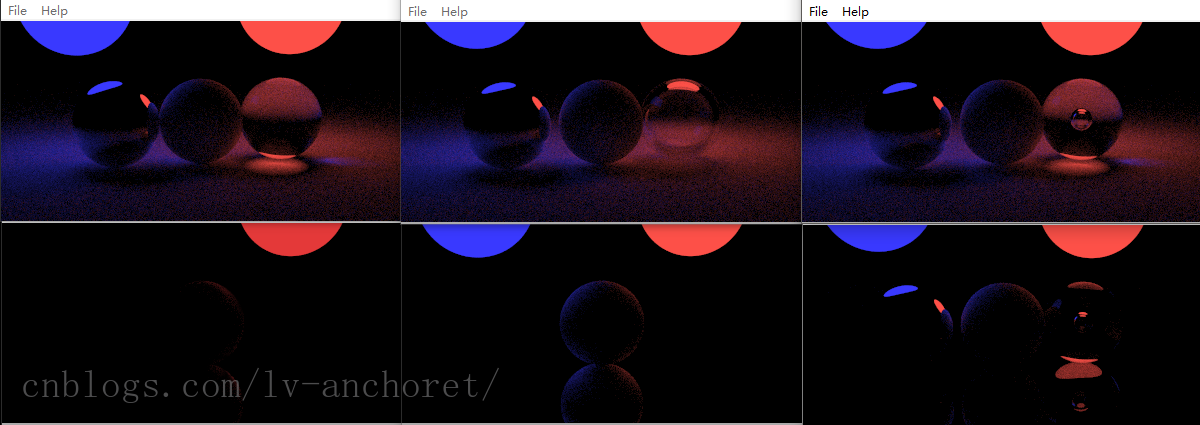
圖7-1

Cornell box案例(最初步)

圖7-2
最終版

任意軸旋轉
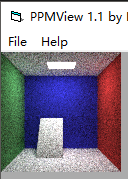

正文
學了光照就迫不及待地整了一堆東西
終于脫開了藍色插值背景轉到正兒八經的光了
在還沒學長方形之前,就先用球體做了光源
注:坐標軸按照光線追蹤坐標系描述(y軸位于垂直向上方向,z軸垂直屏幕向外)
1. 圖7-1 第二行左
該圖是最開始的一張圖,相機仍然在(13,3,2),第一卦限
而球體是一個半徑為1的漫反射白球,置于原點處
下面仍然是一個大的鏡面球(metal),y軸-1000處,半徑999,正好和小球相切
紅色燈光則置于第三卦限,例如:(-3,3,-3)
整個場景的背景為黑色,即光線路徑計算失敗后返回黑色
如上,則會看到球體表面有一抹紅色的色澤,然后大球鏡面反射也有一部分
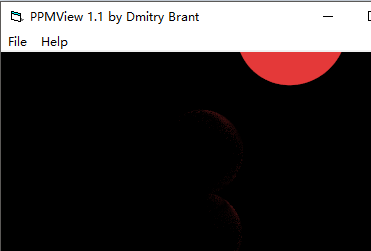
圖7-3
2. 圖7-1 第二行中
在上圖的基礎上添加一個位于第四卦限的藍色光源
就會形成漫反射球左側為藍色表面光澤右側為紅色表面光澤的效果
3. 圖7-1 第一行左
上面兩個當然很沒意思了,但是一直以來都是藍色背景亮堂堂的,第一次黑不溜秋的地方用燈照著東西,感覺挺真實的,光線追蹤效果也很不錯,所以上面兩張圖是新世紀的開端!
我們在(0,0,2)處,放一個半徑為1的鏡面球,在原點對稱處放一個半徑為1的玻璃球
下面的大球改為漫反射
哇,想想就刺激,結果不出所料
鏡面球在黑乎乎的環境下只映出了藍色光源和紅色光源,以及旁邊的漫反射球的相關部分,而玻璃球就更有意思了,透了紅光照在漫反射大球表面上,還透了微弱的藍光,也照在了右側的地面上
4. 圖7-1 第一行中
突然想到一個絕妙的主意,玻璃球可以鏤空
于是設置了一個鏤空球(0,0,-2),半徑為-0.8
之后,想著把鏡面球和磨砂小球離遠一點,再觀察磨砂小球在鏡面球中的影,于是乎就成了上面這張圖
鏡面球依舊映這磨砂小球和燈光的影,然而玻璃球只有上面一絲絲的明亮,著實看著不盡人意
可能是鏤空的太多了,于是有了右邊那張圖
5. 圖7-1 第一行右
把鏤空球半徑設置小一點,想了想就-0.2吧
果然,不負吾望,還真是著實好看,不僅可以往地上透光,形狀更有意思,像個立體環!!
其實,我是想調一個把左邊兩個特點合二為一的圖,即既有第一張圖的底面透光,又有第二圖上表面那個明亮的高光
6. 圖7-1 第二行右
其實是為了湊齊6張圖,思來想去,沒啥整的了,老是調個鏤空半徑沒啥意思,渲染時間還長,后來想了下,不如把大球改成原來的鏡面,這樣下面三張圖都是鏡子大地,上面三張都是磨砂大地
于是乎,emmm,貌似還完成了上面提到的夢想,上表面”高光”以及底面的透光,不僅如此,而且鏤空內表面還有透光,還映在了大地上,強無敵嘞~
上述場景代碼
intersect* light() { texture * perlintex = new noise_texture(6.3); material* redlight = new areaLight(new constant_texture(rtvec(0.98, 0.1, 0.08))); material* bluelight = new areaLight(new constant_texture(rtvec(0.05, 0.05, 1.))); intersect**list = new intersect*[7]; list[0] = new sphere(rtvec(-2, 3, -3), 1.5, redlight); list[1] = new sphere(rtvec(-2.2, 3.2, 2.8), 1.5, bluelight); list[2] = new sphere(rtvec(0, 0, 2.2), 1, new metal(new constant_texture(rtvec(1, 1, 1)))); list[3] = new sphere(rtvec(), 1, new lambertian(new constant_texture(rtvec(1, 1, 1)))); list[4] = new sphere(rtvec(0, 0, -2), 1, new dielectric(1.5)); list[5] = new sphere(rtvec(0, 0, -2), -0.18, new dielectric(1.5)); list[6] = new sphere(rtvec(0, -1000, 0), 999, new dielectric(1.5)); return new intersections(list, 7); }
Chapter 7:Instance
我們來進行正常的章節學習,emmmm
現在先來學習軸平行的長方體,這個東西呢我知道的目前有兩種方法
第一種是球坐標系下多個方位角和長寬高參數確定的長方體
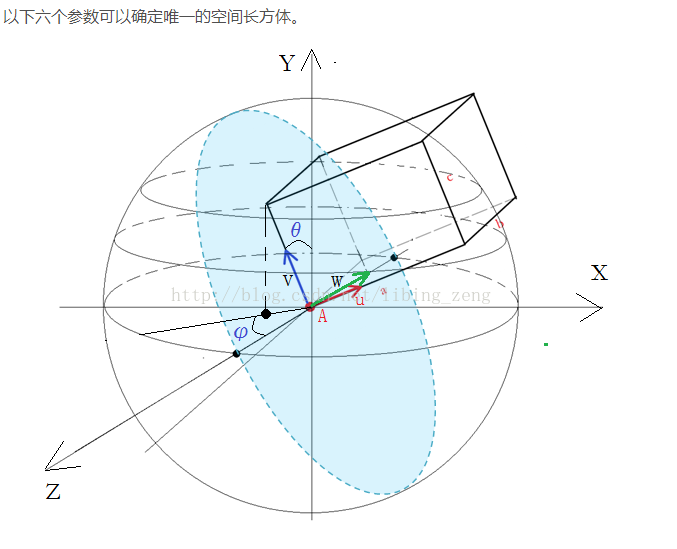
此圖引用于https://blog.csdn.net/libing_zeng/article/details/54561605
如果想要學習的話可以去學習一下這種方法
第二種方法自然就是頂點確定形體,左下-右上頂點確定形體,不僅適用于2D的形,同樣適用于3D的體
心里羅列一下我們現有的零件,是否能夠整一個長方體出來,好像可以
我們已經弄好了長方形,那么就可以粘成長方體
不錯,只要把各個長方形的法線指向外部即可,而第一種方法也要求取每個面的法線
所以,我們這種方法還是比較好的,畢竟我們就是用6個法線構建的,第一種還需要方位角轉換運算求取
那么我們就寫成了如下代碼
/// box.hpp // ----------------------------------------------------- // [author] lv // [begin ] 2019.1 // [brief ] the box-class for the ray-tracing project // from the 《ray tracing the next week》 // ----------------------------------------------------- #pragma once namespace rt { // the statement of box class class box: public intersect { public: box() { } box(const rtvec& pointmin, const rtvec& pointmax, material * mat); virtual bool hit(const ray& sight, rtvar t_min, rtvar t_max, hitInfo& info)const override; virtual aabb getbox()const override; private: rtvec _min; rtvec _max; intersect* _list; }; // the implementation of box class inline box::box(const rtvec& pointmin, const rtvec& pointmax, material * mat) :_min(pointmin) ,_max(pointmax) { intersect ** list = new intersect*[6]; list[0] = new xy_rect(_min.x(), _max.x(), _min.y(), _max.y(), _max.z(), mat); list[1] = new flip_normal(new xy_rect(_min.x(), _max.x(), _min.y(), _max.y(), _min.z(), mat)); list[2] = new xz_rect(_min.x(), _max.x(), _min.z(), _max.z(), _max.y(), mat); list[3] = new flip_normal(new xz_rect(_min.x(), _max.x(), _min.z(), _max.z(), _min.y(), mat)); list[4] = new yz_rect(_min.y(), _max.y(), _min.z(), _max.z(), _max.x(), mat); list[5] = new flip_normal(new yz_rect(_min.y(), _max.y(), _min.z(), _max.z(), _min.x(), mat)); _list = new intersections(list, 6); } bool box::hit(const ray& sight, rtvar t_min, rtvar t_max, hitInfo& info)const { return _list->hit(sight, t_min, t_max, info); } aabb box::getbox()const { return aabb(_min, _max); } } // rt namespace
根據最小點坐標和最大點坐標構建六個面
于是我們來做開篇第二張圖

在上一篇文章的Cornell box的場景中添加上面兩個box
如果你的代碼中,上一篇的仍然是背景為白色(即光線路徑計算失敗后返回白色)
那么將是下面這個
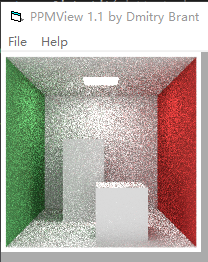
圖7-4
面向我們的兩個物體面是光線追蹤幾乎計算不到的地方,所以基本是純白色
我們迫不得已再把背景改為黑色

如第34行所示
但是我們一想到上一篇的一堆黑點噪聲就。。。真是把一張美圖糟蹋了

圖7-5
如何優化呢?
思來想去,有下列幾種方法
1. 把區域光面積調大
2. 把光源與頂部距離調大,因為房間的每一面墻壁都是邊長為555的正方形,敢問,距離為一個像素的光如何把偌大的平面照亮,于是乎,我改成了距離5....
3. 相機距離房間門口800像素,我們調為700像素
則修改后的圖像為:
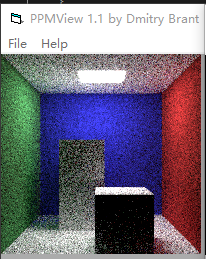
圖7-6
還有一個最重要的改進方式,增加采樣點,即增加光線條數
可以對比,sample為10的時候(之前是sample為100)
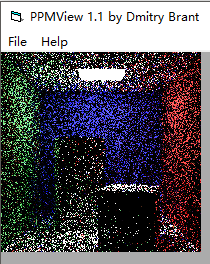
圖7-7
從《Ray Tracing From the Ground Up》中得知,最簡單粗暴的方法是發出萬條光線做路徑計算可以得到我們想要的圖片
于是我將sample改為了2w,跑了一夜,現在是這樣的

圖7-8
可以看出來是相當清晰了
書中還提到了,對光線路徑和光源本身同時進行采樣計算的直接光照和間接光照結合方法優化畫質,比上述的暴力法效率更好
但是目前不會對光源進行采樣計算以及間接光照相關技術,所以不能為大家提供代碼和效果
好了,我們繼續章節學習——旋轉和平移
我們知道,平移比較簡單,但是在光線追蹤中如何實現物體平移呢?
它并沒有頂點集合,它只有一個幾何體方程以及碰撞檢測,怎么平移呢
對了,就是碰撞檢測這里!
我們對每一個碰撞點進行變換計算,也就把整個理想化的物體實例化且做了變換
1. 平移
對于平移,我們可以對每個碰撞點進行移動也可以在計算碰撞點的時候把eye往反方向移動,進而,求取碰撞點,也可以實現平移
我們采取第二種
/// translate.hpp // ----------------------------------------------------- // [author] lv // [begin ] 2019.1 // [brief ] the translate-class for the ray-tracing project // from the 《ray tracing the next week》 // ----------------------------------------------------- #pragma once namespace rt { class translate :public intersect { public: translate(intersect* p, const rtvec& offset); virtual bool hit(const ray& sight, rtvar t_min, rtvar t_max, hitInfo& info)const override; virtual aabb getbox()const override; private: intersect* _item; rtvec _offset; }; translate::translate(intersect* p, const rtvec& offset) :_item(p) , _offset(offset) { } bool translate::hit(const ray& sight, rtvar t_min, rtvar t_max, hitInfo& info)const { ray movedRay(sight.origin() - _offset, sight.direction(), sight.time()); if (_item->hit(movedRay, t_min, t_max, info)) { info._p += _offset; return true; } return false; } aabb translate::getbox()const { aabb box = _item->getbox(); return aabb(box.min() + _offset, box.max() + _offset); } }// rt namespace
這個比較簡單
2. 旋轉
我們來復習一下圖形學中仿射變換的知識
關于旋轉:(引用書上一張圖)
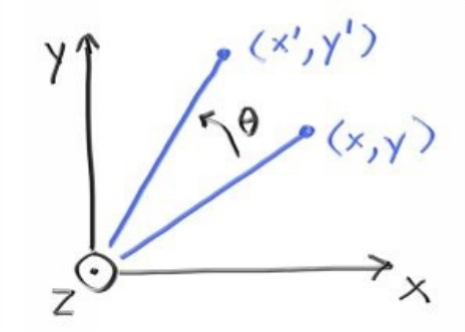
則
x' = cosθ * x - sinθ * y y' = sinθ * x + cosθ * y
那么寫成慣用的矩陣形式(采用列向量表示法),則是(繞z軸轉)
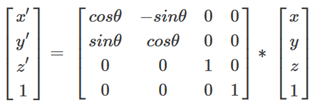
同理,繞y軸轉:
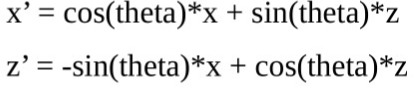
繞x軸轉:
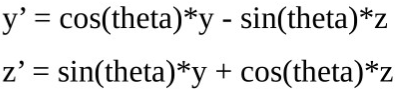
那么,我們來寫繞y軸轉的類
/// rotate.hpp // ----------------------------------------------------- // [author] lv // [begin ] 2019.1 // [brief ] the rotate-class for the ray-tracing project // from the 《ray tracing the next week》 // ----------------------------------------------------- #pragma once namespace rt { // the statement of rotate class class rotate :public intersect { public: rotate(intersect* p, rtvar angle); virtual bool hit(const ray& sight, rtvar t_min, rtvar t_max, hitInfo& info)const override; virtual aabb getbox()const override; private: intersect* _item; rtvar _sinθ; rtvar _cosθ; aabb _box; }; // the implementation of rotate class rotate::rotate(intersect* p, rtvar angle) :_item(p) { rtvar radians = (π / 180.) * angle; _sinθ = sin(radians); _cosθ = cos(radians); rtvec min(rtInf(), rtInf(), rtInf()); rtvec max = -min; for (int i = 0; i < 2; ++i) for (int j = 0; j < 2; ++j) for (int k = 0; k < 2; ++k) { rtvar x = i * _box.max().x() + (1 - i)*_box.min().x(); rtvar y = j * _box.max().y() + (1 - j)*_box.min().y(); rtvar z = k * _box.max().z() + (1 - k)*_box.min().z(); rtvar newx = _cosθ * x + _sinθ * z; rtvar newz = -_sinθ * x + _cosθ * z; rtvec tester(newx, y, newz); for (int c = 0; c < 3; ++c) { if (tester[c] > max[c]) max[c] = tester[c]; if (tester[c] < min[c]) min[c] = tester[c]; } } _box = aabb(min, max); } bool rotate::hit(const ray& sight, rtvar t_min, rtvar t_max, hitInfo& info)const { rtvec eye = sight.origin(); rtvec direction = sight.direction(); eye[0] = _cosθ * sight.origin()[0] - _sinθ * sight.origin()[2]; eye[2] = _sinθ * sight.origin()[0] + _cosθ * sight.origin()[2]; direction[0] = _cosθ * sight.direction()[0] - _sinθ * sight.direction()[2]; direction[2] = _sinθ * sight.direction()[0] + _cosθ * sight.direction()[2]; ray rotatedRay(eye, direction, sight.time()); if (_item->hit(rotatedRay, t_min, t_max, info)) { rtvec p = info._p; rtvec n = info._n; p[0] = _cosθ * info._p[0] + _sinθ * info._p[2]; p[2] = -_sinθ * info._p[0] + _cosθ * info._p[2]; n[0] = _cosθ * info._n[0] + _sinθ * info._n[2]; n[2] = -_sinθ * info._n[0] + _cosθ * info._n[2]; info._p = p; info._n = n; return true; } return false; } aabb rotate::getbox()const { return _box; } } // rt namespace
我們來寫圖7-7的場景
intersect* Cornell() { intersect ** list = new intersect*[9]; size_t cnt = 0; material * red = new lambertian(new constant_texture(rtvec(0.65, 0.05, 0.05))); material * blue = new lambertian(new constant_texture(rtvec(0.05, 0.05, 0.73))); material * white = new lambertian(new constant_texture(rtvec(0.88, 0.88, 0.88))); material * green = new lambertian(new constant_texture(rtvec(0.12, 0.45, 0.15))); material * light = new areaLight(new constant_texture(rtvec(20, 20, 20))); list[cnt++] = new flip_normal(new yz_rect(0, 555, 0, 555, 555, green)); list[cnt++] = new yz_rect(0, 555, 0, 555, 0, red); list[cnt++] = new xz_rect(200, 350, 220, 340, 550, light); list[cnt++] = new flip_normal(new xz_rect(200, 350, 220, 340, 550, light)); list[cnt++] = new flip_normal(new xz_rect(0, 555, 0, 555, 555, white)); list[cnt++] = new xz_rect(0, 555, 0, 555, 0, white); list[cnt++] = new flip_normal(new xy_rect(0, 555, 0, 555, 555, blue)); list[cnt++] = new translate(new rotate(new box(rtvec(), rtvec(165, 165, 165), white), -18), rtvec(130, 0, 65)); list[cnt++] = new translate(new rotate(new box(rtvec(), rtvec(165, 330, 165), white), 15), rtvec(265, 0, 295)); return new intersections(list, cnt); }
圖7-8是圖7-7的高清版,暫時還沒跑完,渲染完之后我在此處放上此場景的高清版,以及任意軸旋轉的擴充代碼
敬請期待。。。
**************************** 更新線 ******************************************
圖7-8已經更新,程序終于跑完了
一張圖片分了四部分一起跑還跑了兩天,心累。。
感覺計算機也累,心疼1s
關于任意軸旋轉
上述說明了y軸旋轉的代碼
旋轉類中有三處需要做變換,向量運算也好,矩陣運算也罷
第一處是構造函數中的newx和newz(對稱軸剩余兩個分量)
第二處是hit函數中的eye運算和direction運算
第三處是hit函數中的p和n向量的運算
其中第一處和第三處用的是變換矩陣的原形(你可以先把上面的三個軸對應變換表達式轉化為矩陣形式,如第一個的z軸旋轉公式)
而第二處用的是對應變換矩陣的轉置
如此續寫其他兩個軸的旋轉類即可達成效果
當然你也可以寫個場景測試一下
至于空間任意變換,無疑就是軸旋轉和平移搭配結合所形成的效果
可以先在原點處構建物體,經多個軸旋轉而后平移到目標位置以代替空間物體沿任意軸旋轉的效果
場景測試代碼
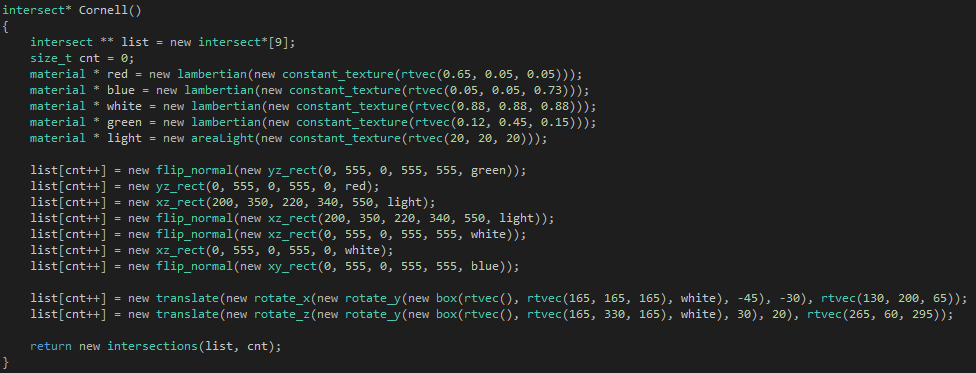

我們來對比一下各種采樣數的效果對比
sample為100

sample為500
sample為1000(該場景為下一章的體積煙霧)

sample為20000

感謝您的閱讀,生活愉快~


 浙公網安備 33010602011771號
浙公網安備 33010602011771號