給定一個(gè)n個(gè)點(diǎn)m條邊的有向圖,圖中可能存在重邊和自環(huán),所有邊權(quán)均為正值。
請(qǐng)你求出1號(hào)點(diǎn)到n號(hào)點(diǎn)的最短距離,如果無(wú)法從1號(hào)點(diǎn)走到n號(hào)點(diǎn),則輸出-1。
輸入格式
第一行包含整數(shù)n和m。
接下來(lái)m行每行包含三個(gè)整數(shù)x,y,z,表示存在一條從點(diǎn)x到點(diǎn)y的有向邊,邊長(zhǎng)為z。
輸出格式
輸出一個(gè)整數(shù),表示1號(hào)點(diǎn)到n號(hào)點(diǎn)的最短距離。
如果路徑不存在,則輸出-1。
數(shù)據(jù)范圍
1≤n,m≤1051≤n,m≤105,
圖中涉及邊長(zhǎng)均不超過(guò)10000。
輸入樣例:
3 3
1 2 2
2 3 1
1 3 4
輸出樣例:
3
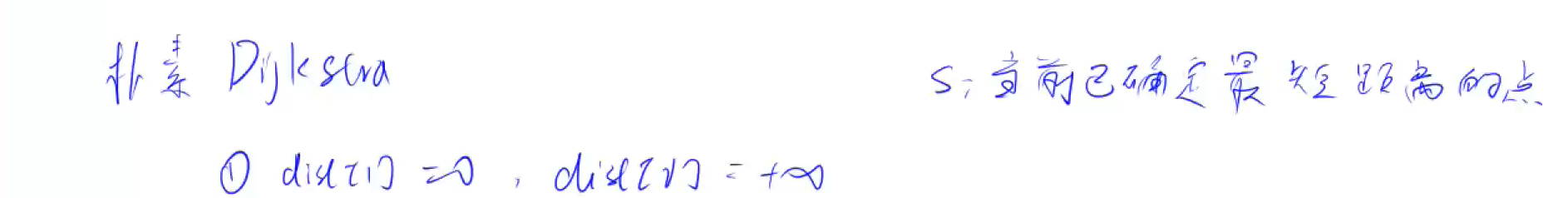

代碼實(shí)現(xiàn):
//堆優(yōu)化版本的dijkstra()
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
//我們需要用堆來(lái)維護(hù)所有的點(diǎn)的距離,維護(hù)距離的時(shí)候我們需要知道結(jié)點(diǎn)編號(hào)是多少
//所以堆里邊存的其實(shí)是一個(gè)pair
typedef pair<int,int> PII;
const int N = 1e5 + 10;
//n,m都是1e5,屬于稀疏圖用鄰接表
int d[N];
int h[N],ne[N],e[N],idx;
bool st[N];
//權(quán)重
int w[N];
int n,m;
void add(int a,int b,int c){
e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx ++;
}
int dijkstra(){
memset(d,0x3f,sizeof d);
d[1] = 0;
//小根堆
priority_queue<PII,vector<PII>,greater<PII>> heap;
//首先先把1號(hào)點(diǎn)放上去,因?yàn)?號(hào)點(diǎn)已經(jīng)知道是最短距離了
//所以先把1號(hào)點(diǎn)放上去跟新所有的點(diǎn)
heap.push({0,1});//距離是0編號(hào)是1
//當(dāng)隊(duì)列不為空
while(heap.size()){
//每次找到堆里邊距離最小的點(diǎn),也就是找到堆的起點(diǎn)
auto t = heap.top();
heap.pop();
//用ver來(lái)表示結(jié)點(diǎn)的編號(hào),用distance來(lái)表示結(jié)點(diǎn)的距離
int ver = t.second,distance = t.first;
//如果ver這個(gè)結(jié)點(diǎn)之前已經(jīng)出來(lái)過(guò)了,說(shuō)明當(dāng)前這個(gè)點(diǎn)是一個(gè)冗余備份
//所以沒(méi)有必要再處理它了,直接continue就完事了
if(st[ver]) continue;
st[ver] = true;
//后面就用當(dāng)前這個(gè)點(diǎn)更新這個(gè)點(diǎn)就完事了
//更新的話就遍歷一下所有的鄰邊
for(int i = h[ver];i != -1;i=ne[i]){
//用j存儲(chǔ)該結(jié)點(diǎn)的編號(hào)
int j = e[i];
//更新
//如果當(dāng)前距離d[j]大于從t過(guò)來(lái)的距離的話,就把d[j]更新下
if(d[j] > distance + w[i]){
//更新較小的距離
d[j] = distance + w[i];
//再將j這個(gè)點(diǎn)放在優(yōu)先隊(duì)列里邊去
heap.push({d[j],j});
}
}
}
if(d[n] == 0x3f3f3f3f) return -1;
return d[n];
}
int main(){
cin >> n >> m;
//鄰接表初始化表頭
memset(h,-1,sizeof h);
while(m --){
int x,y,z;
cin >> x >> y >> z;
add(x,y,z);
}
//用鄰接表不用去除重邊,因?yàn)樗惴ū旧肀WC了最短路,所以不需要對(duì)重邊做特殊的處理
cout << dijkstra() << endl;
return 0;
}



 浙公網(wǎng)安備 33010602011771號(hào)
浙公網(wǎng)安備 33010602011771號(hào)