狀態空間模型 (SSM)

狀態空間模型（SSM），與Transformer和RNN一樣，用于處理信息序列，例如文本和信號。

SSM 是用于描述這些狀態表示并根據某些輸入預測其下一個狀態可能是什么的模型,然而，它不使用離散序列，而是將連續序列作為輸入并預測輸出序列

 

 

1.什么是狀態空間？

狀態空間是一組能夠完整捕捉系統行為的最少變量集合。它是一種數學建模方法，通過定義系統的所有可能狀態來表述問題。

 在語言模型中，我們經常使用嵌入或向量來描述輸入序列的“狀態”。

 在神經網絡的語境中，“狀態”通常指的是網絡的隱藏狀態。在大型語言模型的背景下，隱藏狀態是生成新tokens的一個關鍵要素。

2.SSM公式來源

參考：https://www.bilibili.com/video/BV1n7421d7xG/?spm_id_from=333.337.search-card.all.click&vd_source=8e62d7fcd6fc4f51e61f64cd117a89c2

3.離散SSM和連續SSM對比

 4.離散化

 零階保持技術：

 推導過程：

5.什么是狀態空間模型？

狀態空間模型（SSM）是用來描述這些狀態表示，并根據給定的輸入預測下一個可能狀態的模型。

SSM是控制理論中常用的模型，在卡爾曼濾波、隱馬爾可夫模型都有應用。它是利用了一個中間的狀態變量，使得其他變量都與狀態變量和輸入線性相關，極大的簡化問題。

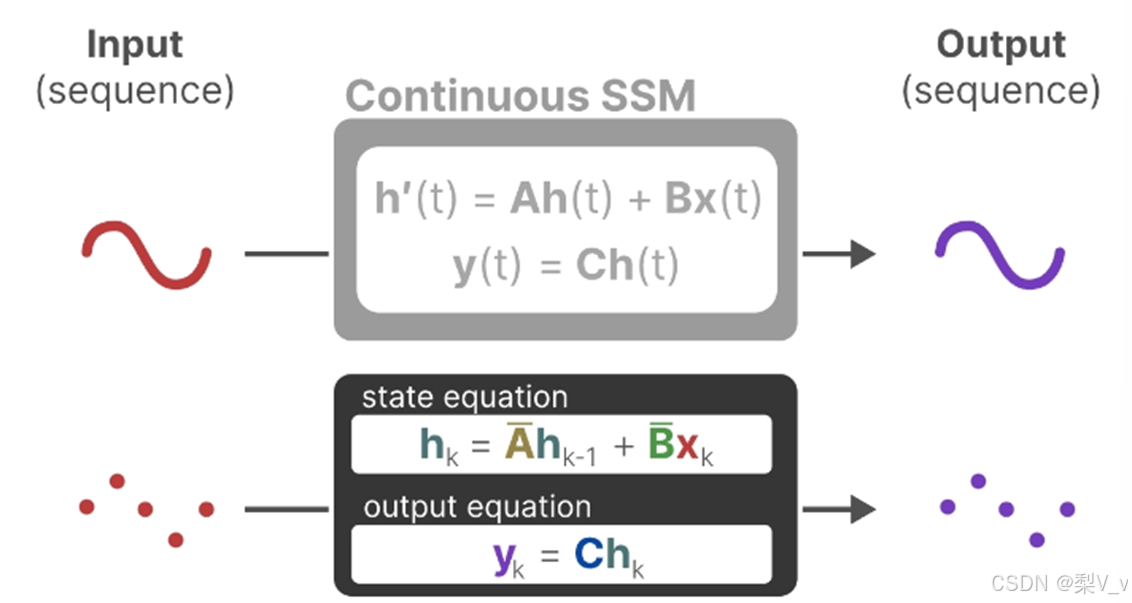
狀態空間模型（SSM）假定動態系統（比如在三維空間中移動的物體）的狀態可以通過兩個數學方程來預測，這兩個方程描述了系統在時間t時的狀態如何隨時間演變。

 這兩個方程構成了狀態空間模型的核心。

A是存儲著之前所有歷史信息的濃縮精華(可以通過一系列系數組成的矩陣表示之)，以基于A更新下一個時刻的空間狀態hidden state

注：“這里就是導數，是SSM 一階微分方程 中的導數，這里還是連續型，不是離散型，畢竟只有在離散系統中才是t和t-1” 

總之，通過求解這些方程，可以根據觀察到的數據：輸入序列和先前狀態，去預測系統的未來狀態

SSM的關鍵是找到：狀態表示(state representation)—— ，;以便結合「其與輸入序列」預測輸出序列；而這兩個方程也是狀態空間模型的核心( 一方面 ， A、B、C、D這4個矩陣是參數，是可以學習到的，二方面，學習好之后，在SSM中，矩陣A、B、C、D便固定不變了——即便是在不同的輸入之下，但到了后續的改進版本mamba中則這4個矩陣可以隨著輸入不同而可變)

第一個方程：狀態方程，

連續時間：用微分方程描述，對時間的導數。

離散時間：用差分方程描述，h(t-1)表示上一時刻狀態。

狀態方程展示了輸入如何通過矩陣B影響狀態，以及狀態如何通過矩陣A隨時間變化。

 h(t)指的是任何給定時間t的潛在狀態表示，而x(t)指的是某個輸入。

第二個方程：輸出方程，描述了狀態如何轉換為輸出(通過矩陣 )，

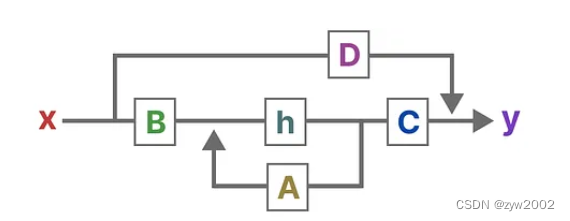
設想我們有一個輸入信號x(t)，這個信號首先與矩陣B相乘，而矩陣B刻畫了輸入對系統的影響程度。更新后的狀態（類似于神經網絡的隱藏狀態）是一個潛在空間，它包含了環境的核心“知識”。我們將這個狀態與矩陣A相乘，矩陣A揭示了所有內部狀態是如何相互連接的，因為它們代表了系統的基本動態。矩陣A在創建狀態表示之前被應用，并在狀態表示更新之后進行更新。利用矩陣C來定義狀態如何轉換為輸出。</p><p>我們可以利用矩陣 D提供從輸入到輸出的直接信號。這通常也稱為跳躍連接。

由于矩陣 D類似于跳躍連接，因此在沒有跳躍連接的情況下，SSM 通常被視為如下,SSM通常被認為是不包含跳躍連接的部分。

 

簡化視角

6.舉例-離散SSM

7.時不變特性

之所以叫時不變（與時間無關），就是 ABCD參數是固定的，這當然是一種假設，而且是個強假設。D在許多實際系統中，它可以是零。很多人學 SSM漸漸就忘了這個強假設。Transformer本身是沒有這樣的假設的，也就是說可以用于時變系統和非線性系統。

犧牲通用性，換來特定場景下的更高性能，這就是所有SSM模型的最底層邏輯。

離散化：離散化主要是為了方便計算機處理。

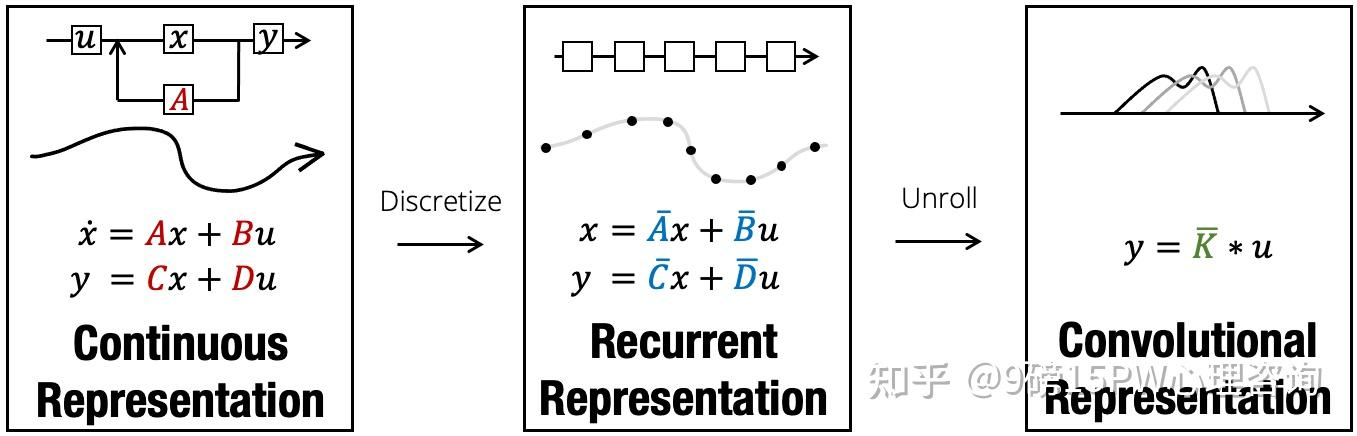
在實際應用SSM時，離散化是其核心思想。該架構的所有便利性都在于這一步，因為它使我們能夠從SSM的連續視角傳遞到另外兩個：遞歸視角以及卷積視角

 

 

 

s4模型-structured state spaces for sequences

1.從SSM中獲得啟發，提出S4模型，將SSM引入深度學習領域

 

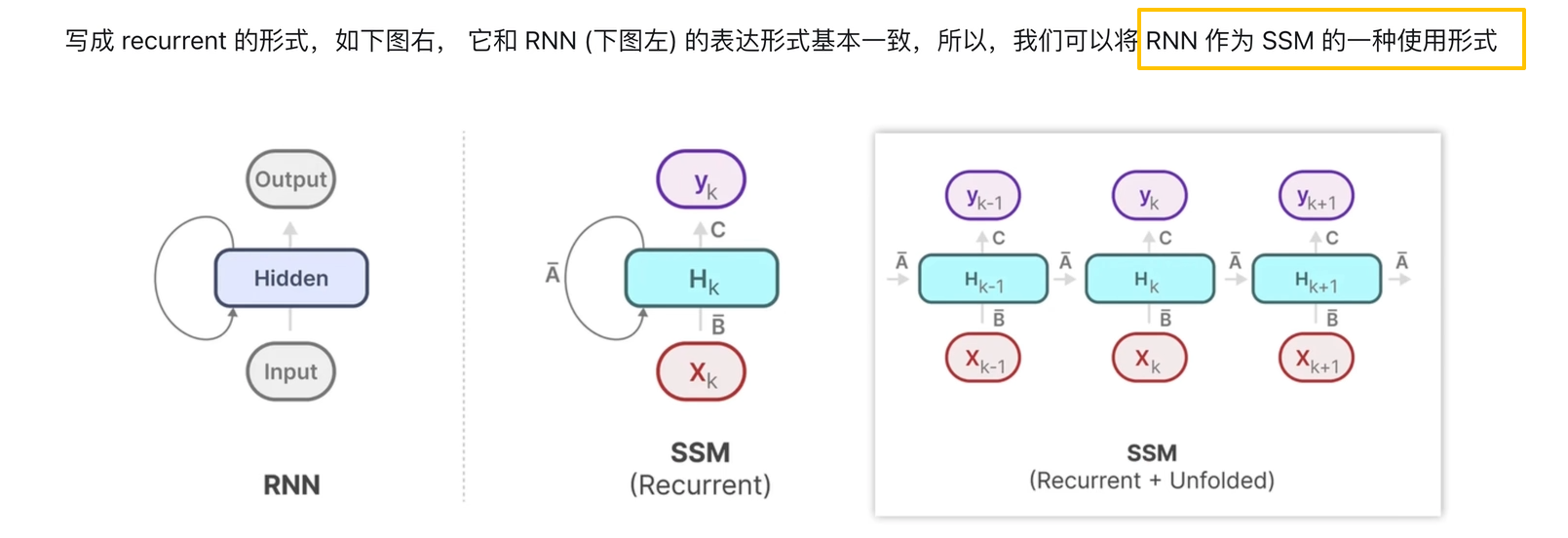
2.訓練階段使用SSM的卷積表示，推理階段使用RNN的表示

 SSM的卷積表示

卷積知識：

 

 

 把SSM公式用卷積形式表示

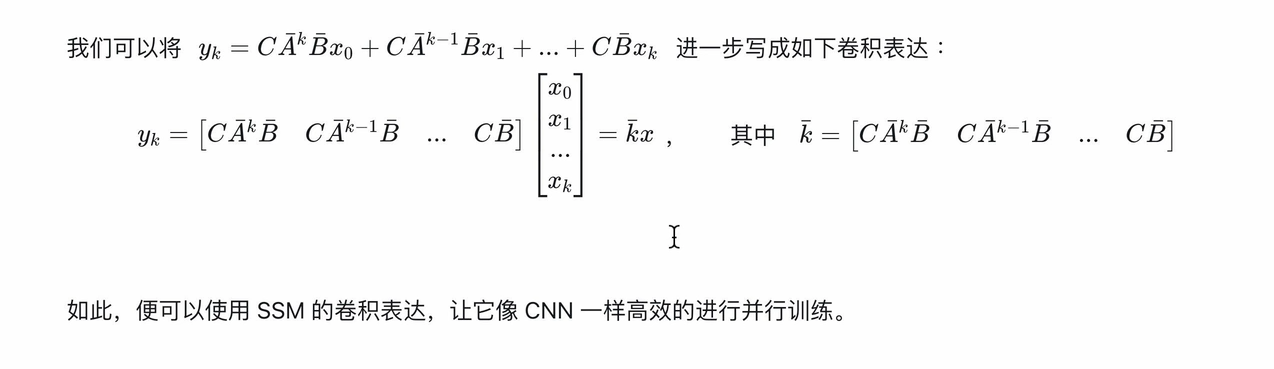
3.使用Hippo矩陣減小計算復雜度（即S4參數化），解決長距離依賴問題

A：

 

 

 

 

 

 LTI局限性

從循環的角度來看，它們的恒定動態，無法讓它們從上下文中選擇正確的信息，也無法以依賴于輸入的方式影響沿序列傳遞的隱藏狀態。

從卷積的角度來看，眾所周知，全局卷積可以解決普通的復制任務 ，因為它只需要時間感知，但由于缺乏內容感知，它們難以完成選擇性復制任務。更具體地說，輸入到輸出之間的間隔是變化的，無法用靜態卷積核建模。

總而言之，序列模型的效率與有效性權衡取決于它們壓縮狀態的能力：高效的模型必須具有較小的狀態，而有效的模型必須具有包含來自上下文的所有必要信息的狀態。反過來，我們提出構建序列模型的一個基本原則是選擇性：或者說，一種感知上下文的能力，能夠聚焦或過濾掉序列狀態中的輸入。具體來說，選擇機制控制著信息如何在序列維度上傳播或交互

選擇性SSM

 圖的解釋

把 5 個輸入通道分別送進 5 個獨立的 SSM，每個 SSM 內部只把「當前真正需要」的 4 維潛在狀態 h 臨時拉到 GPU 高速緩存（SRAM）里算一圈，算完就扔，絕不占主存（HBM），靠「選擇機制」決定哪一段 h 才值得被實例化

 

通過“參數化SSM的輸入”，讓模型對信息有選擇性處理，以便關注或忽略特定的輸入。這樣一來，模型能夠過濾掉與問題無關的信息，并且可以長期記住與問題相關的信息

好比，Mamba每次參考前面所有內容的一個概括，越往后寫對前面內容概括得越狠，丟掉細節、保留大意

SSM的循環表示創建了一個非常高效的小狀態，因為它壓縮了整個歷史記錄。然而，與不壓縮歷史記錄（通過注意力矩陣）的Transformer模型相比，它的功能要弱得多。

Mamba的目標是實現兩全其美：創建一個像Transformer一樣強大的小狀態。Mamba通過有選擇地將數據壓縮到狀態中來實現這一目標。當輸入一個句子時，通常會包含一些沒有多大意義的信息，例如停用詞。為了有選擇地壓縮信息，我們需要參數依賴于輸入。為此，我們首先探討訓練期間SSM中輸入和輸出的維度。

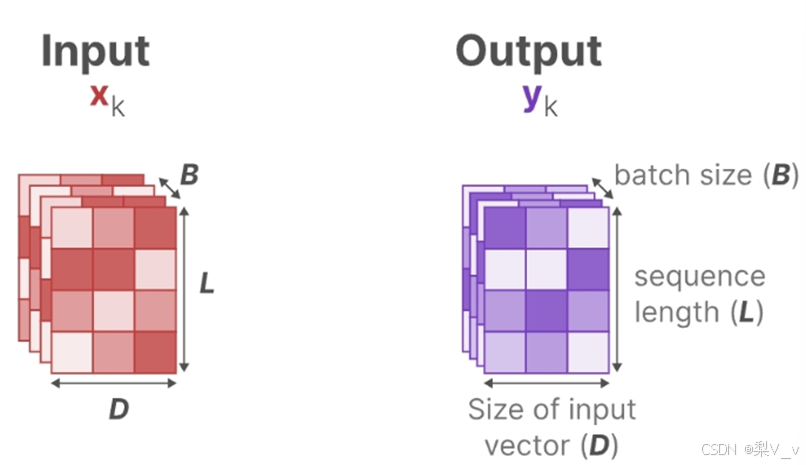
為了對批量大小為B，長度為L，具有D個通道的輸入序列??進行操作。總之，類似總計有B個序列，每個序列的長度為L，且每個序列中每個token的維度為D。

在結構化狀態空間模型 (S4) 中，矩陣A、B和C獨立于輸入，因為它們的維度N和D是靜態的并且不會改變。  A∈R^N×N,B∈R^N×1,C∈R^1×N矩陣都可以由??個數字表示。

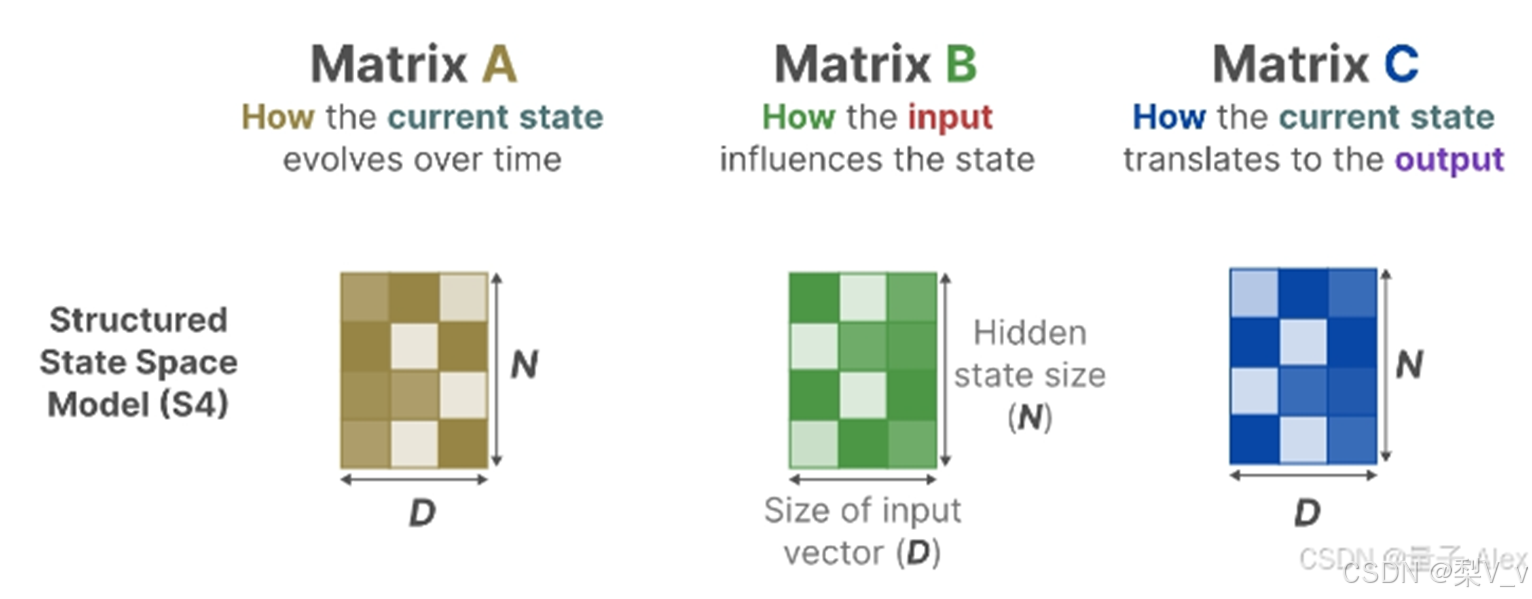
 從S4到S6的過程中 影響輸入的??矩陣、影響狀態的??矩陣的大小從原來的(D,N)變成了(B,L,N) batch size、sequence length、hidden state size

且Δ的大小由原來的D變成了(B,L,D)，意味著對于一個 batch 里的每個 token (總共有 BxL 個)都有一個獨特的Δ

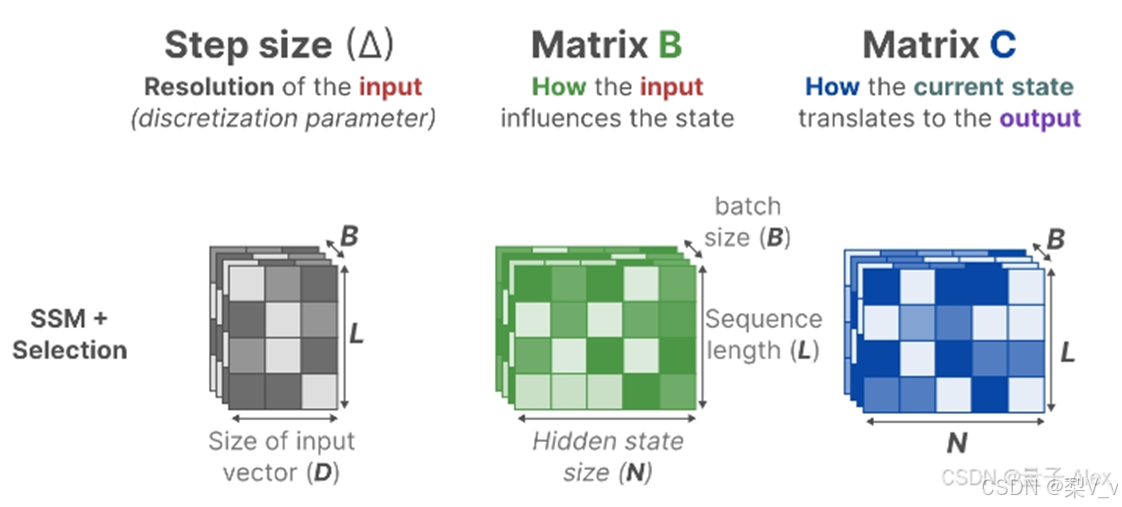
 Mamba通過合并輸入的序列長度和批量大小，使得矩陣B和C以及步長Δ都取決于輸入。這意味著對于每個輸入標記，我們現在有不同的B和C矩陣，可以解決內容感知問題！

A沒有變成依賴于輸入，但是離散化之后也是可變的，因為diate可變