學習與反思

主要是記錄自己遇到的問題以及踩的坑
同時歡迎各位大佬，給我提出意見，我一定會好好吸取。^_

準確率只有0.1左右？（or 很低）

• 有可能是因為權重沒有初始化（不一定是必要的）
• 或者學習率設置的問題，可能設置的太大了，試著調小一些

如何區(qū)分驗證集和測試集？

• 訓練集 （訓練階段）

用于構建我們的模型，我們的模型在訓練集上進行學習，通常在這個階段我們可以有多種方法進行訓練

• 驗證集 Validation Set（模型挑選階段）

用于挑選最優(yōu)模型超參的樣本集合：使用驗證集可以得到反向傳播什么時候結束以及超參怎么設置最合理，同時防止過擬合。主要目的是為了挑選在驗證集上表現(xiàn)最好的模型。

• 測試集 Test Set（驗證階段 評估泛化誤差）

在我們挑選好驗證集上表現(xiàn)最好的模型之后，用于評估該模型泛化能力的數(shù)據(jù)集。

如何訓練自己的數(shù)據(jù)集？

1. 首先獲取自己的數(shù)據(jù)，各類數(shù)據(jù)要相對均衡，以及圖片命名盡量不要使用中文
2. 劃分訓練集和測試集

數(shù)據(jù)集為什么要進行歸一化？

數(shù)據(jù)歸一化（Normalization）是數(shù)據(jù)預處理中的一個重要步驟，尤其在機器學習和深度學習中。 它將數(shù)據(jù)縮放到一個統(tǒng)一的范圍（通常是 [0, 1] 或 [-1, 1]），從而提高模型的訓練效率和性能。

數(shù)據(jù)歸一化是深度學習中不可或缺的步驟，它通過調整數(shù)據(jù)的范圍和分布，幫助模型更快地收斂，減少數(shù)值計算問題，提高泛化能力，并簡化模型的設計和訓練。

圖形預處理

1. 尺寸變化
2. 格式轉換（變?yōu)門ensor格式）
3. 歸一化

為什么有時損失函數(shù)增加但是精度卻在上升？

在訓練深度學習模型時，有時會觀察到一個看似矛盾的現(xiàn)象：損失函數(shù)（Loss）在增加，
但精度（Accuracy）卻在上升。這種現(xiàn)象可能由多種原因引起，以下是一些可能的解釋：

1. 損失函數(shù)和精度的衡量方式不同

• 損失函數(shù)（Loss）：衡量的是模型輸出與真實標簽之間的差異，通常是一個連續(xù)的數(shù)值。常見的損失函數(shù)包括交叉熵損失（Cross-Entropy
  Loss）、均方誤差（MSE）等。損失函數(shù)越小，表示模型的預測越接近真實值。
• 精度（Accuracy）：衡量的是模型預測正確的比例，是一個離散的指標。例如，在分類任務中，精度是模型正確分類的樣本數(shù)占總樣本數(shù)的比例。
  原因：損失函數(shù)和精度的優(yōu)化目標不同。損失函數(shù)關注的是預測值與真實值之間的差異，而精度關注的是預測結果是否完全正確。因此，即使損失函數(shù)增加，模型的預測結果可能仍然足夠接近真實值，從而導致精度上升。

2. 數(shù)據(jù)不平衡或類別分布不均

• 如果數(shù)據(jù)集中某些類別占主導地位，模型可能會偏向于預測這些類別，從而導致?lián)p失函數(shù)增加，但精度仍然較高。

3. 模型過擬合

• 如果模型在訓練集上表現(xiàn)良好，但在驗證集上損失函數(shù)增加但精度上升，可能是因為模型過擬合了訓練集中的某些噪聲或異常值。

4. 學習率過高

• 如果學習率設置過高，模型的權重更新可能會過大，導致?lián)p失函數(shù)在某些迭代中增加。然而，如果模型的預測結果仍然接近真實值，精度可能不會受到影響。

5. 損失函數(shù)的選擇問題

• 不同的損失函數(shù)對誤差的敏感度不同。例如，交叉熵損失對概率值的微小變化非常敏感，而精度則只關注最終的分類結果。

6. 數(shù)據(jù)預處理或數(shù)據(jù)增強的影響
   -如果在訓練過程中使用了數(shù)據(jù)增強（如隨機裁剪、旋轉等），模型可能會在某些增強后的數(shù)據(jù)上表現(xiàn)不佳，導致?lián)p失函數(shù)增加。但如果這些增強后的數(shù)據(jù)對精度的影響較小，精度可能仍然較高。

7. 模型架構或正則化的影響

• 如果模型架構過于復雜，或者正則化不足，模型可能會在某些樣本上表現(xiàn)不佳，導致?lián)p失函數(shù)增加。但如果這些樣本對精度的影響較小，精度可能仍然較高。

8. 批量大小（Batch Size）的影響

• 如果批量大小設置得過大或過小，可能會導致?lián)p失函數(shù)和精度之間的不一致。

隨著層數(shù)的增加, 訓練誤差和測試誤差不降反增?

這是由于"退化問題"導致的, 退化問題最明顯的表現(xiàn)就是給網(wǎng)絡疊加更多的層之后, 性能卻快速下降的情況. 按照道理, 給網(wǎng)絡疊加更多的層,
淺層網(wǎng)絡的解空間是包含在深層網(wǎng)絡的解空間中的, 深層網(wǎng)絡的解空間至少存在不差于淺層網(wǎng)絡的解, 因為只需要將增加的層變成恒等映射,
其他層的權重原封不動復制淺層網(wǎng)絡, 就可以獲得和淺層網(wǎng)絡同樣的性能. 更好地解明明存在, 為什么找不到, 找到的反而是更差的解?

退化問題的原因可以總結為:

• 優(yōu)化難度隨著深度的增加非線性上升: 深層網(wǎng)絡擁有更多參數(shù), 解空間的維度和復雜性呈現(xiàn)指數(shù)級增長, 這使得優(yōu)化算法需要在一個更大的高維空間內找到最優(yōu)解,
  難度大大增加
• 誤差積累: 深層網(wǎng)路中的每一層都會對后續(xù)層的輸入產(chǎn)生影響, 如果某些層的輸出有輕微偏差, 這些偏差可能隨著層數(shù)的增加而累積放大,
  導致最終的誤差增大

大白話解釋：打個比方, 你有一張比別人更大的藏寶圖(解空間), 理論上你能找到更多的保障, 但是如果你沒有很好的工具(
優(yōu)化算法), 反而會因為地圖太復雜, 找不到最好的路徑, 結果挖了一些不值錢的東西(次優(yōu)解), 甚至挖錯地方.

為什么訓練集和測試集的精準度很高,而驗證集的精準度很低?

可能的原因是在model_train.py文件中
train_transform = transforms.Compose([transforms.Resize((224, 224)), transforms.ToTensor(), normalize])未加上最后的那個歸一化處理

LeakyReLU()和ReLU()函數(shù)的區(qū)別

• ReLU():x>0:輸出x；x<0，輸出0
• LeakyReLU():f(x):x>0，輸出x；x<0，輸出a*x（a表示一個很小的斜率值）

為什么要計算梯度？

計算梯度的主要目的是通過優(yōu)化算法調整模型的參數(shù)，以最小化損失函數(shù)。以下是具體原因：

（1）優(yōu)化模型參數(shù)

• 梯度是優(yōu)化算法（如梯度下降）的基礎。通過計算損失函數(shù)對每個參數(shù)的梯度，可以知道如何調整參數(shù)以減少損失。

• 例如，在梯度下降中，參數(shù)更新公式為：

  θnew=θold?η??L(θ)

  其中，η 是學習率（learning rate），表示每次更新的步長。

（2）找到損失函數(shù)的最小值

• 梯度指向損失函數(shù)增加最快的方向，而負梯度指向損失函數(shù)減少最快的方向。
• 通過沿著負梯度方向更新參數(shù)，可以逐步找到損失函數(shù)的最小值。

（3）自動微分

• 神經(jīng)網(wǎng)絡的訓練涉及復雜的函數(shù)組合，手動計算梯度非常困難且容易出錯。
• PyTorch 和 TensorFlow 等深度學習框架通過自動微分（Automatic Differentiation）技術，自動計算梯度，大大簡化了訓練過程。

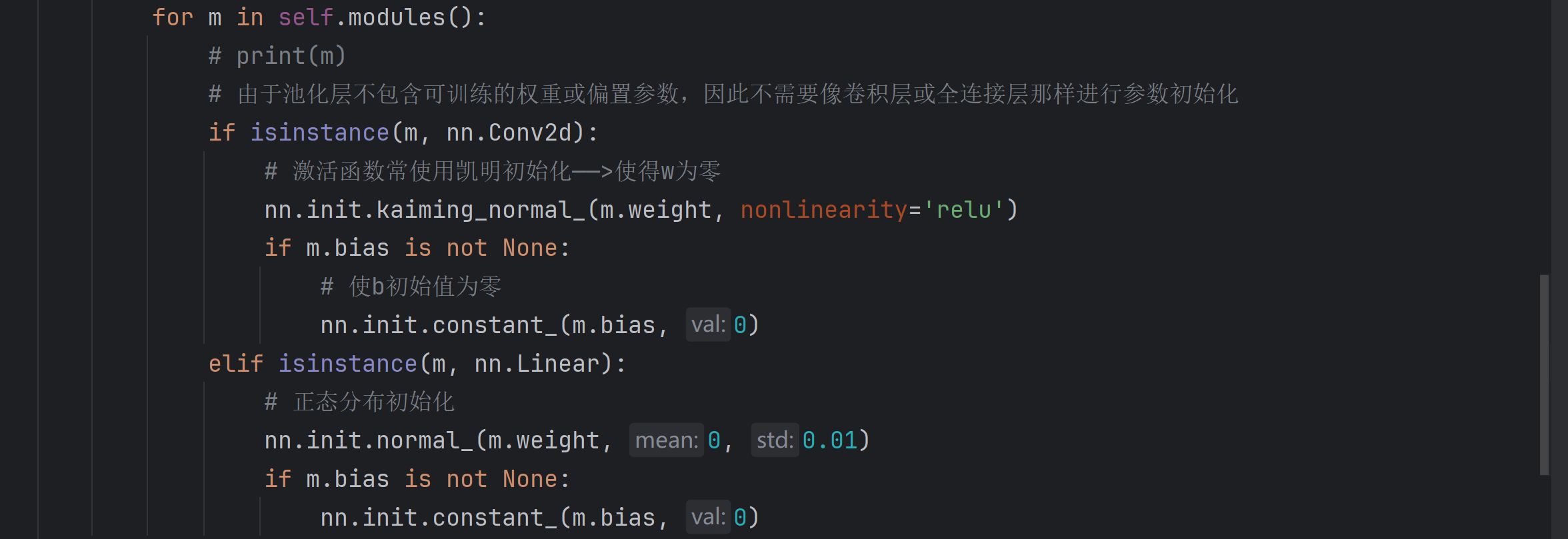
為什么有時需要權重初始化？

• 避免梯度消失或爆炸。
• 加速模型收斂。
• 打破對稱性，使每個神經(jīng)元能夠學習不同的特征。
• 提高模型的最終性能。

示例：

常見的損失函數(shù)及其適用領域和任務的詳細說明:

1. 均方誤差（MSE）

• 定義：
  • 衡量預測值與真實值之間差的平方的平均值。
• 適用領域和任務：
  • 回歸問題：適用于預測連續(xù)數(shù)值的任務，例如房價預測、股票價格預測等。
  • 數(shù)據(jù)分布相對均勻，沒有明顯的異常值。
  • 需要對較大的誤差進行更嚴厲的懲罰。
• 特點：
  • 數(shù)學上易于處理，優(yōu)化效果好。
  • 對異常值非常敏感。

2. 平均絕對誤差（MAE）

• 定義：
  • 衡量預測值與真實值之間差的絕對值的平均值。
• 適用領域和任務：
  • 回歸問題：適用于預測連續(xù)數(shù)值的任務。
  • 數(shù)據(jù)中存在異常值。
  • 需要對所有誤差進行相同程度的懲罰。
• 特點：
  • 對異常值不敏感。
  • 數(shù)學上不如MSE易于處理。

3. Huber 損失

• 定義：
  • 結合了MSE和MAE的優(yōu)點，在誤差較小時類似于MSE，在誤差較大時類似于MAE。
• 適用領域和任務：
  • 回歸問題：適用于預測連續(xù)數(shù)值的任務。
  • 數(shù)據(jù)中可能存在異常值。
  • 需要在對小誤差的敏感性和對大誤差的魯棒性之間取得平衡。
• 特點：
  • 對異常值具有一定的魯棒性。
  • 需要設置一個超參數(shù)。

4. 交叉熵損失（Cross-Entropy Loss）

• 定義：
  • 衡量兩個概率分布之間的差異。
• 適用領域和任務：
  • 分類問題：適用于預測類別標簽的任務，例如圖像分類、文本分類等。
  • 特別適用于多分類問題。
• 特點：
  • 在分類問題中表現(xiàn)良好。
  • 對預測錯誤的懲罰力度較大。

5. 二元交叉熵損失（Binary Cross-Entropy Loss）

• 定義：
  • 交叉熵損失的特殊情況，適用于二分類問題。
• 適用領域和任務：
  • 二分類問題：適用于預測兩個類別標簽的任務，例如垃圾郵件檢測、疾病診斷等。
• 特點：
  • 在二分類問題中表現(xiàn)良好。
  • 對預測錯誤的懲罰力度較大。

6. KL 散度（Kullback-Leibler Divergence）

• 定義：
  • 衡量一個概率分布與另一個概率分布之間的差異。
• 適用領域和任務：
  • 生成模型：適用于訓練生成模型，例如變分自編碼器（VAE）、生成對抗網(wǎng)絡（GAN）等。
  • 概率分布估計。
• 特點：
  • 不對稱性。
  • 在生成模型中廣泛應用

好的，以下是一些常見的損失函數(shù)及其適用領域和任務的詳細說明：

1. 均方誤差（MSE）

• 定義：
  • 衡量預測值與真實值之間差的平方的平均值。
• 適用領域和任務：
  • 回歸問題：適用于預測連續(xù)數(shù)值的任務，例如房價預測、股票價格預測等。
  • 數(shù)據(jù)分布相對均勻，沒有明顯的異常值。
  • 需要對較大的誤差進行更嚴厲的懲罰。
• 特點：
  • 數(shù)學上易于處理，優(yōu)化效果好。
  • 對異常值非常敏感。

2. 平均絕對誤差（MAE）

• 定義：
  • 衡量預測值與真實值之間差的絕對值的平均值。
• 適用領域和任務：
  • 回歸問題：適用于預測連續(xù)數(shù)值的任務。
  • 數(shù)據(jù)中存在異常值。
  • 需要對所有誤差進行相同程度的懲罰。
• 特點：
  • 對異常值不敏感。
  • 數(shù)學上不如MSE易于處理。

3. Huber 損失

• 定義：
  • 結合了MSE和MAE的優(yōu)點，在誤差較小時類似于MSE，在誤差較大時類似于MAE。
• 適用領域和任務：
  • 回歸問題：適用于預測連續(xù)數(shù)值的任務。
  • 數(shù)據(jù)中可能存在異常值。
  • 需要在對小誤差的敏感性和對大誤差的魯棒性之間取得平衡。
• 特點：
  • 對異常值具有一定的魯棒性。
  • 需要設置一個超參數(shù)。

4. 交叉熵損失（Cross-Entropy Loss）

• 定義：
  • 衡量兩個概率分布之間的差異。
• 適用領域和任務：
  • 分類問題：適用于預測類別標簽的任務，例如圖像分類、文本分類等。
  • 特別適用于多分類問題。
• 特點：
  • 在分類問題中表現(xiàn)良好。
  • 對預測錯誤的懲罰力度較大。

5. 二元交叉熵損失（Binary Cross-Entropy Loss）

• 定義：
  • 交叉熵損失的特殊情況，適用于二分類問題。
• 適用領域和任務：
  • 二分類問題：適用于預測兩個類別標簽的任務，例如垃圾郵件檢測、疾病診斷等。
• 特點：
  • 在二分類問題中表現(xiàn)良好。
  • 對預測錯誤的懲罰力度較大。

6. KL 散度（Kullback-Leibler Divergence）

• 定義：
  • 衡量一個概率分布與另一個概率分布之間的差異。
• 適用領域和任務：
  • 生成模型：適用于訓練生成模型，例如變分自編碼器（VAE）、生成對抗網(wǎng)絡（GAN）等。
  • 概率分布估計。
• 特點：
  • 不對稱性。
  • 在生成模型中廣泛應用。

選擇損失函數(shù)的建議：

• 根據(jù)任務類型選擇：回歸問題選擇MSE、MAE或Huber損失，分類問題選擇交叉熵損失。
• 考慮數(shù)據(jù)特征：如果數(shù)據(jù)存在異常值，選擇MAE或Huber損失。
• 嘗試多種損失函數(shù)：比較不同損失函數(shù)的性能，選擇最適合任務的損失函數(shù)。

--from Gemini by lzz

獨家技巧

• 一般情況：在大多數(shù)CNN架構中，平均池化層后面通常會跟一個平展層，因為平展后的特征通常用于全連接層的輸入，進行分類或回歸任務。
• 注意:bn層里面放前一個通道數(shù)的大小
• 全連接層（Fully Connected Layer）和卷積層（Convolutional Layer）后一般會跟著一個激活函數(shù)（Activation Function）。
• 在 PyTorch 中，當你創(chuàng)建一個 nn.Module 的實例時，例如 self.c1 = Conv_Block(3, 64)，這會調用 Conv_Block 類的 init
  方法，初始化模塊的參數(shù)。而當你調用模塊實例，例如 R1 = self.c1(x)，這會自動調用 Conv_Block 類的 forward 方法，執(zhí)行前向傳播邏輯。
• 必備公式：OH=(H+2*P-FH)/S+1；其中OH是計算后的高度，H是計算前的高度，F(xiàn)H是卷積和的高度。
• 在Gan網(wǎng)絡中，判別器中的激活函數(shù)推薦使用LeakyReLU()，可以保留一定的梯度信息
• 在交叉熵損失中我們一般使用BECLoss()函數(shù)；交叉熵損失函數(shù)（Cross-Entropy Loss）常用于分類任務，尤其是二分類任務（Binary Cross-Entropy Loss，簡稱 BCELoss）和多分類任務（Categorical Cross-Entropy Loss）
• len(dataloader)返回批次數(shù)，len(dataset)返回樣本數(shù)
• 注意：nn.imshow() 默認期望的范圍是 [0, 1] 或 [0, 255]
• 在數(shù)據(jù)加載的時候，訓練階段需要shuffle=True。而驗證和測試階段為shuffle=False，因為保持數(shù)據(jù)的原始順序可以方便地與真實標簽進行對比，從而更準確地評估模型的性能。