回憶中學(xué)的函數(shù)
這篇文章,帶你一次性回顧中學(xué)時(shí)代里的那些函數(shù)。如果對(duì)初中、高中的函數(shù)還記憶模糊,建議往下翻一翻。
一、函數(shù)的意義
如果說(shuō),學(xué)數(shù)學(xué)的核心就在于學(xué)習(xí)函數(shù),應(yīng)該沒(méi)有人會(huì)不同意吧。

數(shù)學(xué)應(yīng)用的目的是求解現(xiàn)實(shí)中的各種問(wèn)題,其中,為了模擬這種 "已知 xxx, 那么xxx" 論述的過(guò)程,函數(shù)是最重要的形式。通俗點(diǎn)說(shuō),函數(shù)就像一個(gè)“機(jī)器”:你輸入一個(gè)值,它按照規(guī)則處理后輸出一個(gè)結(jié)果
函數(shù)的定義通常記為:
其中,x 叫自變量,y 是因變量,大致的意思就是 y 隨著 x 的變化而變化,或者說(shuō) y 的取值和 x 離不開(kāi)干系。
那么 f(x) 描述的就是這種關(guān)系本身,即通過(guò) x 要怎樣推斷出 y 的值。
要素
嚴(yán)格說(shuō),函數(shù)包含三個(gè)要素,如下面的示例函數(shù):
- 要素1, 定義域, x 的取值范圍,如 \(x \in \mathbb{R}\)
- 要素2, 值域,y 也就是 f(x) 的結(jié)果取值范圍, 如 \(y \in \mathbb{R}\)
- 要素3, 計(jì)算法則,即 f(x) 公式本身
特征
既然函數(shù)描述了數(shù)據(jù)之間的關(guān)系,而現(xiàn)實(shí)場(chǎng)景中數(shù)據(jù)的關(guān)系會(huì)存在一些規(guī)律,這些規(guī)律通過(guò)圖像特征也能夠直觀的看出。一些常見(jiàn)的規(guī)律就包括:
單調(diào)性
函數(shù)單調(diào)性描述的是函數(shù)值隨著自變量的變大是變大還是變小,如單調(diào)遞增或遞減。
舉例:我們的愿望是,?? 工資和自己工作年限的關(guān)系是單調(diào)遞增,工作越久,工資越高。
奇偶性
奇偶性描述的是函數(shù)在正負(fù)方向上的對(duì)稱(chēng)性,例如當(dāng)x為2和-2時(shí),y=4則為偶函數(shù),若y=4和-4則為奇函數(shù)
舉例:我是一面鏡子,也是一個(gè)偶函數(shù)。
對(duì)稱(chēng)性
函數(shù)圖像是否在某個(gè)軸或點(diǎn)上呈現(xiàn)對(duì)稱(chēng)結(jié)構(gòu),可以認(rèn)為奇偶性是特殊的對(duì)稱(chēng)性。
舉例:蝴蝶的翅膀是左右對(duì)稱(chēng)的。
周期性
周期性表示函數(shù)的圖像或數(shù)值每隔一段時(shí)間,會(huì)重復(fù)一次
舉例:鐘表的指針運(yùn)動(dòng)、日出日落、心跳波形等等。
二、初階函數(shù)
1. 一次函數(shù)
一次函數(shù)的公式如下:
- k 是斜率(不能為 0),表示函數(shù)的變化速度;
- b 是常數(shù),表示圖像在 y 軸上的截距。
當(dāng) b = 0 時(shí),函數(shù)變?yōu)?y = kx,是一個(gè)正比例函數(shù)。
在幾何上,一次函數(shù)是一條直線,如下:
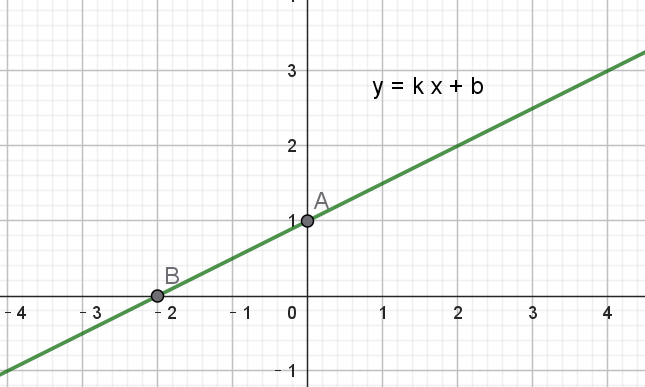
函數(shù)特征
| 特征項(xiàng) | 描述說(shuō)明 |
|---|---|
| ?? 圖像形狀 | 一條直線 |
| ?? 斜率 k | 決定直線的傾斜方向和陡峭程度 |
| ?? 截距 b | 決定圖像與 y 軸的交點(diǎn)位置 |
| ?? 單調(diào)性 | 當(dāng) k>0,函數(shù)遞增;當(dāng) k<0,函數(shù)遞減 |
| ?? 象限分布 | 根據(jù) k 和 b 的符號(hào),圖像穿過(guò)不同象限 |
應(yīng)用示例
假定你是一家小商店老板,需要做整體成本計(jì)算
- 表達(dá)式:\(y =5x+100\)
- 含義:x 代表 每件商品成本為 5 元,固定成本為 100 元。
2. 反比例函數(shù)
反比例函數(shù)的公式如下:
- k 是常數(shù),且 \(x≠0\)
反比例函數(shù)的圖像是一條雙曲線,如下:
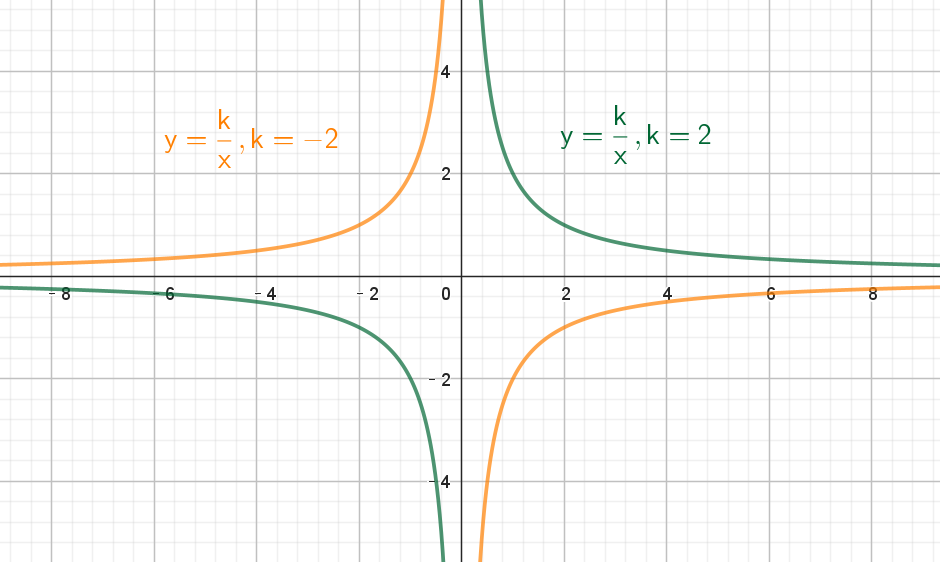
當(dāng) k > 0 時(shí),圖像位于第一象限和第三象限;
當(dāng) k < 0 時(shí),圖像位于第二象限和第四象限。
函數(shù)特征
| 特征項(xiàng) | 描述說(shuō)明 |
|---|---|
| ?? 圖像形狀 | 雙曲線,兩支分別位于對(duì)角象限 |
| ?? 單調(diào)性 | 在每個(gè)象限內(nèi)單調(diào)遞減 |
| ?? 不連續(xù)點(diǎn) | 在 x=0 處無(wú)定義,圖像斷裂 |
| ?? 對(duì)稱(chēng)性 | 關(guān)于原點(diǎn)中心對(duì)稱(chēng) |
| ?? 漸近線 | x軸和y軸是漸近線,圖像無(wú)限接近但不相交 |
應(yīng)用示例
.工廠作業(yè)時(shí),計(jì)算工作效率與時(shí)間的關(guān)系
- 表達(dá)式:\(y = \frac{10}{x}\)
- 含義:完成同一任務(wù)所需時(shí)間 y 與工人數(shù) x 成反比。
- 舉例:10人完成任務(wù)需1小時(shí),5人則需2小時(shí)。
3. 二次函數(shù)
二次函數(shù)的公式如下:
- \(a \neq 0\),否則退化為一次函數(shù);
- b, c 為常數(shù)。
二次函數(shù)的圖像是一條拋物線,如下:

掌握二次函數(shù)需要理解判別式:
判別式的符號(hào)與二次函數(shù)的圖像特征有特定的關(guān)系,如下所示:

函數(shù)特征
| 特征項(xiàng) | 描述說(shuō)明 |
|---|---|
| ?? 圖像形狀 | 拋物線 |
| ?? 開(kāi)口方向 | a > 0 向上開(kāi)口,a<0 向下開(kāi)口 |
| ?? 頂點(diǎn)坐標(biāo) | \((-\frac{b}{2a}, \frac{4ac - b^2}{4a})\) |
| ?? 對(duì)稱(chēng)軸 | \(x = -\frac{b}{2a}\) |
| ?? 單調(diào)性 | 頂點(diǎn)左側(cè)遞減,右側(cè)遞增(或相反) |
| ?? 零點(diǎn) | 與 x 軸交點(diǎn)由判別式 \(\Delta = b^2 - 4ac\) 決定 |
應(yīng)用示例
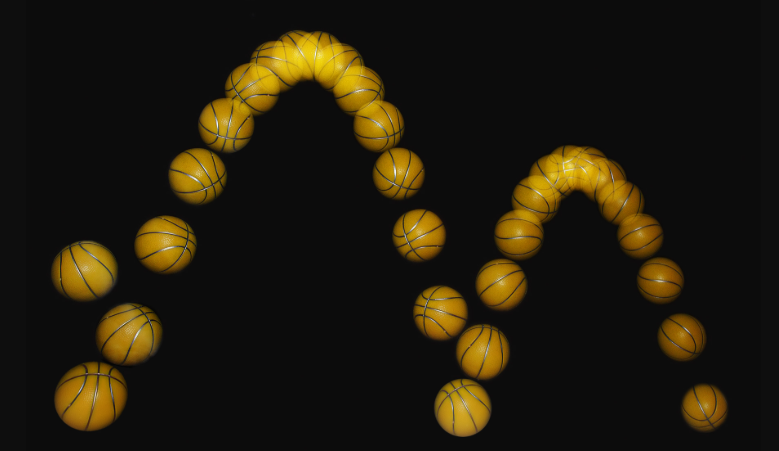
拋體運(yùn)動(dòng)高度計(jì)算,物體在豎直方向上,高度隨時(shí)間變化的關(guān)系。
-
表達(dá)式:\(y = -\frac{1}{2}gt^2 + v_0t + h_0\)
-
含義: g 是重力,v0 是初始速度,h0 是初始高度。
三、高階函數(shù)
4. 指數(shù)函數(shù)
指數(shù)函數(shù)的公式如下:
其中:
- a 是底數(shù),必須為正且不等于 1;
- 函數(shù)值 y 是底數(shù) a 的 x 次冪。
指數(shù)函數(shù)的圖像是一條光滑曲線,如下:

函數(shù)特征
| 條目 | 特征說(shuō)明 |
|---|---|
| ?? 增減性 | 當(dāng) a > 1 時(shí),函數(shù)遞增;當(dāng) 0<a<1 時(shí),函數(shù)遞減 |
| ?? 交點(diǎn) | 圖像恒過(guò)點(diǎn) (0, 1),因?yàn)?\(a^0 = 1\) |
| ?? 漸近線 | x 軸是水平漸近線,圖像無(wú)限接近但不相交 |
| ?? 定義域 | \((-\infty, +\infty)\),值域?yàn)?\((0, +\infty)\) |
| ?? 單調(diào)性 | 在整個(gè)定義域內(nèi)保持單調(diào)性,無(wú)極值點(diǎn) |
應(yīng)用示例

金融場(chǎng)景下,利用指數(shù)函數(shù)進(jìn)行復(fù)利計(jì)算:
- 表達(dá)式:\(A = P(1 + r)^n\)
- 含義:本金 P 在利率 r 下經(jīng)過(guò) n 期后的總額。
5. 對(duì)數(shù)函數(shù)
對(duì)數(shù)函數(shù)可看作是指數(shù)函數(shù)的反過(guò)程,對(duì)數(shù)函數(shù)的定義如下:
- 底數(shù) a 的多少次冪等于 x,即 \(a^y = x\)
- a是底數(shù),必須為正且不等于 1
- x 是正數(shù),必須大于 0
- y 是以 a 為底的 x 的對(duì)數(shù)
對(duì)數(shù)函數(shù)的圖像是一條光滑曲線,和相應(yīng)的指數(shù)函數(shù)沿著 y=x 直線呈對(duì)稱(chēng)關(guān)系,如下:

函數(shù)特征
| 特征項(xiàng) | 描述說(shuō)明 |
|---|---|
| ?? 圖像形狀 | 曲線,呈現(xiàn)遞增或遞減 |
| ?? 單調(diào)性 | 當(dāng) a > 1,圖像遞增;當(dāng) 0 < a < 1,圖像遞減 |
| ?? 交點(diǎn) | 恒過(guò)點(diǎn) (1, 0),因?yàn)?\(\log_a 1 = 0\) |
| ?? 漸近線 | y 軸(即x = 0)是垂直漸近線 |
| ?? 定義域 | x > 0,值域?yàn)?(?∞,+∞) |
應(yīng)用示例
碳-14測(cè)年法(Carbon-14 dating)是一種非常重要的放射性同位素測(cè)定技術(shù),可用來(lái)估算有機(jī)遺骸的年代。
當(dāng)生物死亡后,它就不再吸收碳,體內(nèi)的 \(^{14}C\) 開(kāi)始以固定速率衰減。通過(guò)測(cè)量遺骸中剩余的 \(^{14}C\) 含量,就可以推算出死亡時(shí)間。
- 表達(dá)式:\(N=N_0?e^{?λt}\),推出 \(t = \frac{1}{\lambda} \log_e \left( \frac{N_0}{N} \right)\)
- 含義: N0 是初始碳-14量值,N 是當(dāng)前值,λ 衰變常數(shù),e是自然對(duì)數(shù)。
6. 冪函數(shù)
冪函數(shù)的公式如下:
- a 是常數(shù)(通常為系數(shù));
- n 是冪指數(shù),可以是正數(shù)、負(fù)數(shù)、分?jǐn)?shù)甚至無(wú)理數(shù);
- 當(dāng) a = 1 時(shí),函數(shù)簡(jiǎn)化為 \(f(x) = x^n\),這是最常見(jiàn)的形式。
從幾何上看,冪函數(shù)的圖像形狀隨指數(shù) n 的不同而變化顯著,如下:

函數(shù)特征
| 冪指數(shù) n | 圖像特征說(shuō)明 |
|---|---|
| 正整數(shù)(偶數(shù)) | 圖像關(guān)于 y 軸對(duì)稱(chēng),開(kāi)口向上,如 \(y = x^2\) |
| 正整數(shù)(奇數(shù)) | 圖像關(guān)于原點(diǎn)對(duì)稱(chēng),穿過(guò)原點(diǎn),如 \(y = x^3\) |
| 分?jǐn)?shù)指數(shù) | 圖像在第一象限,如 \(y = \sqrt{x}\),定義域?yàn)?\(x \geq 0\) |
| 負(fù)整數(shù) | 圖像呈雙曲線狀,如 \(y = x^{-1}\),在 x = 0 處無(wú)定義 |
應(yīng)用示例
電功率公式:\(P = I^2 R\)
-
含義:其中 I是電流,R 是電阻。
-
說(shuō)明:該公式基于歐姆定律和功率公式結(jié)合得出,用于適用于電阻器、電熱器等純電阻負(fù)載的計(jì)算。
7. 絕對(duì)函數(shù)
絕對(duì)函數(shù)的公式如下:
- ∣x∣表示數(shù) x 到原點(diǎn)的距離;
- 當(dāng) \(x \geq 0\),∣x∣=x;
- 當(dāng) \(x<0\),|x| = -x。
絕對(duì)函數(shù)本質(zhì)上是一個(gè)分段函數(shù),在圖像上是一條“V” 型折線,如下:

函數(shù)特征
| 特征項(xiàng) | 描述說(shuō)明 |
|---|---|
| ?? 圖像形狀 | V 形折線,左右對(duì)稱(chēng) |
| ?? 單調(diào)性 | 左側(cè)遞減,右側(cè)遞增; |
| ?? 交點(diǎn) | 頂點(diǎn)在原點(diǎn) (0, 0),是圖像的轉(zhuǎn)折點(diǎn); |
| ?? 斜率 | 左側(cè)斜率為 -1,右側(cè)斜率為 +1; |
| ?? 定義域 | 最小值為 0,無(wú)最大值。 |
應(yīng)用示例
在評(píng)估傳感器數(shù)值的準(zhǔn)確度時(shí),經(jīng)常會(huì)使用 MAE 方法進(jìn)行誤差分析
- 表達(dá)式:\(\text{MAE} = \frac{1}{n} \sum_{i=1}^{n} |\text{測(cè)量值}_i - \text{真實(shí)值}_i|\)
- 含義:將多次歷史數(shù)據(jù)的測(cè)量值與真實(shí)值之間的誤差進(jìn)行平均計(jì)算,得到評(píng)估的準(zhǔn)確度。
8. Sigmoid函數(shù)
Sigmoid 函數(shù)(也稱(chēng)為 Logistic 函數(shù))是一種收斂函數(shù),適用于解決概率建模和二分類(lèi)問(wèn)題,也是機(jī)器學(xué)習(xí)和深度學(xué)習(xí)中常見(jiàn)的激活函數(shù)。
Sigmoid 函數(shù)的定義如下:
- e 是自然常數(shù)(約等于 2.718);
- 輸出值\(f(x) \in (0, 1)\),即將任意實(shí)數(shù)壓縮到 0 到 1 的區(qū)間。
從幾何上看,Sigmoid 函數(shù)是一個(gè)值介于0和1之間的漸進(jìn)式曲線,如下:
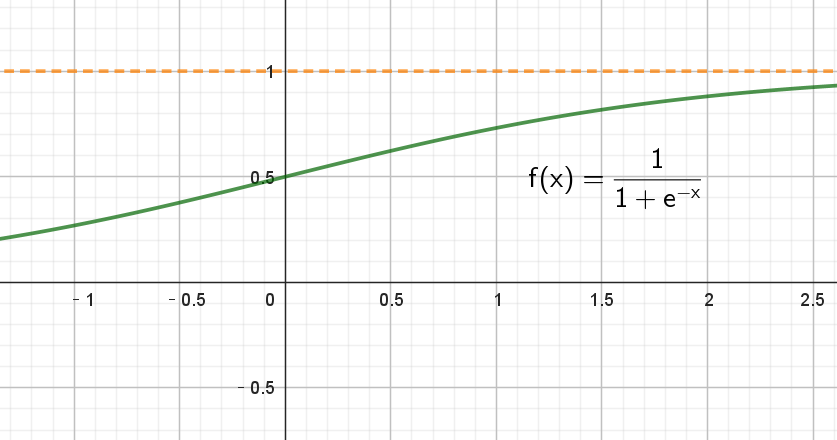
函數(shù)特征
| 特征項(xiàng) | 描述說(shuō)明 |
|---|---|
| ?? 單調(diào)性 | 函數(shù)在整個(gè)定義域上單調(diào)遞增 |
| ?? 對(duì)稱(chēng)性 | 圖像關(guān)于原點(diǎn)對(duì)稱(chēng) \(f(-x) = 1 - f(x)\) |
| ?? 極限值 | 當(dāng) \(x \to -\infty,f(x) \to 0\);當(dāng) \(x \to +\infty,f(x) \to 1\) |
| ?? 中心點(diǎn) | 當(dāng) x = 0,f(x)=0.5,圖像在此處最陡 |
| ?? 漸近線 | y 軸兩側(cè)分別有水平漸近線 y=0和 y=1 |
應(yīng)用示例

神經(jīng)網(wǎng)絡(luò)激活函數(shù)
- 用于隱藏層或輸出層,將神經(jīng)元輸出壓縮到 (0,1)(0, 1) 區(qū)間;
- 舉例:在二分類(lèi)問(wèn)題中,輸出值可解釋為屬于正類(lèi)的概率。
9. 三角函數(shù)
三角函數(shù)是數(shù)學(xué)中用于描述角與邊之間關(guān)系的基本函數(shù),廣泛應(yīng)用于幾何、物理、工程、天文等領(lǐng)域。
三角函數(shù)的公式如下:
| 函數(shù) | 圖像形狀 | 周期 | 振幅 | 對(duì)稱(chēng)性 |
|---|---|---|---|---|
| \(\sin x\) | 波浪形 | \(2\pi\) | 1 | 奇函數(shù),關(guān)于原點(diǎn)對(duì)稱(chēng) |
| \(\cos x\) | 波浪形 | \(2\pi\) | 1 | 偶函數(shù),關(guān)于 y 軸對(duì)稱(chēng) |
| \(\tan x\) | 間斷曲線 | \(\pi\) | 無(wú)界 | 奇函數(shù),關(guān)于原點(diǎn)對(duì)稱(chēng) |
函數(shù)特征

應(yīng)用示例

物理振動(dòng)建模,使用正弦波的數(shù)學(xué)表達(dá)式來(lái)描述物體振動(dòng)隨時(shí)間變化的波動(dòng)情況。
- 表達(dá)式:\(x(t) = A \sin(\omega t + \phi)\)
- 含義:\(\omega 是角頻率(波動(dòng)的快慢),t 是時(shí)間,\phi 是初始偏移,A 是振幅\)。
- 舉例:\(x(t)=5sin?(2πt),振幅為5米,\omega = 2\pi,即頻率為 1 Hz(每秒一周期),初始偏移為0\)
小結(jié)
函數(shù)是中學(xué)數(shù)學(xué)教材的主要學(xué)習(xí)和考試內(nèi)容,它同時(shí)也有著大量的實(shí)際場(chǎng)景應(yīng)用。在機(jī)器學(xué)習(xí)和深度學(xué)習(xí)領(lǐng)域,存在不少以函數(shù)為基礎(chǔ)的理論研究和實(shí)踐。但不幸的是,對(duì)大部分職場(chǎng)老鳥(niǎo)來(lái)說(shuō),這些內(nèi)容因時(shí)間和職業(yè)方向關(guān)系早已不再熟悉。本文對(duì)早期常見(jiàn)的一些基礎(chǔ)函數(shù)做了整理,旨在幫助快速回顧并建立一些基礎(chǔ)知識(shí)印象。

作者: 美碼師(zale)
出處: http://www.rzrgm.cn/littleatp/, 如果喜歡我的文章,請(qǐng)關(guān)注我的公眾號(hào)
本文版權(quán)歸作者和博客園共有,歡迎轉(zhuǎn)載,但未經(jīng)作者同意必須保留此段聲明,且在文章頁(yè)面明顯位置給出 原文鏈接 如有問(wèn)題, 可留言咨詢.

 浙公網(wǎng)安備 33010602011771號(hào)
浙公網(wǎng)安備 33010602011771號(hào)