向量那點(diǎn)事兒

一、向量

這次我們繼續(xù)聊一下向量。

向量可以理解為一個(gè)有方向的量。

它既有大小（長度），又有方向（指向哪里）。

生活中很多東西都可以用向量描述，比如：

• ?? 速度（你開車 60 km/h 向東）
• ??? 風(fēng)（風(fēng)速 5 m/s 向北）
• ?? 力（用 10 牛頓的力推箱子向右）

坐標(biāo)表示

在數(shù)學(xué)里，我們通常用坐標(biāo)來表示向量；而在幾何空間中，常常用箭頭來表示向量，箭頭的長度表示大小（模），方向表示向量的方向。

• 在二維空間中，一個(gè)向量表示如下：

其中 x 表示水平方向分量，y 表示豎直方向分量。
向量的模長為：\(|\vec{v}| = \sqrt{x^2 + y^2}\)

• 在三維空間中，一個(gè)向量表示如下：

其中 x, y, z 分別是沿三個(gè)坐標(biāo)軸的分量。
向量的模長為：\(|\vec{v}| = \sqrt{x^2 + y^2 + z^2}\)

• 在N維空間中，一個(gè)向量表示如下：

其中 x1...xn 分別是各個(gè)維度的分量。
向量的模長為：\(|\vec{v}| = \sqrt{x_1^2 + x_2^2 + \dots + x_n^2} \\\)

二、加減法

向量加法

設(shè)定：

那么有：

加法的幾何意義，可以使用三角形法則或平行四邊形法則來說明：

簡單的可以理解為，\(\vec{a}+\vec{b}\) 就是從坐標(biāo)原點(diǎn)沿著\(\vec{a}\)行進(jìn)后，再沿著\(\vec{b}\)行進(jìn)。

應(yīng)用示例

假定有兩股方向的力，如下：

\(\vec{F_1} = (3, 4), \quad \vec{F_2} = (1, 2)\)

那么這兩股力的合力為：

\(\vec{F} = \vec{F_1} + \vec{F_2} = (3+1, 4+2) = (4, 6)\)

向量減法

設(shè)定：

那么有：

加法的幾何意義，可以使用三角形法則或平行四邊形法則來說明：

簡單的可以理解為，\(\vec{a}-\vec{b}\) 就是從b的終點(diǎn)開始，朝著\(\vec{a}\)的終點(diǎn)行進(jìn)的向量。

應(yīng)用示例

在船的航行過程中，可以利用向量的減法來獲得船和水流的相對(duì)速度。

假定船的速度向量為：

\(\vec{v}_{船} = (8, 0) \quad (\text{向東 8 m/s})\)

水流速度向量為：

\(\vec{v}_{水} = (3, 1) \quad (\text{向東 3 m/s，向北 1 m/s})\)

那么船相對(duì)水流的速度向量為：

\(\vec{v}_{相對(duì)} = (8-3, 0-1) = (5, -1)\)

表示向東 5 m/s、向南 1 m/s。

三、向量內(nèi)積

向量的內(nèi)積又稱為點(diǎn)積（Dot Product），內(nèi)積是兩個(gè)向量對(duì)應(yīng)分量相乘后求和的一個(gè)標(biāo)量值。

設(shè)定：

那么有：

從幾何意義上講，向量的內(nèi)積還可以表示如下：

具體的證明可以參考下圖，將坐標(biāo)系進(jìn)行旋轉(zhuǎn)后，可完成推理：

其中 ?θ 表示兩個(gè)向量的夾角，根據(jù)余弦定理可以得出：

• 假定模長不變，夾角越小，內(nèi)積則越大
• 當(dāng)夾角為90度時(shí)（兩個(gè)向量垂直），此時(shí)內(nèi)積為0
• 內(nèi)積的本質(zhì)等同于向量的投影和模長的乘積
• 坐標(biāo)旋轉(zhuǎn)時(shí)，內(nèi)積保持不變

應(yīng)用示例

我們?cè)陔娚唐脚_(tái)上瀏覽產(chǎn)品詳情時(shí)，經(jīng)常會(huì)看到"相似產(chǎn)品"這樣的頁簽，其中會(huì)給我們推薦相關(guān)的產(chǎn)品。

這種商品推薦的場(chǎng)景便可以基于"余弦相似度"來實(shí)現(xiàn)，余弦相似度的核心是僅考慮向量的方向一致，忽略模長的影響。具體實(shí)現(xiàn)如下：

1. 將商品信息特征化表述，包括：

   • 類目
   • 品牌
   • 價(jià)格區(qū)間
   • 顏色 / 尺寸 / 材質(zhì)
   • 商品標(biāo)題/描述
   • 圖片特征

2. 特征向量歸一化

   上述的商品特征可以基于Embedding、CNN等算法來提取為特征值。

   這些特征值拼接后形成一個(gè)統(tǒng)一的商品向量，如下：

   \[\vec{g} = [x_{類目}, x_{品牌},x_{價(jià)格},x_{尺寸},x_{顏色},x_{圖譜特征}..] \]

   由于不同維度的特征值其模長無法統(tǒng)一，我們需要將其進(jìn)行歸一化（L2歸一）：

   對(duì)于其中的 \(x_k\)，其歸一后的值為：

   \[X_k = \frac{x_k}{\sqrt{x_1^2 + x_2^2 + \cdots + x_n^2}} \]

   L2歸一化使用歐幾里得范數(shù)來計(jì)算，最終得到特征向量為：

   \[\vec{G} = [X_{類目}, X_{品牌},X_{價(jià)格},X_{尺寸},X_{顏色},X_{圖譜特征}..] \]

   歸一化后，∥G∥=1，余弦相似度就簡化成兩個(gè)單位向量的點(diǎn)積，只比較方向（特征分布模式），消除了特征值大小的影響。

3. 計(jì)算商品特征向量的相似度，獲得最相似的N個(gè)商品

   通過計(jì)算向量的點(diǎn)積來比較相似度：$ simulaty = \vec{G} \cdot \vec{G2}$

向量點(diǎn)積在機(jī)器學(xué)習(xí)中常用于評(píng)估特征的方向相似性

四、向量外積

向量的外積又稱為叉積（Cross Product），兩個(gè)向量的外積是一個(gè)同時(shí)垂直于兩者的向量。

設(shè)定：

那么有：

• 向量 \(\vec{c}\)的模長：$\vec{c} = ∣\vec{a}∣∣\vec{b}∣sin?θ $，在幾何意義上等同與兩個(gè)向量為邊的平行四邊形的面積。

• 向量 \(\vec{c}\)的方向：垂直于兩個(gè)向量構(gòu)成的平面。

如下圖所示：

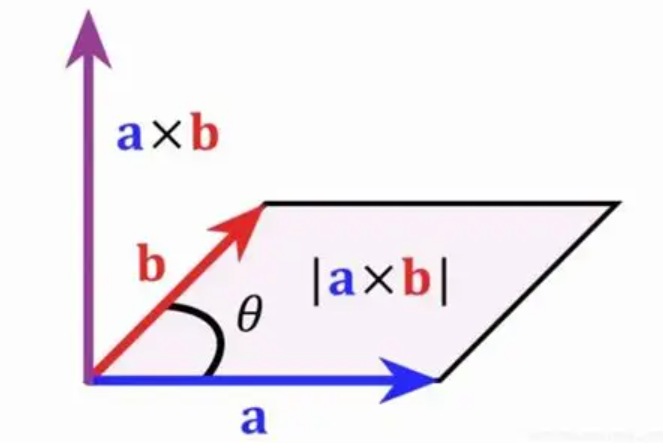
向量 \(\vec{c}\)的方向除了垂直之外，還需要遵循右手螺旋定則，也就是對(duì)于 \(\vec{a} × \vec{b} = \vec{c}\) 來說，右手四指方向從 a 轉(zhuǎn)向 b，大拇指所指方向就是 c 的方向。所以， \(\vec{a} × \vec{b}\) 和 \(\vec{b} × \vec{a}\) 的結(jié)果是相反的，即向量外積不滿足交換律。

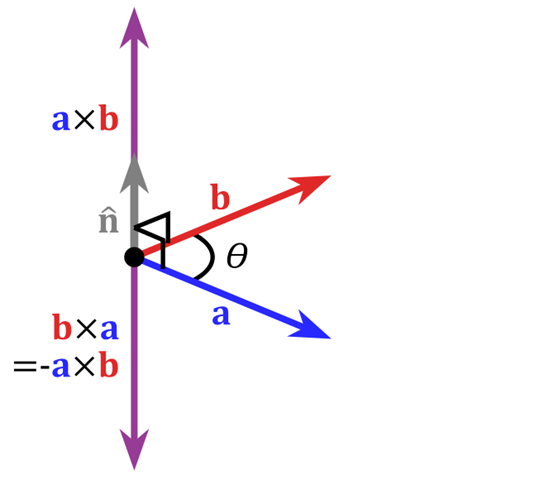
從幾何圖形上看，向量的外積可以垂直于兩個(gè)向量組成的平面，當(dāng)向量平行（共線）時(shí)，向量的外積為0。

需要注意的是，向量的外積僅適用于三維圖形，在四維及更高維空間中，垂直于兩個(gè)向量的方向不唯一，而是一個(gè)高維子空間，因此無法用一個(gè)單一向量來表示。

應(yīng)用示例

物理學(xué)上，我們通過力矩（Torque）來描述一種"讓物體轉(zhuǎn)起來的能力"。

比如：

你用扳手?jǐn)Q螺絲，用力的大小、角度和離螺絲中心的距離都會(huì)影響擰動(dòng)的效果。

同樣的力，扳手越長（離中心越遠(yuǎn)），越容易擰動(dòng)——因?yàn)榱馗蟆?/p>

力矩的公式如下：

• r 是從旋轉(zhuǎn)中心到施力點(diǎn)的位置向量

• ??：施加的作用力

力矩是向量 r 和向量 F的外積向量：

• 力矩的方向：由右手定則決定，表示旋轉(zhuǎn)軸的方向

• 力矩的大小：等于 \(|\vec{r}| \cdot |\vec{F}| \cdot \sin\theta\)，也就是力度、垂直距離、和角度三者疊加的結(jié)果。

五、小試牛刀

下面使用 numpy 來實(shí)現(xiàn)本文提到的向量加減法、向量內(nèi)積和外積計(jì)算。

代碼示例

import numpy as np

# 定義兩個(gè)三維向量
a = np.array([3, 4, 0])
b = np.array([4, 0, 3])

# 1?? 向量加法
add = a + b
print("加法 a + b =", add)

# 2?? 向量減法
sub = a - b
print("減法 a - b =", sub)

# 3?? 向量內(nèi)積（點(diǎn)積）
dot = np.dot(a, b)
print("內(nèi)積 a · b =", dot)

# 4?? 特征歸一化（L2歸一）
a_norm = a / np.linalg.norm(a)
b_norm = b / np.linalg.norm(b)
print("歸一化后的 a =", a_norm)
print("歸一化后的 b =", b_norm)

# 5?? 歸一后的余弦相似度
cos_sim = np.dot(a_norm, b_norm)
print("歸一后的余弦相似度 =", cos_sim)

# 6?? 向量外積（叉積）
cross = np.cross(a, b)
print("外積 a × b =", cross)

執(zhí)行上述程序，輸出結(jié)果如下：

加法 a + b = [7 4 3]
減法 a - b = [-1  4 -3]
內(nèi)積 a · b = 12
歸一化后的 a = [0.6 0.8 0. ]
歸一化后的 b = [0.8 0.  0.6]
歸一后的余弦相似度 = 0.48
外積 a × b = [ 12  -9 -16]

六、小結(jié)

向量的概念早在中學(xué)數(shù)學(xué)、物理學(xué)中就已經(jīng)能接觸到了，理解向量和空間幾何的結(jié)合非常重要。從最簡單的加減法就能體會(huì)到基本相對(duì)量的價(jià)值；向量內(nèi)積更是各種推薦算法、特征相似度計(jì)算的基礎(chǔ)范式，向量外積在機(jī)械工程學(xué)中大行其道等等，這些無一證明了向量在現(xiàn)實(shí)的數(shù)學(xué)應(yīng)用中的重要地位。