運(yùn)動(dòng)恢復(fù)結(jié)構(gòu)(SFM)
運(yùn)動(dòng)恢復(fù)結(jié)構(gòu)
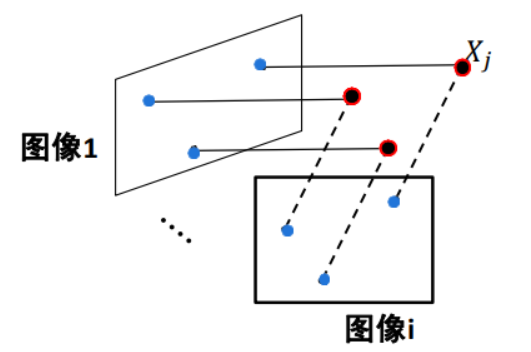
通過(guò)三維場(chǎng)景的多張圖片,恢復(fù)出該場(chǎng)景的三維結(jié)構(gòu)信息以及每張圖片對(duì)應(yīng)的攝像機(jī)參數(shù)。
已知:n個(gè)3D點(diǎn)\(X_j\)在m張圖像中的對(duì)應(yīng)點(diǎn)的像素坐標(biāo)\(x_{ij}\)\((i = 1, …, m, j = 1, …, n)\),且\(x_{ij} = M_iX_j\) \((i = 1,...,m,j=1,...,n)\)
其中,\(M_i\)是第i張圖片對(duì)應(yīng)的攝像機(jī)的投影矩陣
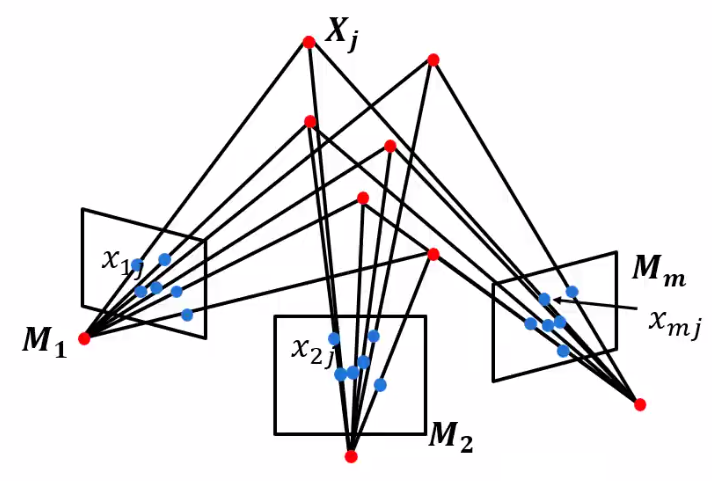
求解:
- m個(gè)攝像機(jī)投影矩陣\(M_i\)\((i = 1, … , m)\) \(\longrightarrow\) 運(yùn)動(dòng)(motion)
- n個(gè)三維點(diǎn)\(X_j(j=1,...,n)\)的坐標(biāo) \(\longrightarrow\) 結(jié)構(gòu)(structure)
三種典型的運(yùn)動(dòng)恢復(fù)結(jié)構(gòu)問(wèn)題
- 歐式結(jié)構(gòu)恢復(fù)(攝像機(jī)內(nèi)參數(shù)已知,外參數(shù)未知)
- 仿射結(jié)構(gòu)恢復(fù)(攝像機(jī)為仿射相機(jī),內(nèi)、外參數(shù)均未知)
- 透視結(jié)構(gòu)恢復(fù)(攝像機(jī)為透視相機(jī),內(nèi)、外參數(shù)均未知)
歐式結(jié)構(gòu)恢復(fù)
已知:
-
n個(gè)三維點(diǎn)\(X_j(j = 1, ..., n)\)在\(m\)張圖像中的對(duì)應(yīng)點(diǎn)的像素坐標(biāo)\(x_{ij}\)
-
m張圖像對(duì)應(yīng)的攝像機(jī)內(nèi)參數(shù)矩陣\(K_i(i=1,...,m)\)
且 \(x_{ij} = M_iX_j = K_i[R_i\quad T_i]X_j \qquad i = 1,..., m; j = 1, ..., n\)
其中\(m\)為圖像個(gè)數(shù),\(n\)為3D點(diǎn)個(gè)數(shù),\(M_i,K_i,[R_i\quad T_i]\)為第\(i\)張照片對(duì)應(yīng)的攝像機(jī)的投影矩陣、內(nèi)參數(shù)及外參數(shù)矩陣
求解
- n個(gè)三維點(diǎn)\(X_j(j = 1,...,n)\)的坐標(biāo)
- m個(gè)攝像機(jī)外參數(shù)\(R_i\)以及\(T_i\)\((i=1,...,m)\)
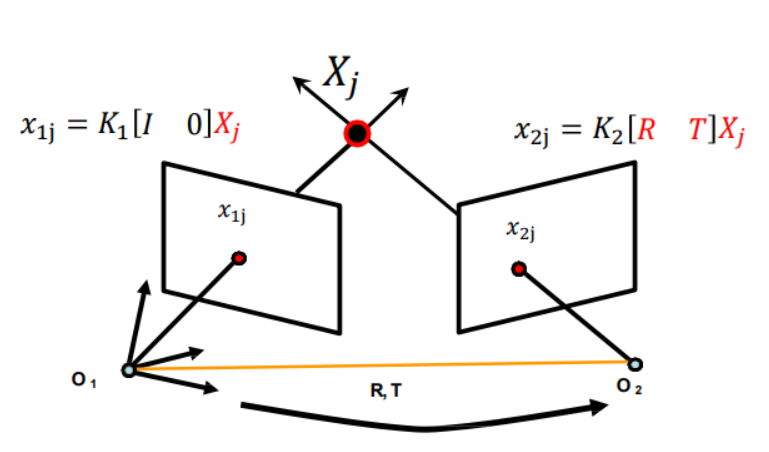
問(wèn)題:(2視圖)
求解:
-
求解基礎(chǔ)矩陣F
歸一化八點(diǎn)法
點(diǎn)的對(duì)應(yīng)關(guān)系:左圖和右圖進(jìn)行sift特征提取,對(duì)每一個(gè)特征點(diǎn)進(jìn)行描述,建立兩張圖的特征點(diǎn)的對(duì)應(yīng)關(guān)系。用RANSAC的方法去估計(jì)正確的變換矩陣從而剔除錯(cuò)誤點(diǎn)。
1、SIFT 2、匹配 3、RANSAC
如果正好8對(duì)點(diǎn),則只有唯一解,多于8對(duì)點(diǎn)則使用最小二乘求解
-
利用F與攝像機(jī)內(nèi)參數(shù)求解本質(zhì)矩陣E
\(E = K_2^TFK_1\)
-
分解本質(zhì)矩陣獲得R與T
\(E \longrightarrow R、T \longrightarrow M_2\)
-
三角化求解三維點(diǎn)\(X_j\)坐標(biāo)
\(X_j^* = \mathop{argmin}\limits_{X_j}(d(x_{1j},M_1X_j) + d(x_{2j},M_2X_j))\)
本質(zhì)矩陣分解
找到一個(gè)策略把E因式分解成兩部分
重要說(shuō)明:
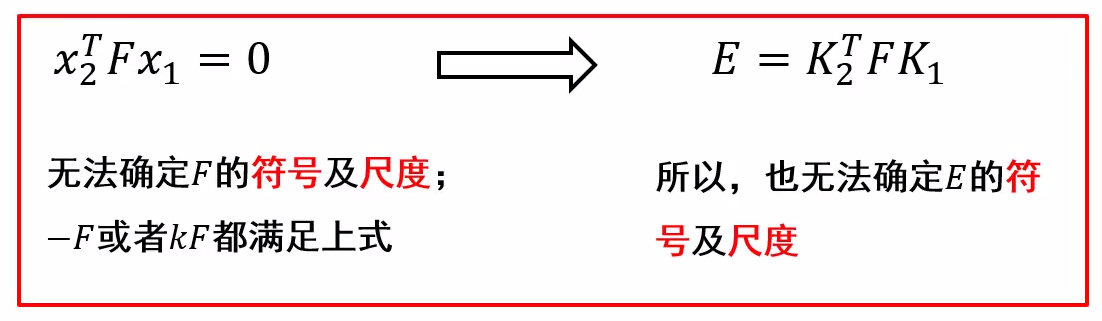
定義兩個(gè)矩陣:
重要性質(zhì):
在相差一個(gè)正負(fù)號(hào)的情況下
\([T_{\times}]\)可以寫成:\([T_{\times}] = kUZU^T\),其中\(U\)是單位正交陣,k是常數(shù)
不考慮符號(hào)、尺度,則
所以
同時(shí),對(duì)E進(jìn)行奇異值分解
與上面的進(jìn)行比較,發(fā)現(xiàn)可以把R表示出來(lái)
注意:E的這個(gè)因式分解只保證了矩陣\(UWV^T\)或\(UW^TV^T\)是正交的。其為旋轉(zhuǎn)矩陣還需確保行列式的值為正:
這樣R就為正,即為真正的旋轉(zhuǎn)矩陣
而怎么求解T呢?
由前面的\([T_{\times}] = UZU^T\)可以得到\(T \times T = [T_{\times}]T = UZU^TT = 0\),從而\(T = \pm u_3\)(U的第三列)
這里其實(shí)是相當(dāng)于\(AT = 0\),即\(T\)為\(A\)最小特征值對(duì)應(yīng)的特征向量,而\(A\)本質(zhì)上是SVD分解得到的\(UZU^T\),所以T就是\(U^T\)的最小特征值的特征向量,即為U的第三列
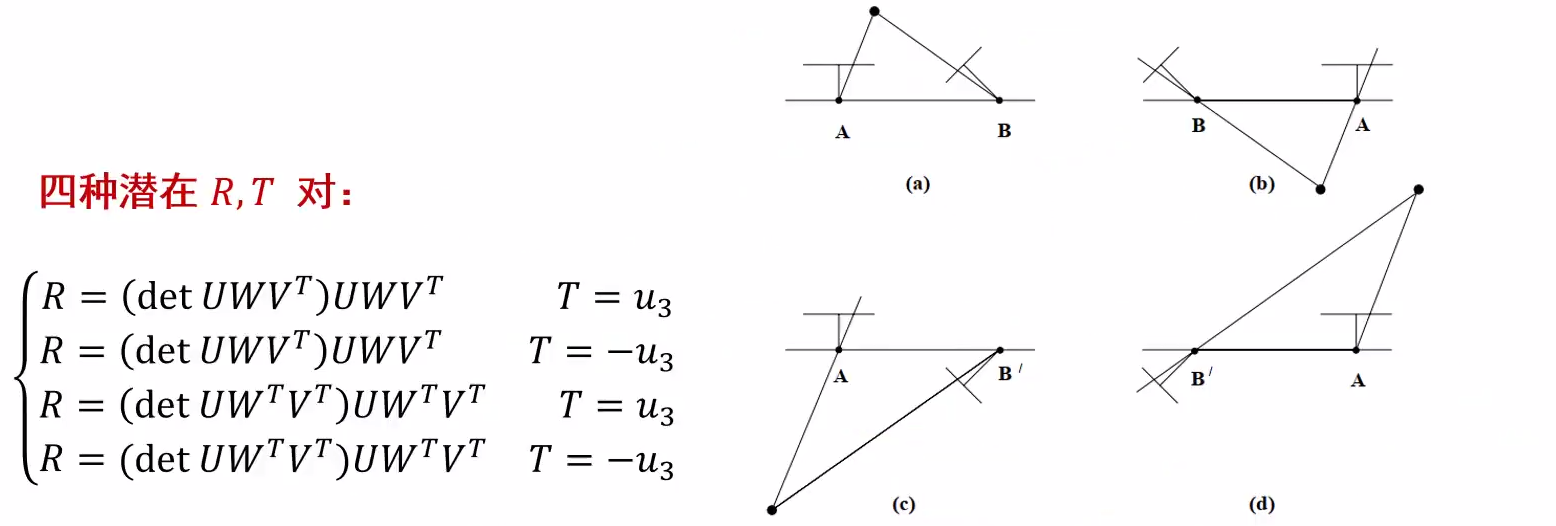
- 選擇一個(gè)點(diǎn)三角化,正確的一組解能保證該點(diǎn)在兩個(gè)攝像機(jī)的z坐標(biāo)均為正
- 對(duì)多個(gè)點(diǎn)進(jìn)行三角化,選擇在兩個(gè)攝像機(jī)系下z坐標(biāo)均為正的個(gè)數(shù)最多的那組R、T。(更魯棒)
做一個(gè)總結(jié):

歐式結(jié)構(gòu)恢復(fù)出的解沒有尺度概念,需要其他先驗(yàn)信息!
- 僅靠圖像去重建的三維場(chǎng)景與真實(shí)場(chǎng)景相差一個(gè)相似變換(旋轉(zhuǎn)、平移、縮放)
- 恢復(fù)的場(chǎng)景與真實(shí)場(chǎng)景之間僅存在相似變換的重構(gòu)稱為度量重構(gòu)
仿射結(jié)構(gòu)恢復(fù)

問(wèn)題:已知n個(gè)三維點(diǎn)\(X_j\)在m張圖像中的對(duì)應(yīng)點(diǎn)的像素坐標(biāo)\(x_{ij}\)\((i = 1, …, m, j = 1, …, n)\),且\(x_{ij} = A_iX_j+b_i\) \((i = 1,...,m,j=1,...,n)\)
? 其中,\(A_i,b_i\)組成了第i張圖片對(duì)應(yīng)的仿射攝像機(jī)的投影矩陣$M_i = \left[\begin{matrix}A_i & b_i \ 0 & 1\end{matrix}\right] $
求解:
- n個(gè)三維點(diǎn)\(X_j(j = 1,...,n)的坐標(biāo)\)
- m個(gè)仿射攝像機(jī)的投影矩陣\(A_i\)與\(b_i(i=1,...,m)\)
方法:
- 代數(shù)方法
- 因式分解法
- 數(shù)據(jù)中心化
- 因式分解
中心化:減去圖像點(diǎn)的質(zhì)心
i表示第i個(gè)攝像機(jī),\(x_{ij}\)表示第i個(gè)攝像機(jī)的第j個(gè)點(diǎn)
于是
如果3D點(diǎn)的質(zhì)心 = 世界坐標(biāo)系的中心,則\(\hat{x}_{ij} = A_i\hat{X}_j = A_iX_j\)
因式分解
把取均值后的\(m \times n\)個(gè)測(cè)量值寫成矩陣的形式:
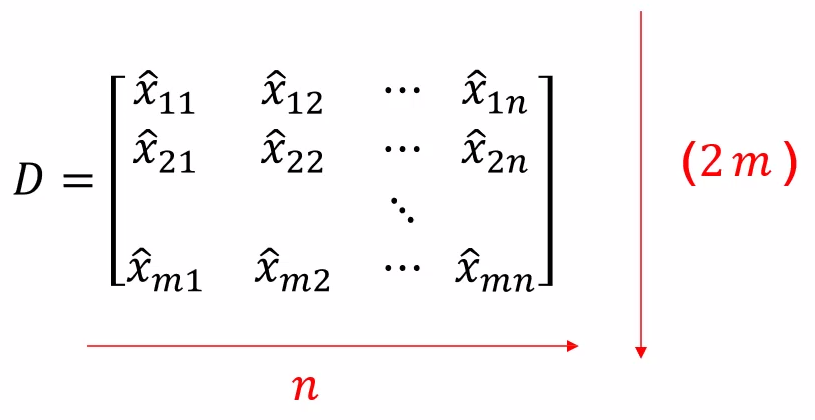
\(\left[\begin{matrix}x_{11} & x_{12} & \dots & x_{1n}\end{matrix}\right]^T\)是第一個(gè)相機(jī)下的點(diǎn),每個(gè)\(x_{ij}\)是一個(gè)\(2 \times 1\)的向量,為\([u\quad v]^T\),所以\(\hat{x}_{11} = [\overline{u}\quad \overline{v}]^T\)

怎么分解D呢?
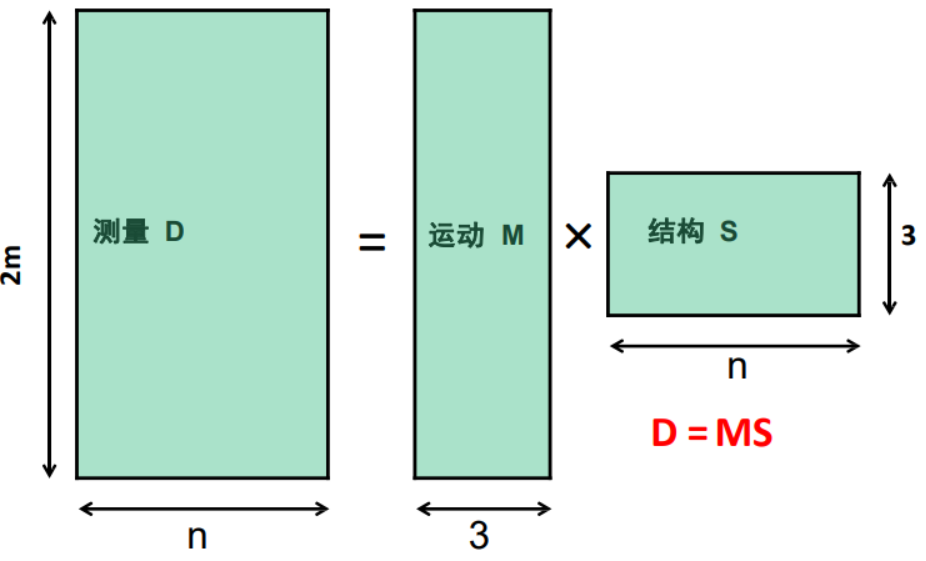
通過(guò)計(jì)算D的奇異值分解

由于\(rank(D) = 3\),理想情況下這里只有三個(gè)非零的奇異值\(\sigma_1,\sigma_2,\sigma_3\)
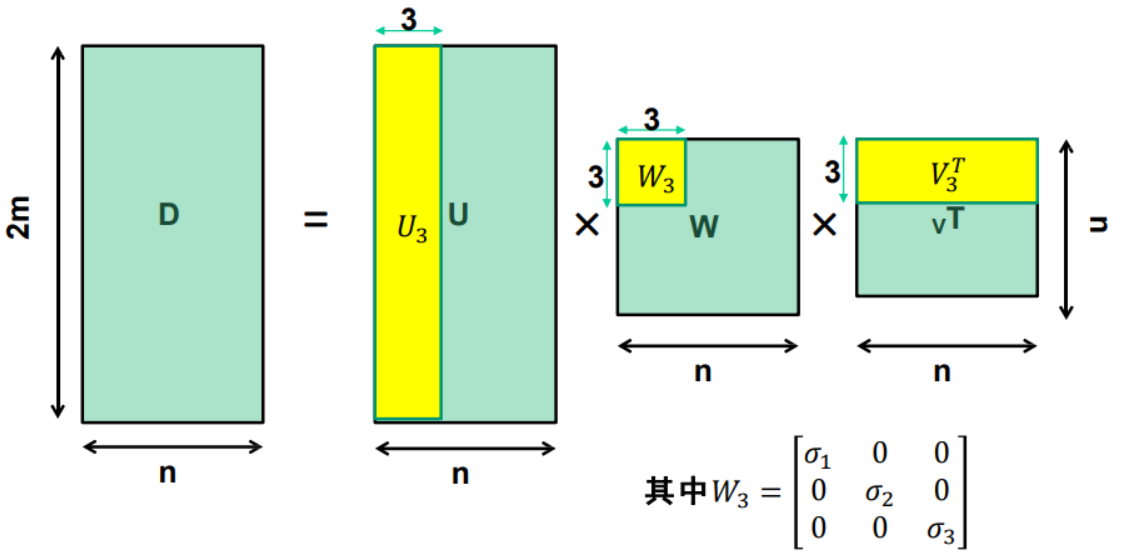
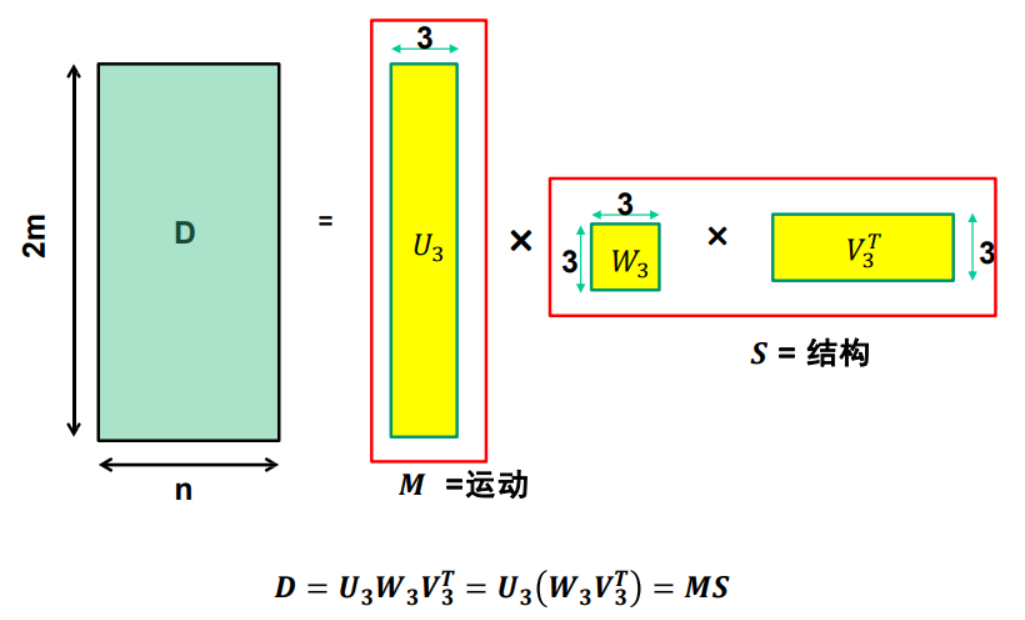
總結(jié):

問(wèn)題:這樣分解可以嗎?\(\longrightarrow\)可以。因此,解不是唯一的
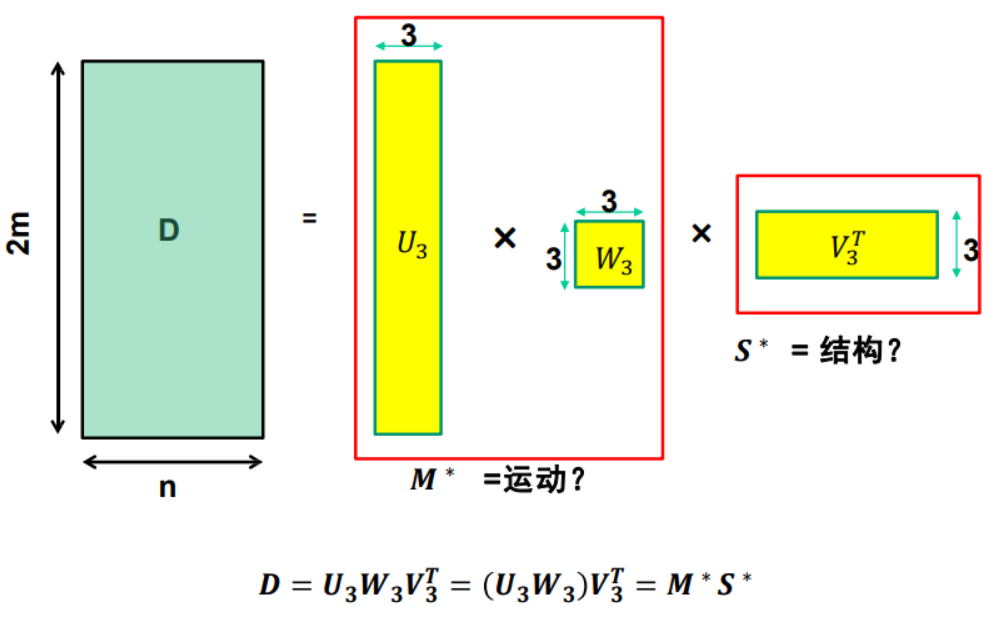
仿射結(jié)構(gòu)恢復(fù)歧義:
-
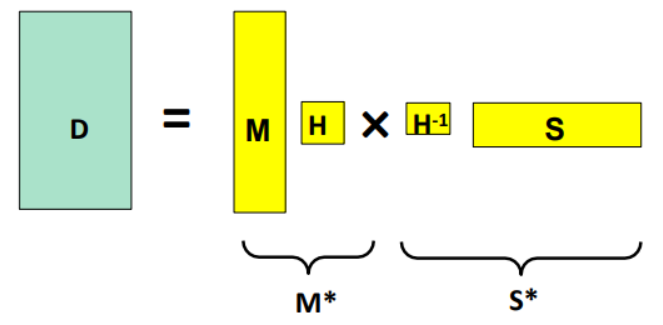
分解不唯一。通過(guò)以下變換可以得到相同的D:
\[M^* = MH\\ S^* = H^{-1}S \]其中\(H\)是任意可逆的\(3\times 3\)矩陣
-
必須利用其他約束條件來(lái)解決歧義
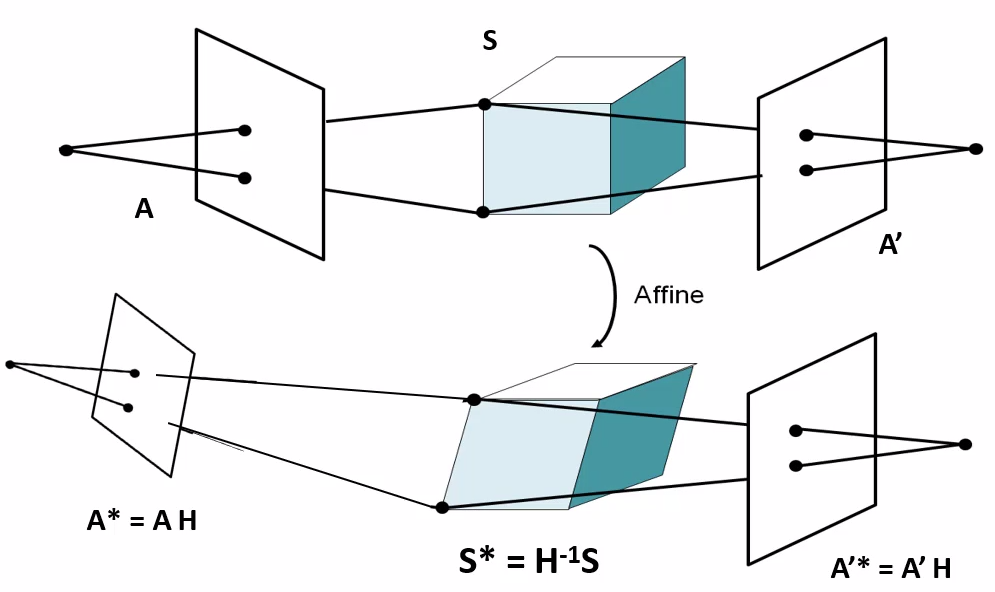

問(wèn)題:給定m個(gè)相機(jī),n個(gè)三維點(diǎn),可以有多少個(gè)等式\((2mn)\),多少個(gè)未知量\((3n+8m - 8)\)?
由于求不出真實(shí)解,與真實(shí)解總相差一個(gè)H矩陣\((3 \times 3)\),這個(gè)矩陣有8個(gè)自由度,所以真正有解的是\(3n + 8m - 8\),要把8減去
即需要約束 \(2 m n \ge 3n + 8m - 8\)
透視結(jié)構(gòu)恢復(fù)
問(wèn)題:已知n個(gè)三維點(diǎn)\(X_j(j = 1,...,n)\)在m張圖像中的對(duì)應(yīng)點(diǎn)的像素坐標(biāo)\(x_{ij}\),且\(x_{ij} = M_iX_j,(i = 1,...,m;j = 1,...,n)\)
? 其中,\(M_i\)為第\(i\)張圖片對(duì)應(yīng)的攝像機(jī)的投影矩陣
求解:
- n個(gè)三維點(diǎn)\(X_j(j=1,...,n)\)的坐標(biāo)
- m個(gè)攝像機(jī)投影矩陣\(M_i(i = 1,...,m)\)

以兩視圖為例:
式子乘一個(gè)\(H\)和\(H^{-1}\)得
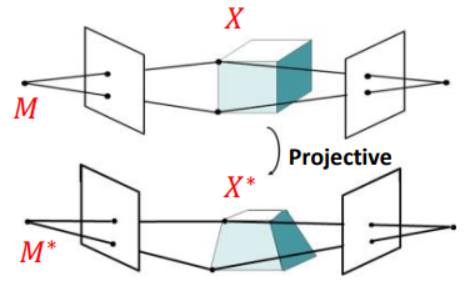
因此\(M、X\) 和 \(M^*、X^*\)都是\(x_{ij}=M_iX_j\)的解(透視結(jié)構(gòu)也有歧義性)
恢復(fù)方法:
在相差一個(gè)\(4\times 4\)的可逆變換的情況下恢復(fù)攝像機(jī)運(yùn)動(dòng)與場(chǎng)景結(jié)構(gòu)
- 代數(shù)方法(通過(guò)基礎(chǔ)矩陣)
- 因式分解法(通過(guò)SVD)
- 捆綁調(diào)整
代數(shù)方法
-
求解基礎(chǔ)矩陣F
歸一化八點(diǎn)法
-
利用F估計(jì)攝像機(jī)矩陣
\(F \longrightarrow M_1,M_2\)
-
三角化計(jì)算三維點(diǎn)坐標(biāo)
\(x_j^* = \mathop{argmin}\limits_{X_j}(d(x_{1j},M_1X_j) + d(x_{2j},M_2X_j))\)
利用F估計(jì)攝像機(jī)矩陣:
由于透視歧義的存在,我們總是可以找到一個(gè)可逆矩陣H,使得:

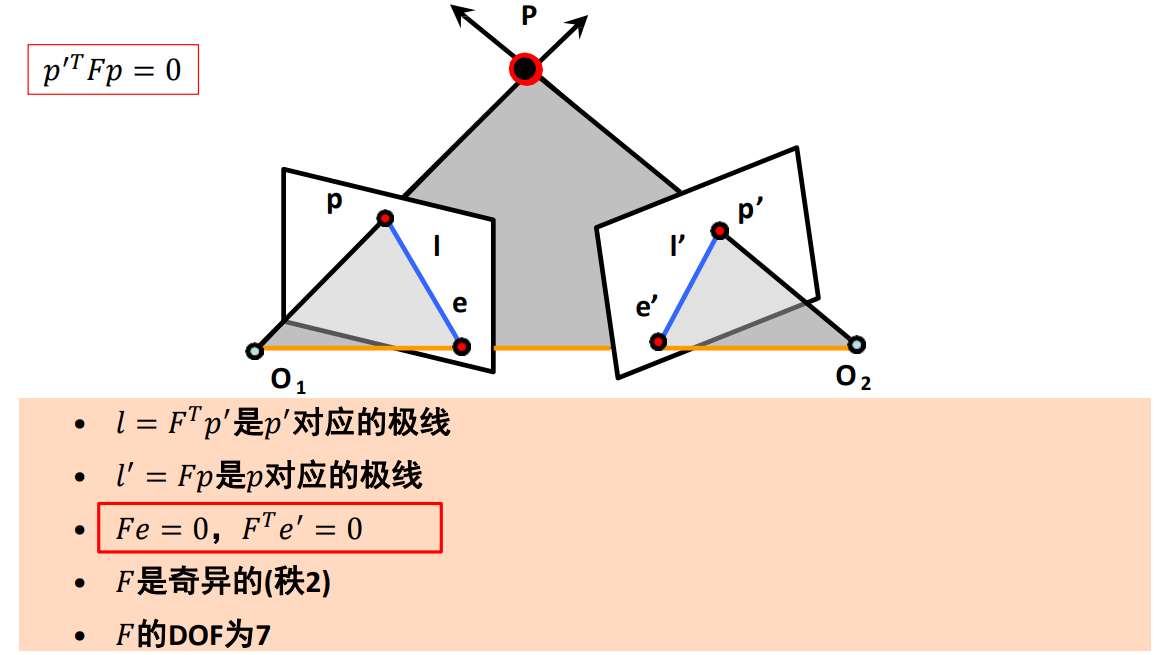
已知:\(x'Fx = 0 \qquad \qquad F = [b_{\times}]A\)
-
計(jì)算b :
-
考慮乘積\(F^T b\) \(F^{T}·b = ([b_{\times}]A)^T·b = A^T[b_{\times}]^T·b = -A^T[b_{\times}]·b = 0\) \(F^T b = 0\)
-
b為\(F^T\)矩陣最小奇異值的右奇異向量,且\(||b|| = 1\)
-
-
計(jì)算A:
-
定義:\(A' = -[b_{\times}]F\)
-
驗(yàn)證\([b_{\times}]A' = F\)
\[[b_{\times}]A' = -[b_{\times}][b_{\times}]F = - (bb^T-|b|^2I)F = -bb^TF + |b|^2F = 0 + 1·F = F \] -
因此,\(A = A' = -[b_{\times}]F\)
-
攝像機(jī)矩陣
那么,這里的b是什么呢?在極幾何約束中,有\(F^Te = 0\)這條性質(zhì),所以b是一個(gè)極點(diǎn)!
N視圖情況:
分別對(duì)每一個(gè)圖像對(duì)\(I_k\)和\(I_h\)計(jì)算運(yùn)動(dòng)與結(jié)構(gòu)
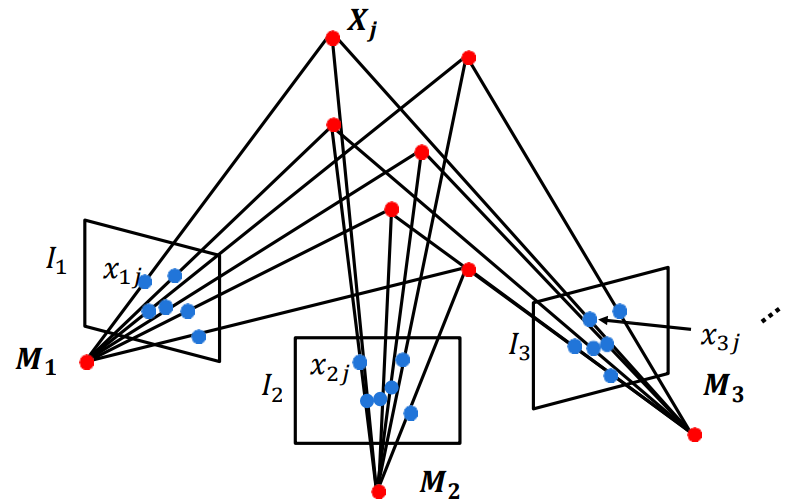
問(wèn)題:
但是通過(guò)兩兩的方法(從第三個(gè)轉(zhuǎn)到第二個(gè)再轉(zhuǎn)到第一個(gè))會(huì)有累計(jì)誤差!
捆綁調(diào)整(BA)
代數(shù)法與分解法的局限性:
-
因式分解法假定所有的點(diǎn)都是可見的,所有下述場(chǎng)合不可用:
- 存在遮擋
- 建立對(duì)應(yīng)點(diǎn)關(guān)系失敗
-
代數(shù)法應(yīng)用于2視圖重建
- 容易出現(xiàn)誤差累計(jì)
恢復(fù)結(jié)構(gòu)和運(yùn)動(dòng)的非線性方法
最小化重投影誤差:\(E(M,X) = \frac{1}{mn} \sum\limits_{i=1}^m \sum\limits_{j=1}^nD(X_{ij}, M_iX_j)^2\)
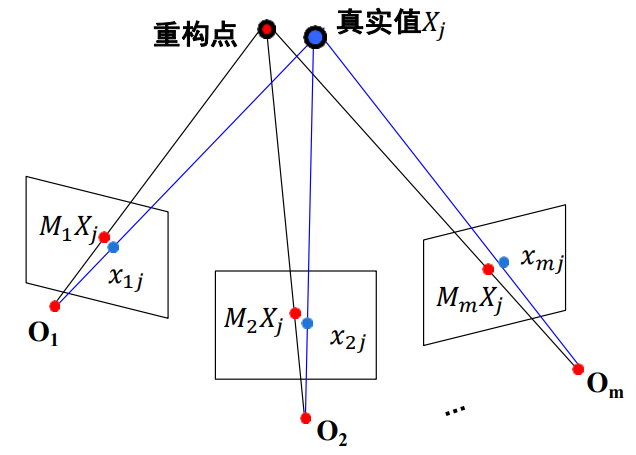
非線性最小化問(wèn)題:
牛頓法 與 L-M方法 求解
優(yōu)勢(shì):
- 同時(shí)處理大量視圖
- 處理丟失的數(shù)據(jù)
局限性:
- 大量參數(shù)的最小化問(wèn)題
- 需要良好的初始條件
實(shí)際操作:
- 常用于SFM的最后一步,分解或代數(shù)方法可作為優(yōu)化問(wèn)題的初始解


 浙公網(wǎng)安備 33010602011771號(hào)
浙公網(wǎng)安備 33010602011771號(hào)