淺談基環樹
淺談基環樹
定義
對于一個連通圖圖 \(G\),如果其點數與邊數相等,那我們便稱它為一個基環樹。
也就是說,在一棵樹上加一條邊,就形成了一棵基環樹。
一般地,如果圖 \(G\) 不連通,其點數與邊數相等,那么肯定就是若干個基環樹的組合,稱之為基環森林。
我們通常將基環樹分為以下幾類:
-
無向基環樹:基環樹由無向邊連接。

-
內向基環樹:基環樹由有向邊連接,每個節點出度都為 \(1\)。
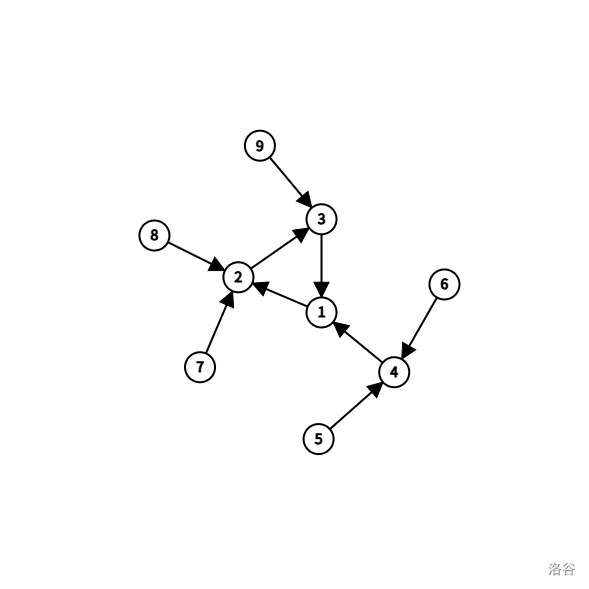
-
外向基環樹:基環樹由有向邊連接,每個節點入度都為 \(1\)。
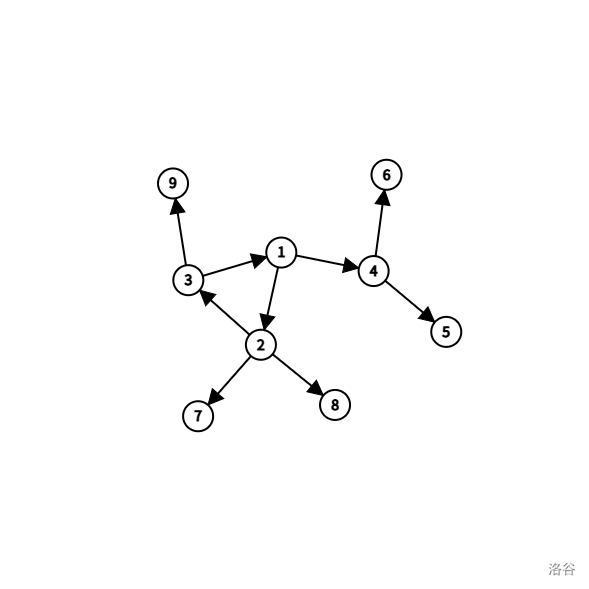
不同的基環樹,我們都有不同的處理方法,選對處理方法往往能夠事半功倍,具體會在下面例題中講到。
思路
對于一棵基環樹的問題,我們通常有以下兩種處理方法:
-
我們將一棵基環樹視為一個環上面掛了很多子樹,然后分別處理每一個子樹,將信息合并到在環上的根上,把一棵基環樹問題轉化為一個在環上的問題
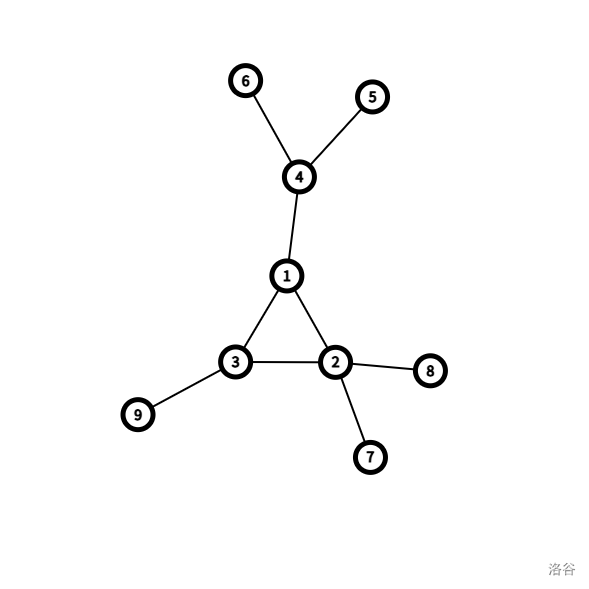
-
我們將一棵基環樹視為一個多了一條邊的樹,可以先將這一邊刪掉,將其轉化為樹上問題,之后我們再考慮加上這條邊造成的影響,將之前的結果加上影響即可
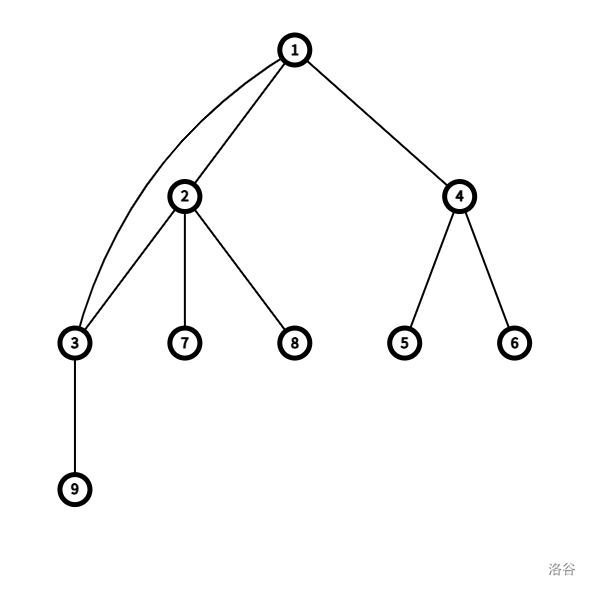
例題
P2607 [ZJOI2008] 騎士 link
題目大意
給出一個 \(n\)(\(1 \le n \le 10^6\))個點的帶點權的基環森林,求這個基環森林的最優獨立集。
最優獨立集:選出若干個點,使其兩兩之間沒有連邊,最大化這些點的點權和。
解題思路
我們將一個騎士和他痛恨的騎士連邊,由于兩者間只要選一個另一個就不能選,所以可以連無向邊,因此這就構成了一個無向基環森林。
對于每一棵基環樹,我們都求出它的最優獨立集,最后相加即可。
現在我們先考慮思路 2。
首先,我們需要找到這棵基環樹的環,將其上的一條邊斷掉,也就是說只需要求環上的一條邊即可。
無向基環樹找環需任選一點為根,進行 dfs,訪問過的點都進行標記,直到經過一條邊到達的點已經標記過,就說明這條邊在環上,記錄即可。
代碼實現上有很多點要注意,由于存在二元環的情況,即父子之間成環,也就是說父子之間有兩條邊,我們刪除環上一條邊后,仍然可以通過第二條邊到達父親。
這說明我們不能使用點判斷是否重復走,也就是不能使用 v != fa[v],因為這樣會導致 v 不能通過另一條邊到達 fa[v],所以需要通過邊來判斷,即走的這條邊是否和上一條邊相同。
具體地,我們使用鏈式向前星加邊時對應雙向邊的編號是相鄰的,這樣我們就令編號從 \(2\) 開始,使得邊 i 的對應邊即為 i ^ 1,再在 dfs 時記錄上一次經過的邊 pre,通過 (i ^ 1) != pre 判斷是否經過是否經過上一次經過的邊。(如果鏈式向前星一開始初始化為 \(0\) 就不能讓編號從 \(0\) 開始,因為 \(0\) 號會被認為是沒有邊)
同理,在之后的 dp 中,我們判斷是否經過刪除的那條邊時也不能用點判斷,要記錄刪除的邊的編號通過邊判斷。
這樣,記錄了刪除的邊之后,確保每次不經過這條邊,便可以開始樹形 dp:
- 狀態表示:\(dp_{i,0/1}\) 表示以 \(i\) 為根的子樹內,不選/選 \(i\) 號節點,其最大獨立集的大小。
- 初始化:\(dp_{i,0} = 0\),\(dp_{i,1} = a_i\)(\(a_i\) 為 \(i\) 的權值)
- 狀態轉移
- 不選 \(i\):則兒子無限制,即\[dp_{i,0} = \sum{\max(dp_{son,1},dp_{son,0})} \]
- 選 \(i\):則兒子都不能選,即\[dp_{i,1} = \sum{dp_{son,0}} \]
- 不選 \(i\):則兒子無限制,即
- 答案:\(\max(dp_{root, 0},dp_{root, 1})\)
最后考慮刪除的邊 \((u, v)\) 造成的影響。
刪除后,有可能兩者都選,不符合題意,因此我們要使其最多只選一個。
可以先欽定 \(u\) 不選,以 \(u\) 為根跑一遍 dp,再欽定 \(v\) 不選,以 \(v\) 為根跑一遍 dp,這使得至少有一個不選,最后我們合并兩者的答案,\(\max(dp_{u, 0}, dp_{v, 0})\) 即為答案。
另外,本題也可以使用思路 1,將每個子樹 dp 后再在環上 dp,但很顯然其實現難度大于思路 2,故不再贅述。
代碼實現
#include <bits/stdc++.h>
#define endl "\n"
#define ll long long
using namespace std;
const int N = 1e6 + 10;
struct edge
{
int to, next;
} e[N << 1];
int n, tot = 2, ui, vi, ei;
int h[N], a[N];
ll dp[N][2], ans;
bool vis[N];
void add(int u, int v)
{
e[tot].to = v;
e[tot].next = h[u];
h[u] = tot++;
}
void find_circle(int u, int pre)
{
vis[u] = 1;
for (int i = h[u]; i; i = e[i].next)
{
int v = e[i].to;
if ((i ^ 1) != pre)
{
if (vis[v])
{
ui = u, vi = v, ei = i | 1;
continue;
}
find_circle(v, i);
}
}
}
void dfs(int u, int pre)
{
dp[u][0] = 0, dp[u][1] = a[u];
for (int i = h[u]; i; i = e[i].next)
{
int v = e[i].to;
if ((i ^ 1) != pre && (i | 1) != ei)
{
dfs(v, i);
dp[u][0] += max(dp[v][0], dp[v][1]);
dp[u][1] += dp[v][0];
}
}
}
int main()
{
ios :: sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 1; i <= n; i++)
{
int v;
cin >> a[i] >> v;
add(i, v);
add(v, i);
}
for (int i = 1; i <= n; i++)
{
if (vis[i])
{
continue;
}
find_circle(i, -1);
dfs(ui, -1);
ll tmp = dp[ui][0];
dfs(vi, -1);
ans += max(tmp, dp[vi][0]);
}
cout << ans << endl;
return 0;
}
P4381 [IOI 2008] Island link
題目大意
給出一個 \(n\)(\(2 \le n \le 10^6\))個點的帶邊權的基環森林,求所有基環樹的直徑之和。
直徑:基環樹中距離最遠的兩點間的距離。
解題思路
一棵樹加上一條邊后,其直徑難以基于原來的直徑算出,因此我們考慮思路 1。
先分類討論,基環樹的直徑可以分為以下兩種情況:
- 直徑不經過環(環上的邊都不在直徑上):將所有的子樹的直徑求出取最大值即可。
- 直徑經過環(存在環上的邊在直徑上):設 \(u,v\) 為環上兩點,那么直徑一定能表示為 \(d_u + d_v + dis(u, v)\),其中 \(d_i\) 表示 \(i\) 子樹內離 \(i\) 最遠的點到 \(i\) 的距離(該子樹的最大深度),\(dis(u, v)\) 表示 \(u\) 和 \(v\) 在環上的距離。
我們主要是要解決出下面那種情況。
同樣是思路 1,一般有兩種實現方式:樹形 dp與拓撲排序,下面都會講解。
法 1
建雙向邊,構成一個無向基環森林。
同樣地,我們先找環,這一次我們需要求出具體的環,因為 \(dis(u,v)\) 是由若干條邊組成的,并且記錄邊我們擁有的信息更多,所以我們需要將所有的邊都記錄在數組中。
我們仍然采用 dfs,但由于要記錄每一條邊,實現會有些許不同。
- 我們記錄其 \(dfn\) 序以代替打標記,如果我們從 \(u\) 走到了一個已經訪問過的點 \(v\),還需判斷是否 \(dfn_v > dfn_u\),這保證了我們只允許從前輩訪問后輩的時候再記錄環,否則環會被記錄兩遍(后輩訪問前輩也會記錄一遍)。
- 我們預處理數組 \(pre_i\),表示 \(i\) 是他的父親由 \(pre_i\) 這條邊到達 \(i\) 的,這使得當前輩 \(u\) 經過一條邊到一個已經訪問過的后輩 \(v\) 時,只需讓 \(v\) 一直沿著 \(pre_i\) 走,邊走邊將 \(pre_i\) 放入數組,直到到達 \(u\) 就停止(特別地,我們可以將這條多出來的 \((u, v)\) 放在數組的 \(0\) 號)。
- 找環時還應將所有環上的點進行標記,避免 dp 時跑到環上的其他點。
找到環上的所有邊后,我們對這個環上的每個點,以其為根進行樹形 dp,求出 \(d_i\),順便處理分類討論的第一種情況,記第一種情況的最長直徑為 \(mx\),每次在更新 \(d_i\) 前,令 \(mx = \max(mx, d_i + d_{son} + w(i,son))\) 即可。
現在我們考慮處理這個環上問題,即對環上兩點 \(u,v\),求 \(\max(d_u + d_v + dis(u, v))\)。
可以破環成鏈復制一份后跑單調隊列 dp,但這里介紹一個更加簡單的方法。
我們仍然破環成鏈,記 \(s_i\) 為前 \(i\) 條邊的前綴和,\(l_i\)、\(r_i\) 為第 \(i\) 條邊的左端點和右端點,\(len\) 為環的長度。
那么最大值可以分為以下兩種情況:
由于我們是枚舉 \(i\) 的,可以將一些常值提出,也就是說我們只需預處理 \(\max(d_{l_j} - s_j)\)、\(\max(d_{l_j} - s_j)\) 加上即可以做到 \(O(n)\) 復雜度。
答案即為 \(\max(mx, res1, res2)\)。
法 2
我們只連單向邊,構成一個內向基環森林。
然后我們進行拓撲排序,將度為 \(0\) 的點放入隊列,之后就按拓撲排序的方式走,出隊后用自身信息更新父親節點,然后進行標記。
可以發現,只有環上的點不會進入隊列,也就是不會被標記,并且通過拓撲排序我們已經將子樹的信息都合并到的環上,最后我們只剩下了若干個環需要處理。
接著對每個環計算第二種情況的結果即可,法 1 中已經提到了。
可以看到,拓撲排序是一種很好的處理基環樹問題的方法,其碼量要小于前者。
代碼實現
法 1
#include <bits/stdc++.h>
#define endl "\n"
#define ll long long
using namespace std;
const int N = 1e6 + 10;
struct edge
{
int from, to, w, next;
} e[N << 1];
int n, tot = 2;
int h[N], pre[N];
int dfn[N], dfc;
bool vis[N];
int lp[N], cnt;
ll ans, mx, d[N], s[N];
void add(int u, int v, int w)
{
e[tot].from = u;
e[tot].to = v;
e[tot].w = w;
e[tot].next = h[u];
h[u] = tot++;
}
void find_circle(int u)
{
dfn[u] = ++dfc;
for (int i = h[u]; i; i = e[i].next)
{
int v = e[i].to;
if ((i ^ 1) == pre[v])
{
continue;
}
if (!dfn[v])
{
pre[v] = i;
find_circle(v);
continue;
}
if (dfn[v] < dfn[u])
{
continue;
}
vis[v] = 1;
lp[0] = i ^ 1;
while (v != u)
{
lp[++cnt] = pre[v];
vis[e[pre[v]].from] = 1;
v = e[pre[v]].from;
}
}
}
void dfs(int u)
{
vis[u] = 1;
for (int i = h[u]; i; i = e[i].next)
{
int v = e[i].to, w = e[i].w;
if (!vis[v])
{
dfs(v);
mx = max(mx, d[u] + d[v] + w);
d[u] = max(d[u], d[v] + w);
}
}
}
ll solve(int x)
{
mx = dfc = cnt = 0;
find_circle(x);
dfs(e[lp[0]].from);
ll len = e[lp[0]].w;
for (int i = 1; i <= cnt; i++)
{
dfs(e[lp[i]].from);
s[i] = s[i - 1] + e[lp[i]].w;
}
len += s[cnt];
ll res1 = -1e18, res2 = -1e18, mx1 = -1e18, mx2 = -1e18;
for (int i = 1; i <= cnt; i++)
{
mx1 = max(mx1, d[e[lp[i]].to] - s[i - 1]);
mx2 = max(mx2, d[e[lp[i]].to] + s[i - 1]);
res1 = max(res1, mx1 + d[e[lp[i]].from] + s[i]);
res2 = max(res2, mx2 + d[e[lp[i]].from] - s[i]);
}
return max(mx, max(res1, res2 + len));
}
int main()
{
ios :: sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 1; i <= n; i++)
{
int v, w;
cin >> v >> w;
add(i, v, w);
add(v, i, w);
}
for (int i = 1; i <= n; i++)
{
if (!vis[i])
{
ans += solve(i);
}
}
cout << ans << endl;
return 0;
}
法 2
#include <bits/stdc++.h>
#define endl "\n"
#define ll long long
using namespace std;
const int N = 1e6 + 10;
int n;
int fa[N], w[N], deg[N];
queue<int> q;
ll d[N], dp[N], ans;
void topo()
{
for (int i = 1; i <= n; i++)
{
if (!deg[i])
{
q.push(i);
}
}
while (!q.empty())
{
int x = q.front();
q.pop();
dp[fa[x]] = max(dp[fa[x]], max(dp[x], d[fa[x]] + d[x] + w[x]));
d[fa[x]] = max(d[fa[x]], d[x] + w[x]);
if (!(--deg[fa[x]]))
{
q.push(fa[x]);
}
}
}
ll solve(int x)
{
ll len = w[x], res1 = dp[x], res2 = -1e18, mx1 = d[x], mx2 = d[x];
int st = x;
deg[x] = 0;
x = fa[x];
while (x != st)
{
deg[x] = 0;
res1 = max(res1, max(dp[x], d[x] + len + mx1));
res2 = max(res2, d[x] - len + mx2);
mx1 = max(mx1, d[x] - len);
mx2 = max(mx2, d[x] + len);
len += w[x];
x = fa[x];
}
return max(res1, res2 + len);
}
int main()
{
ios :: sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> fa[i] >> w[i];
deg[fa[i]]++;
}
topo();
for (int i = 1; i <= n; i++)
{
if (deg[i])
{
ans += solve(i);
}
}
cout << ans << endl;
return 0;
}
P3472 [POI 2008] MAF-Mafia link
題目大意
有 \(n\)(\(1 \le n \le 10 ^ 6\))個人,每個人都用槍指著一個人(可以是自己),給出每個人用槍指著的人,之后按照需按照一定順序開槍,求可能的最小和最大的死亡人數。
解題思路
每個人與他指著的人建單向邊,形成一個內向基環森林。
由于思路 1 并不能很好地解釋,我們仍然采取思路 2 的觀點,即把基環樹看作掛著許多子樹的環。
我們先分析最大值,考慮一個環,最少只有一個人活下來(特別地,自環的話是可以全部死亡,需要特判)。
我們再考慮一棵樹,葉子節點一定不死,因為沒有人指著他們,然后如果想要更多人死,那就要盡可能在一個人死之前就開槍,于是我們可以從根的兒子先開始開槍,然后一層一層地開槍,最后只有葉子會活下來。
那么,結合兩種觀點,如果這個環上有子樹的話,先讓環開槍,最后只讓這個有子樹的點活下來,最后讓所有子樹按照層數開槍,環上的那個點會死掉,其他不是葉子的也會死,也就是這棵子樹只有葉子活下來。
所以,最大值可以分三種情況:
- 自環:沒人活。
- 環:活一個。
- 基環樹:葉子活下來。
所有基環樹存活數加起來,就能求得最小存活數,也就是最大死亡數。
我們再來分析最小值,根據上面的分析可以知道,葉子節點一定活下來。
遞推可知,葉子節點的父親必死,那么葉子節點的爺爺如果沒有其他葉子指著就能活下來,然后一層層推廣開來。
我們使用貪心思想,如果一個點是必死的,那我們絕對不讓他在死前開槍,這一定是不優的,因為這個人的死亡最多能使其指向的點從死轉到活,并不能使兩個及以上的點由死到活以達到更優。
于是,我們可以發現活與死的等價條件:
- 活等價于是葉子或者指向他的點都死亡。
- 死等價于有活的點指向他。
基于這兩個條件,我們可以采用遞推的思想,一開始葉子的狀態一定是確定的,然后讓葉子去更新葉子父親,葉子父親去更新葉子爺爺,以此類推。
實現我們可以采取類似于拓撲排序的操作,先將度為 \(0\) 的點也就是葉子入隊,然后每次次取出隊首,更新其指向點的信息:
- 隊首狀態是死:將其指向的點的入度減 \(1\),如果其指向點入度為 \(0\),就將其標記為活,入隊。
- 隊首狀態是活:如果他指向的點狀態不是死,也就是說他還沒被打死,就將其標記為死,同時更新最小死亡數,入隊(我們不去修改它的度數,因為這使得其度數絕對不會被減到 \(0\),避免前面將其起死回生的情況)。
如此以來,最后還可能有一些狀態沒有確定的點,這些點只有可能是其中任何一個點都沒有被標記必死的環(如果一個環有點被其兒子標上必死,那么這個環就被打開了一個缺口,最后整個基環樹的狀態都能被確定)。
所以,我們再遍歷所有點,如果這個點狀態沒有確定,就一直往其指著的點走,遍歷這個環,并且都標記其狀態,最后找出次環的長度,對于一個環,其最大存活數顯然為 \(\frac{len}{2}\),加上即可。
代碼實現上,最小值可以和最大值一起處理,只需在進行拓撲排序時記錄一個 \(vis\) 表示此環有沒有環外的子樹,最后在遍歷環時將所有 \(vis\) 取或,為 \(0\) 就說明此環沒有子樹,需要將最大死亡數減 \(1\)。
代碼實現
#include <bits/stdc++.h>
#define endl "\n"
using namespace std;
const int N = 1e6 + 10;
int n, cnt;
int p[N], deg[N], st[N];
int ans1, ans2;
bool vis[N];
queue<int> q;
int main()
{
ios :: sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
ans1 = ans2 = n;
for (int i = 1; i <= n; i++)
{
cin >> p[i];
deg[p[i]]++;
}
for (int i = 1; i <= n; i++)
{
if (!deg[i])
{
ans1--, ans2--;
st[i] = 1;
vis[i] = 1;
q.push(i);
}
}
while (!q.empty())
{
int x = q.front();
q.pop();
vis[p[x]] = 1;
if (st[x] == 1)
{
if (st[p[x]] == 2)
{
continue;
}
st[p[x]] = 2;
q.push(p[x]);
}
else
{
if (--deg[p[x]])
{
continue;
}
st[p[x]] = 1;
q.push(p[x]);
ans1--;
}
}
for (int i = 1; i <= n; i++)
{
if (!st[i])
{
int len = 0;
bool flag = 0;
for (int j = i; !st[j]; j = p[j])
{
len++;
flag |= vis[j];
st[j] = 1;
}
ans1 -= len / 2;
ans2 -= (flag ^ 1) && (len != 1);
}
}
cout << ans1 << " " << ans2 << endl;
return 0;
}
P10933 創世紀 link
題目大意
給出一個有向基環森林,選出若干點,要求所有選出的點都必須要有一個沒被選出的點指向它,最大化選出點數。
解題思路
同樣地,這道題也可以考慮思路 1,但是思路 2 還是更加簡便。
這道題連邊上有些文章可作,我們將集成內向基環樹與外向基環樹的優點,進行連邊。
具體地,記 \(u\) 指向 \(v\),我們用數組 \(p\) 記錄一個點指向的點即 \(p_u = v\),這是內向基環樹;我們再用鏈式向前星由 \(v\) 向 \(u\) 建單向邊,這是外向基環樹。
這么連邊的好處是操作方便,內向基環樹優點是找環方便,由于點都是向內指的,只需隨便選一個點一直往其指向的點走,直到重復為止便找到了環;而鏈式向前星建單向邊的好處是方便 dp,刪去環上一邊后,以斷點為根,每個節點其連邊都是兒子。
上面已經說過了找環方法,將邊斷掉之后便可以開始樹形 dp:
- 狀態表示:\(dp_{i,0/1}\) 表示在以 \(i\) 根的子樹內,\(i\) 不選 / 選時的最大選點數。
- 初始化:\(dp_{i,0/1}=0\)
- 狀態轉移
-
不選 \(i\):則其子節點不受限制,即
\[dp_{i,0}=\sum_{j \in son_i}{\max(dp_{j,0},dp_{j,1})} \] -
選 \(i\):則其子節點至少有一個不選,即
\[dp_{i,1}=1+\max_{j \in son_i}{(dp_{j,0}+\sum_{k \in son_i,k \neq j}{\max(dp_{k,0},dp_{k,1})})} \]復雜度較高,考慮優化,發現右邊的和式與 \(dp_{i,0}\) 很相似,于是有:
\[\begin{aligned}dp_{i,1} &= 1+\max_{j \in son_i}{(dp_{j,0}+dp_{i,0} - \max(dp_{j,0},dp_{j,1}))} \\ &= 1 + dp_{i,0} - \min_{j \in son_i}{(\max(dp_{j,0},dp_{j,1}) - dp_{j,0})}\end{aligned} \]即可快速轉移。
-
- 答案:\(\max(dp_{rt,0},dp_{rt,1})\)
現在我們考慮刪去邊的影響,原來有一條邊是由根指向一個節點的,但是被刪除了,這意味者原來根是可以限制此節點的,現在不行了,也就是說我們要考慮根限制此節點的情況。
于是我們再跑一遍 dp,欽定選根節點,即這個點已經被限制住了,意味著就算選這個點其兒子也不受任何限制,只需將選這個點的 dp 值加上 \(\min_{j \in son_i}{(\max(dp_{j,0},dp_{j,1}) - dp_{j,0})}\) 即可,最后答案為 \(dp_{rt,1}\),與上面得到答案取最大值便得到了最終答案。
代碼實現
#include <bits/stdc++.h>
#define endl "\n"
using namespace std;
const int N = 1e6 + 10;
struct edge
{
int to, next;
} e[N];
int n, tot, rt, ans;
int a[N], h[N];
int dp[N][2];
bool vis[N];
void add(int u, int v)
{
tot++;
e[tot].to = v;
e[tot].next = h[u];
h[u] = tot;
}
void dfs(int u, bool flag)
{
dp[u][0] = 0;
vis[u] = 1;
int mn = 1e9;
for (int i = h[u]; i; i = e[i].next)
{
int v = e[i].to;
if (v != rt)
{
dfs(v, flag);
dp[u][0] += max(dp[v][0], dp[v][1]);
mn = min(mn, max(dp[v][0], dp[v][1]) - dp[v][0]);
}
}
dp[u][1] = 1 + dp[u][0] - mn;
if (flag && u == a[rt])
{
dp[u][1] += mn;
}
}
int main()
{
ios :: sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
add(a[i], i);
}
for (int i = 1; i <= n; i++)
{
if (!vis[i])
{
for (rt = i; !vis[rt]; rt = a[rt])
{
vis[rt] = 1;
}
dfs(rt, 0);
int tmp = max(dp[rt][0], dp[rt][1]);
dfs(rt, 1);
ans += max(tmp, dp[rt][0]);
}
}
cout << ans << endl;
return 0;
}


 浙公網安備 33010602011771號
浙公網安備 33010602011771號