注意，我們這里舉列的原碼和反碼只是為了求負數的補碼，在計算機中沒有原碼，反碼的存在，只有補碼。

一.原碼

1>.正數的原碼就是它的本身

　　假設使用一個字節存儲整數，整數10的原碼是：0000 1010

2>.負數用最高位是1表示負數

　　假設使用一個字節存儲整數，整數-10的原碼是：1000 1010

二.反碼

1>.正數的反碼跟原碼一樣

　　假設使用一個字節存儲整數，整數10的反碼是：0000 1010

2>.負數的反碼是負數的原碼按位取反（0變1,1變0），符號位不變

　　假設使用一個字節存儲整數，整數-10的反碼是：1111 0101

三.補碼（再次強調，整數的補碼才是在計算機中的存儲形式。）

1>.正數的補碼和原碼一樣

　　假設使用一個字節存儲整數，整數10的補碼是：0000 1010（第三次強調：這一串是10這個整數在計算機中存儲形式）

2>.負數的補碼是負數的反碼加1

　　假設使用一個字節存儲整數，整數-10的補碼是：1111 0110（第三次強調：這一串是-10這個整數在計算機中存儲形式）

四.在計算機中，為什么不用原碼和反碼，而是用補碼呢？

　　因為在使用原碼，反碼在計算時不準確，使用補碼計算時才準確。

1>.使用原碼計算10-10

　　　　     0000 1010　　（10的原碼）

　  　+        1000 1010 　　（-10的原碼）

------------------------------------------------------------

　　　　     1001 0100　　（結果為：-20，很顯然按照原碼計算答案是否定的。）

2>.使用反碼計算10-10

　　　　　　0000 1010　　（10的反碼）

　　　　+　  1111 0101　　（-10的反碼）

------------------------------------------------------------

　　　　　　1111 1111　　（計算的結果為反碼，我們轉換為原碼的結果為：1000 0000，最終的結果為：-0，很顯然按照反碼計算答案也是否定的。）

3>.使用補碼計算10-10

　　　　　　0000 1010　　（10的補碼）

　　　+　　 1111  0110　　（-10的補碼）

------------------------------------------------------------

　　　　  1 0000 0000　　（由于我們這里使用了的1個字節存儲，因此只能存儲8位，最高位（第九位）那個1沒有地方存，就被丟棄了。因此，結果為：0）

五.小試牛刀

　　有了上面的案例，接下來，我們來做幾個小練習吧，分別計算以下補碼表示的十進制數字是多少呢？

1>.0b0000 1111

　　相信這個數字大家異口同聲的就能說出它的答案是：15（因為正數的補碼和原碼一樣）

2>.0b1111 1111

　　計算過程：0b1111 1111（補碼）------>0b1111 1110（反碼）------>0b1000 0001（原碼）

　　將其換算成原碼之后就可以得到最后的結果為：-1

3>.0b1111 0000

　　計算過程：0b1111 0000（補碼）------>0b1110 1111（反碼）------>0b10010000(原碼)

　　將其換算成原碼之后就可以得到最后的結果為：-16

4>.0b1000 0001

　　計算過程：0b1000 0001（補碼）------>0b1000 0000（反碼）------->0b1111 1111（原碼）

　　將其換算成原碼之后就可以得到最后的結果為：-127

------------------------------------------------------------------------------------------------------------------------------------------

最近在tcp的基礎上寫一個自定義的協議，處理拆包粘包的時候發現一個情況

數據是以字節流的形式在tcp中傳輸，所以，大于一個字節的數據類型，都要轉為byte[] 的形式

以int類型舉例，在java中一個int類型的數據占4個字節，也就是需要new byte[4]

        int a = 9071;
        byte[] bytes = new byte[4];
        bytes[0] = (byte) (a >> 24 ); //  拿到最高位的8位
        bytes[1] = (byte) (a >> 16 );
        bytes[2] = (byte) (a >> 8 );
        bytes[3] = (byte) (a);

java中的數據類型都是有符號類型，也就是說區分正負的

一個字節=8bit，也就是說一個 byte 可以存放8個 0 或者 1

1 的二進制原碼是 0 000 000 1
-1 的二進制原碼是 1 000 000 1，補碼是 1111 1111

二進制的最高位為符號位，所以byte 的取值范圍為-128~127，（-2^7~2^7-1）

在 Java 中，是采用補碼來表示數據的。

正數的補碼和原碼相同，負數的補碼是在原碼的基礎上各位取反然后加 1。

譬如：int a = -29 的二進制表示為11111111111111111111111111100011

int 32字節，先取a的的絕對值求原碼，29 的原碼為00011101

不足4字節，高位補24個0

00000000000000000000000000011101

再求反碼

11111111111111111111111111100010

+1
于是得到了-29的二級制補碼

11111111111111111111111111100011

通過上面的代碼看，int 在tcp傳輸的時候要轉換為byte[], int a = -29; 一共4個字節32位，于是byte[4] 每一個小標存儲一個字節也就是8位，寫到這里我們發現還是用不上&0xff，不要著急，接下來就用上了

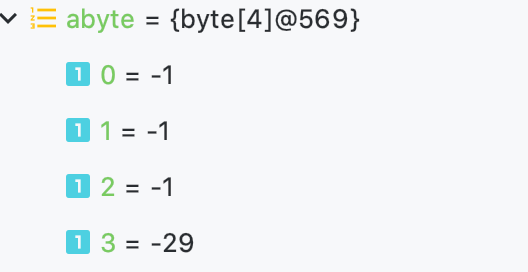
于是，我們發現int 29 被裝進 byte[] 的時候，成了這個樣子：

下標0表示的是前8位，
下標1表示的是8-16位，
下標2表示的是16-24位，
下標3表示的是24-32位

也很容易理解，因為-1的補碼就是 11111111 ，所以這4個byte的二進制組合起來就是int -29 的二進制

你把數據拆開了還要把它組合起來啊，也就是byte[] 轉 int

分解問題就是單個byte 轉 int

byte 八個bit位，int 32個bit位，byte為負數的時候，需要把高24位的全部置為0.保持低八位的一致性，不然得到的int就成了另一個數字

0xff 是16進制，也就是255 二進制也就是 1111 1111
補到32位也就是 這里是24個0 這里是八個1
一個負數的byte & 0xff的時候，高24位就成了0，保證了一致性
然而正數的補碼還是它自己，不受影響，雖然只有負數的時候才需要 &0xff，但不至于再判斷一次去吧？

 　　　　 byte a = -1;// 1111 1111
        short b = -1;//1111 1111 1111 1111
        int c = -1;//  1111 1111 1111 1111 1111 1111 1111 1111
        System.out.println(a);//-1
        System.out.println(b);//-1
        System.out.println(c);//-1

        System.out.println(a&0xff);// 1111 1111&1111 1111  =255
        System.out.println(a&0xffff);//(byte –> int 就是由8位變 16 位 高8位全部補1，如果是正數補0) 1111 1111 1111 1111&1111 1111 1111 1111  =65535
        System.out.println(a&0xffffffffL);//(byte –> int 就是由8位變 32 位 高24位全部補1，如果是正數補0)
        // 1111 1111 1111 1111 1111 1111 1111 1111&1111 1111 1111 1111 1111 1111 1111 1111  =4294967295

        System.out.println(b&0xff);//255
        System.out.println(b&0xffff);//65535
        System.out.println(b&0xffffffffL);//4294967295

        System.out.println(c&0xff);//255
        System.out.println(c&0xffff);//65535
        System.out.println(c&0xffffffffL);//4294967295