Paper Reading: TabNet: Attentive Interpretable Tabular Learning
Paper Reading 是從個人角度進行的一些總結分享,受到個人關注點的側重和實力所限,可能有理解不到位的地方。具體的細節還需要以原文的內容為準,博客中的圖表若未另外說明則均來自原文。
| 論文概況 | 詳細 |
|---|---|
| 標題 | 《TabNet: Attentive Interpretable Tabular Learning》 |
| 作者 | Sercan O. Ar?k, Tomas Pfister |
| 發表會議 | The Thirty-Fifth AAAI Conference on Artificial Intelligence (AAAI-21) |
| 會議年份 | 2021 |
| 論文代碼 | https://github.com/google-research/google-research/tree/master/tabnet |
作者單位:
Google Cloud AI Sunnyvale, CA
研究動機
深度學習在圖像、文本和音頻等領域取得了顯著成功,這很大程度上得益于標準架構,這些架構能高效地將原始數據編碼為有意義的表征。然而,現實世界 AI 應用中最常見的表格數據卻尚未出現這樣一個獲得廣泛成功的標準深度學習架構,目前絕大多數表格數據學習任務仍由基于集成決策樹的變體所主導。基于決策樹的算法在表格數據上表現出色,主要得益于以下幾點:
- 表征效率:對于表格數據中常見的、近似超平面邊界的決策流形,決策樹具有很高的表征效率;
- 可解釋性:決策樹的基本形式本身易于解釋,而其集成形式也有流行的事后解釋方法(如 SHAP);
- 訓練速度快:與復雜的深度學習模型相比,決策樹通常訓練速度更快。
先前提出的深度學習架構并不適合表格數據,它們通常嚴重過參數化,并且缺乏適合表格數據的歸納偏置,這常常導致它們無法為表格決策流形找到最優解。盡管面臨挑戰,但是深度學習的潛力遠超當前主導方法。對于大規模數據集,深度學習模型有望帶來顯著的性能提升,這符合模型性能隨數據量增加而提升的普遍規律。與樹學習相比,深度學習架構具有多重不可替代的優勢:
- 多模態數據高效編碼:可以整合并高效編碼圖像等多種數據類型與表格數據;
- 減少特征工程:可以減輕目前基于樹的方法中對特征工程的高度依賴;
- 適應流式數據:更易于從數據流中持續學習;
- 支持表征學習:端到端模型允許進行表征學習,從而支持許多有價值的應用場景。
文章貢獻
本文提出了一種用于表格數據深度學習的架構 TabNet,該模型的核心創新在于模仿決策樹的特征選擇能力,通過一種序列注意力機制(sequential attention) 來實現實例級的軟特征選擇。在每一步決策中,TabNet 都會動態地、稀疏地選擇最相關的特征子集進行推理,從而將模型的學習能力集中在最顯著的特征上。這不僅提高了學習效率,減少了冗余參數,還自然地為模型提供了內在的可解釋性。其編碼器由多個決策步驟組成,每個步驟包含一個用于特征選擇的注意力變換器(Attentive Transformer) 和一個用于特征處理的特征變換器(Feature Transformer)。此外,TabNet 首次為表格數據引入了掩碼自監督學習框架,通過預測被掩碼的特征來進行預訓練,從而能夠有效利用大量未標注數據來提升模型在下游任務中的性能。通過廣泛的實驗驗證,證明了TabNet 在多個不同領域的分類和回歸數據集上達到或超越了當前主流表格學習模型的性能,同時提供了局部和全局兩個層面的可解釋性。
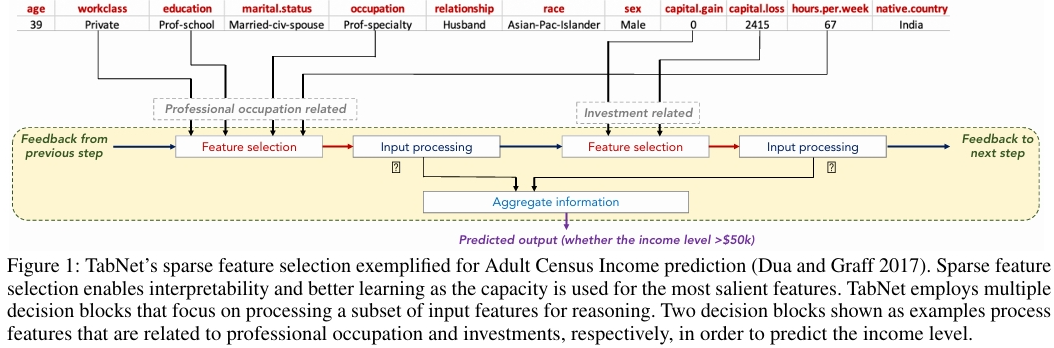
預備知識
Sparsemax
Sparsemax 是一個激活函數,是傳統 Softmax 函數的一種替代方案。與 Softmax 總是產生一個稠密的概率分布(所有輸出都大于零)不同,Sparsemax 能夠產生一個稀疏的概率分布,即對于某些輸入 Sparsemax 的輸出會精確地為 0。
可以將 Sparsemax 理解為一個在概率單純形上的歐幾里得投影,目標為給定一個分數向量 $ \mathbf{z} = [z_1, z_2, ..., z_K] $,我們希望將其轉換為一個概率分布 \(\mathbf{p} = [p_1, p_2, ..., p_K]\),其中 \(\sum_{i=1}^K p_i = 1\) 且 \(p_i \ge 0\)。Softmax 的做法是通過指數函數進行非線性變換,這保證了所有輸出都大于零,但永遠不會等于零。Sparsemax 的做法是尋找一個概率分布 \(\mathbf{p}\),使得 \(\mathbf{p}\) 與原始分數 \(\mathbf{z}\) 的歐幾里得距離最小,同時滿足概率分布的約束條件。這個“投影”操作將一部分較低的分數直接“截斷”為 0,而剩余的概率質量則均勻地分配給那些“被選中”的維度。Sparsemax 函數的定義如下,其中 \(\Delta^{K-1}\) 是 \(K-1\) 維的概率單純形,即滿足 \(\sum_{i=1}^K p_i = 1\) 且 \(p_i \ge 0\) 的所有點的集合。
Sparsemax 的輸出可以按以下步驟計算:
- 排序:將輸入向量 \(\mathbf{z}\) 按從大到小的順序排序。令 \(z_{(1)} \ge z_{(2)} \ge \cdots \ge z_{(K)}\) 表示排序后的值。
- 尋找支持集:找到支持集的大小 \(\kappa(\mathbf{z})\),即輸出中非零元素的最大個數。它被定義為滿足下式的最大 \(k\):\[\kappa(\mathbf{z}) = \max \left\{ k \in [1, K] \ \middle|\ 1 + k z_{(k)} > \sum_{j \le k} z_{(j)} \right\} \]一個更常見的等價計算方法是找到閾值函數 \(\tau(\mathbf{z})\),即需要找到最大的 \(k\),使得 \(z_{(k)} > \tau(\mathbf{z})\),這個 \(\tau\) 就是最終的閾值。\[\tau(\mathbf{z}) = \frac{\left(\sum_{j=1}^k z_{(j)}\right) - 1}{k} \]
- 計算閾值:根據找到的 \(k\) 計算閾值:\[\tau(\mathbf{z}) = \frac{\left(\sum_{j=1}^{\kappa(\mathbf{z})} z_{(j)}\right) - 1}{\kappa(\mathbf{z})} \]
- 輸出結果:Sparsemax 的最終輸出是輸入分數減去閾值 \(\tau\),然后進行裁剪(ReLU 操作):\[\text{Sparsemax}(\mathbf{z})_i = \max(z_i - \tau(\mathbf{z}), 0) \]
給出一個簡單的例子,假設有一個輸入向量 \(\mathbf{z} = [1.0, 0.8, 0.2, -0.5]\):
- 排序:\(z_{(1)} = 1.0, \ z_{(2)} = 0.8, \ z_{(3)} = 0.2, \ z_{(4)} = -0.5\)。
- 尋找 \(k\):
- 測試 \(k=1\): \(\tau = (1.0 - 1)/1 = 0\)。\(z_{(1)}=1.0 > 0\),成立。
- 測試 \(k=2\): \(\tau = ((1.0+0.8) - 1)/2 = 0.8/2 = 0.4\)。\(z_{(2)}=0.8 > 0.4\),成立。
- 測試 \(k=3\): \(\tau = ((1.0+0.8+0.2) - 1)/3 = (2.0 - 1)/3 \approx 0.333\)。\(z_{(3)}=0.2 < 0.333\),不成立。
- 所以 \(\kappa(\mathbf{z}) = 2\)。
- 計算閾值:\(\tau = 0.4\)(由上一步 \(k=2\) 時已算出)。
- 輸出:對每個 \(z_i\) 減去閾值 0.4 并裁剪。
- \(p_1 = \max(1.0 - 0.4, 0) = 0.6\)
- \(p_2 = \max(0.8 - 0.4, 0) = 0.4\)
- \(p_3 = \max(0.2 - 0.4, 0) = 0\)
- \(p_4 = \max(-0.5 - 0.4, 0) = 0\)
最終,\(\text{Sparsemax}(\mathbf{z}) = [0.6, 0.4, 0.0, 0.0]\)。可以看到,兩個較小的分數被精確地置為了零,結果是一個稀疏分布。
門控線性單元
GLU(Gated Linear Unit,門控線性單元) 函數的核心思想來源于門控機制,類似于 LSTM 或 GRU 中的門控單元。它的目的是通過一個“門”來控制信息的流動,讓模型能夠學會在網絡的每一層中保留哪些信息以及舍棄哪些信息。GLU 的操作是給定一個輸入張量 \(X\),通常張量的最后一個維度(即特征維度)是偶數。首先將其均勻地分割為兩部分 $ A, B = \text{split}(X, \text{axis}=-1) $,它們的形狀完全相同。然后,GLU 的計算如下:
其符號的含義為:
| 符號 | 含義 |
|---|---|
| $ A $ | “信息”部分 |
| $ B $ | “門”部分 |
| $ \sigma $ | Sigmoid 函數,它將 $ B $ 中的每個元素的值壓縮到 (0, 1) 區間 |
| $ \otimes $ | 逐元素乘法 |
Sigmoid 函數產生的門控值 \(\sigma(B)\) 就像一個“水龍頭”或“閥門”,模型通過訓練來學習如何生成最合適的門控信號 $ B $,以優化最終任務。
- 當門控值接近 1 時,對應位置的信息 \(A\) 幾乎被完全保留。
- 當門控值接近 0 時,對應位置的信息 \(A\) 幾乎被完全屏蔽。
一個簡單的計算示例如下,假設我們有一個特征維度為 4 的輸入向量 \(X = [1, 2, 3, 4]\),首先分割將其均勻分割為信息部分 $ A = [1, 2] $ 和門控部分 $ B = [3, 4] $。接著計算門控信號,將 $ B $ 輸入 Sigmoid 函數得 \(\sigma(B) \approx [0.9526, 0.9820]\)。然后進行逐元素相乘:$ \text{GLU}(X) = A \otimes \sigma(B) = [1 * 0.9526, 2 * 0.9820] \approx [0.9526, 1.9640] $,可以看到,原始信息 $ A = [1, 2] $ 被門控信號縮放為了 $ [0.9526, 1.9640] $。
原始的 GLU 被進行了多種改進,產生了不同的激活函數,它們的主要區別在于用于生成門控信號的激活函數不同。它們的通用公式如下,其中 $ g $ 是某種激活函數。
常見的變體包括:
| 變體名稱 | 特點 |
|---|---|
| 原始 GLU | 基礎形式 |
| ReGLU | 使用 ReLU 作為門控,計算簡單,且在大型模型中表現優異(如 PaLM 論文中使用)。 |
| GEGLU | 目前最流行和效果最好的變體之一。GELU 是高斯誤差線性單元,它是 ReLU 的平滑版本,被證明在 Transformer 模型中效果非常好。 |
| SwiGLU | Swish 是另一個平滑且表現優異的激活函數,SwiGLU 在多項基準測試中表現突出。 |
GLU 的優勢與特點有:
- 緩解梯度消失:門控機制為梯度流動提供了一條“高速公路”(類似于殘差連接),使得梯度可以更有效地反向傳播,從而允許構建更深的網絡。
- 自適應學習:模型可以自適應地學習為每個特征維度分配不同的權重(重要性),而不是像傳統激活函數(如 ReLU)那樣進行固定的非線性變換。
- 提升模型表現:在實踐中,尤其是在自然語言處理領域的 Transformer 模型中(如作為前饋神經網絡 FFN 的激活函數),GEGLU 和 SwiGLU 等變體通常比傳統的 ReLU 或 GELU 激活函數表現更好。
- 參數效率:雖然 GLU 需要將特征維度翻倍來產生 A 和 B(因此輸入維度會變大),但許多研究發現,為了達到相同的性能,使用 GLU 的模型往往可以比使用標準激活函數的模型更小。
本文方法
TabNet 的設計靈感來源于決策樹,通過特定的結構設計,傳統的深度神經網絡(DNN)模塊可以模擬決策樹的輸出流形,如下圖所示。其中稀疏的實例級特征選擇是實現超平面形式決策邊界的關鍵,TabNet 的核心目標是在保留決策樹優勢(如特征選擇能力)的同時,通過深度學習提升模型性能。
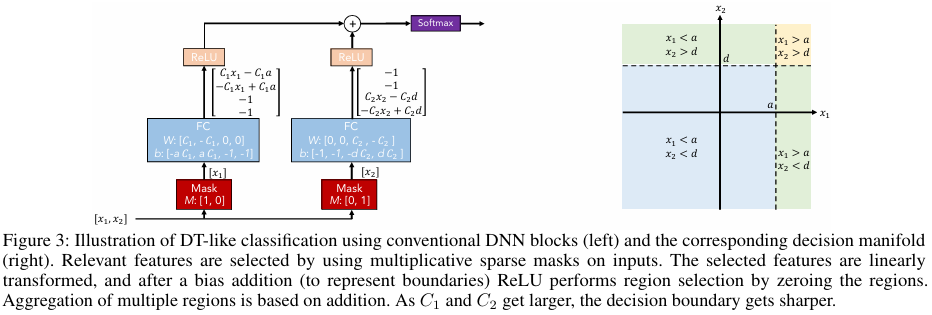
TabNet 編碼器架構
TabNet 編碼器采用多步驟序列處理結構,如下圖所示。每個決策步驟逐步處理輸入特征并聚合信息,其核心組件包括特征選擇機制和特征處理模塊。
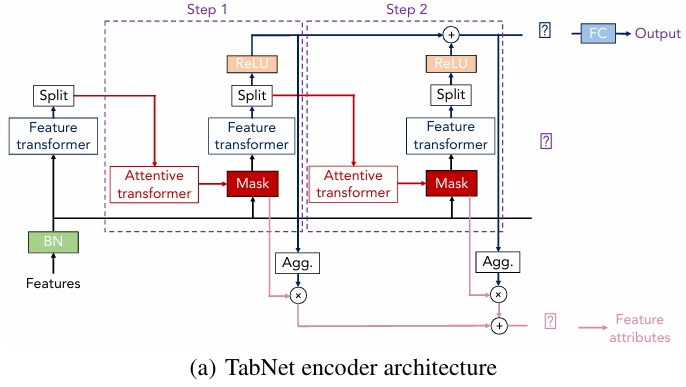
注意力變換器
特征選擇機制通過注意力變換器(Attentive Transformer) 接收前一步處理的信息 \(a[i-1]\) 生成一個稀疏掩碼 \(M[i] \in \Re^{B\times D}\),實現對特征的軟選擇(\(M[i] \cdot f\))。其結構如下圖所示,注意力變換器包括全連接層、批歸一化層和 Sparsemax 歸一化函數。

各個組件的作用如下表所示:
| 注意力變換器組件 | 作用 | 功能 |
|---|---|---|
| 全連接層 | 學習并轉換特征表示 | 將輸入的特征信息進行非線性變換,并將其映射到與原始輸入特征維度相同的空間。可以將其理解為一個可學習的評分器,為每個特征生成一個未經過規范化的原始分數,表示該特征在當前決策步驟中的潛在重要性。 |
| 批歸一化層 | 穩定內部激活值分布,加速并穩定訓練 | 深度神經網絡的各層輸入數據的分布會隨著訓練而發生變化(內部協變量偏移),這會導致訓練變得困難。批歸一化層對全連接層輸出的初步重要性得分進行歸一化處理,使其均值為 0,方差為 1。通過穩定數值分布,允許使用更大的學習率,從而加快模型的訓練速度。同時減輕了對參數初始化的敏感性,使訓練過程更加平滑和穩定。 |
| Sparsemax 歸一化函數 | 實現稀疏特征選擇 | 將重要性得分轉化為稀疏的、專注于少數關鍵特征的掩碼。 |
該步驟的公式如下,其中 \(P[i]\) 是先前特征使用程度的先驗尺度項,定義為 \(P[i] = \prod_{j=1}^{i}(\gamma - M[j])\),\(\gamma\) 為松弛參數。
Sparsemax 歸一化確保了掩碼的稀疏性。接著引入稀疏正則化損失 \(L_{sparse}\) 以控制特征選擇的稀疏性,其公式如下所示:
特征變換器
特征處理模塊使用特征變換器(Feature Transformer) 處理被選中的特征,其結構包含共享層(跨步驟參數復用)和決策步驟依賴層,每層由全連接層、批歸一化(BN)和門控線性單元(GLU)非線性激活組成,如下圖所示。
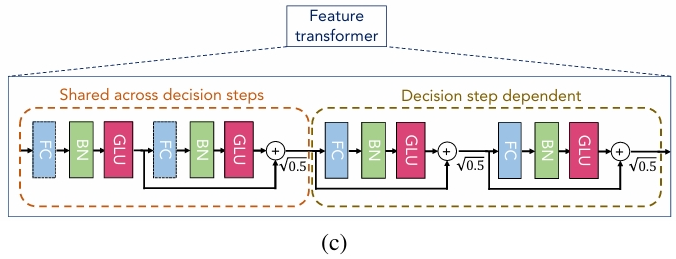
數據流為:輸入 → 全連接層(線性變換) → 批歸一化層(穩定分布) → GLU(非線性門控) → 與輸入進行歸一化殘差相加(信息融合與穩定),各個組件的作用如下表所示:
| 特征變換器組件 | 作用 | 功能 |
|---|---|---|
| 全連接層 | 實現特征的線性組合與交互 | 通過一個權重矩陣將輸入向量映射到新的特征空間,使得模型能夠學習到輸入特征之間復雜的線性關系。 |
| 批歸一化層 | 穩定訓練并加速收斂 | 對全連接層的輸出進行標準化處理(使其均值為 0,方差為 1) |
| 門控線性單元 | 引入可控的非線性 | 提供一種高效且可控的非線性激活機制,模擬信息門控 |
| 歸一化殘差連接 | 避免網絡退化,確保梯度有效傳播 | 模塊內部采用了殘差連接,并將殘差路徑的輸出乘以一個縮放因子。通過殘差連接,確保了即使深層網絡發生退化,底層的信息也能直接傳遞到后方,保證了模型的基準性能。縮放操作有助于確保網絡中各層的方差不會發生劇烈變化,從而進一步穩定訓練過程。 |
如果每個步驟都使用完全獨立、不共享參數的特征變換器,會導致模型參數量急劇增加,容易過擬合,并且訓練效率低下。反之,如果所有步驟都強制共享同一個變換器,模型又可能缺乏足夠的靈活性來為每個步驟學習獨特的特征表示。因此,特征變換器由兩個共享層和兩個決策步驟依賴層組成,其核心動機是:在參數效率 和表示靈活性之間取得最佳平衡。兩部分的具體作用如下:
| 層次 | 作用 | 功能 |
|---|---|---|
| 共享層 | 學習通用的、與決策步驟無關的特征基礎表示 | 這些層的參數在所有決策步驟之間是共享的。由于每個步驟處理的是相同的原始特征集,共享層可以學習如何對這些特征進行一種“通用”的、基礎的非線性編碼。這種參數復用提高了模型的參數效率,避免了不必要的重復學習,使模型更加緊湊,并有助于減少過擬合的風險。 |
| 決策步驟依賴層 | 學習特定于當前決策步驟的、專門化的特征表示 | 這些層的參數是每個決策步驟獨有的。由于 TabNet 的每個步驟通過注意力機制選擇了不同的特征子集,每個步驟的“任務焦點”是不同的。在共享層完成了基礎特征提取之后,步驟依賴層可以根據當前步驟的特定任務,對特征進行進一步的、專門化的加工,實現針對當前步驟所關注的特征子集,學習最有效的深層表示。 |
所有決策步驟(Step 1, Step 2, ..., Step N)中的這 2 個共享層共享同一套參數,每個決策步驟的步驟依賴層 1 和步驟依賴層 2 都擁有自己獨有的一套參數。這兩部分以串聯方式協同作用,數據流如下:輸入特征 → 共享層1 → 共享層2 → 步驟依賴層1 → 步驟依賴層2 → 輸出 \([d[i], a[i]]\)。模塊輸出的兩部分含義為:當前步驟的決策貢獻 \(d[i]\) 和傳遞給下一步的信息 \(a[i]\),即 \([d[i], a[i]] = f_i(M[i] \cdot f)\)。
TabNet 編碼器數據流
TabNet 編碼器的預測輸出流程是一個從多步驟決策貢獻聚合到線性映射的過程,核心在于將每個決策步驟的學習成果合并,最終通過一個簡單的輸出層得到預測值。TabNet 編碼器的數據流如下:
- 使用注意力變換器生成掩碼:輸入來自前一個決策步驟的處理后信息 \(a[i-1]\),對于第一個步驟有特定的初始化方式。該信息通過一個可學習函數 \(h_i\),由全連接層和批歸一化層實現。輸出結果與先驗尺度項 \(P[i-1]\) 相乘,\(P[i-1]\) 記錄了每個特征在之前步驟中被使用的累積情況。這一機制鼓勵模型在后續步驟中關注之前使用較少的特征,促進探索。經過調制后的結果通過 Sparsemax 歸一化函數,生成一個稀疏的、實例特定的特征選擇掩碼 \(M[i]\) 輸出。
- 應用掩碼進行特征過濾:將上一步生成的掩碼 \(M[i]\) 與原始的輸入特征 \(f\) 進行逐元素相乘(Hadamard 積),得到過濾后的特征 \(M[i] · f\)。在此過程中,被掩碼忽略的特征(對應
M[i]值為0)將不參與當前步驟的后續計算,從而確保模型容量集中于最顯著的特征上。 - 使用特征變換器進行非線性變換:輸入過濾后的特征 \(M[i] · f\) 給特征變換器 \(f_i\),通過共享層(所有決策步驟參數共享)學習通用的特征變換,再通過步驟依賴層(每個步驟參數獨有)學習針對當前步驟的特定表示。特征變換器輸出一個被深度編碼的特征表示,并分割成兩個部分:當前步驟對最終決策的貢獻 \(d[i] ∈ ?^(B×N_d)\)、傳遞給下一步驟注意力變換器的信息 \(a[i] ∈ ?^(B×N_a)\)。
- 信息聚合與傳遞:當前步驟的決策貢獻 \(d[i]\) 將被暫存,所有步驟的 \(d[i]\) 最終會通過聚合形成總體決策嵌入。信息 \(a[i]\) 被直接送入下一個決策步驟(第 \(i+1\) 步)的注意力變換器作為其輸入,開始新一輪的特征選擇與推理循環。
- 是更新先驗尺度:在完成當前步驟后根據新生成的掩碼 \(M[i]\) 更新先驗尺度 \(P[i]\),為下一個步驟的特征選擇做好準備。
最后 TabNet 通過“多步驟特征選擇與推理 → ReLU 激活的決策貢獻聚合 → 線性層映射 → Softmax/Argmax 輸出”得到預測結果。TabNet 采用了一種線性求和的方式,并引入非線性激活函數來保證穩定性,將所有 \(N_{steps}\) 個步驟的決策貢獻合并為一個總體表示:
得到一個融合了所有步驟信息的總體決策嵌入向量\(d_{out} \in \Re^{B \times N_d}\) 后,TabNet 使用一個線性映射層(即一個全連接層)來生成最終的預測結果:\(\text{Output} = W_{final} \cdot d_{out}\)。
可解釋性設計
TabNet 通過以下機制提供局部和全局可解釋性:
- 局部解釋:每一步的掩碼 \(M[i]\) 顯示該步驟所選特征。
- 全局特征重要性:通過聚合各步驟的掩碼權重,計算整體特征重要性 \(M_{agg}\):\[M_{agg-b,j} = \sum_{i=1}^{N_{steps}} \eta_b[i] M_{b,j}[i] / \sum_{j=1}^{D} \sum_{i=1}^{N_{steps}} \eta_b[i] M_{b,j}[i] \]其中 \(\eta_b[i] = \sum_{c=1}^{N_d} \text{ReLU}(d_{b,c}[i])\) 表示第 \(i\) 步對決策的貢獻度。
TabNet 解碼器與自監督學習
TabNet 的解碼器主要用于實現自監督學習任務,其核心目標是從編碼器生成的表示中重建出原始的表格特征。解碼器將編碼過程中分散在各個決策步驟的信息重新整合和上采樣,以恢復原始輸入。其輸入是編碼器的輸出表示,即經過多個決策步驟處理并聚合后的信息。它的最終輸出是重建的特征向量,其維度與原始輸入特征相同。解碼器由一系列特征變換器 和全連接層構成,結構如下圖所示:

其工作流程可以概括為以下幾個步驟:
- 逐步驟的特征變換:使用特征變換器塊實現。解碼器為每個決策步驟(從第 1 步到第 N_step 步)都配備了一個獨立的特征變換器,這些變換器在結構上與編碼器中使用的特征變換器類似。編碼器每個步驟輸出的中間表示會被分別送入解碼器對應步驟的特征變換器中進行處理,實現對編碼后的信息進行初步的逆變換和增強,為重建特征做準備。
- 使用全連接層進行特征維度映射:在每個決策步驟中,經過特征變換器處理后的數據會通過一個全連接層,主要功能是將高維的、抽象的編碼表示映射回原始特征的維度(D 維),將深度特征空間轉換回原始的表格特征空間。
- 步驟輸出的聚合:解碼器將所有決策步驟經過全連接層重建出的特征向量進行逐元素相加,得到一個最終的重建特征向量。這種求和操作基于一個假設:編碼器的每個決策步驟都學習并編碼了輸入數據的不同方面。因此在重建時,需要將所有步驟所貢獻的信息重新聚合起來,才能更完整地恢復原始輸入。
TabNet 解碼器的結構雖然比編碼器簡單,但其實現了從高層表示到原始特征空間的重建映射。它采用多步驟并行變換再聚合的方式,鏡像了編碼器的學習過程。
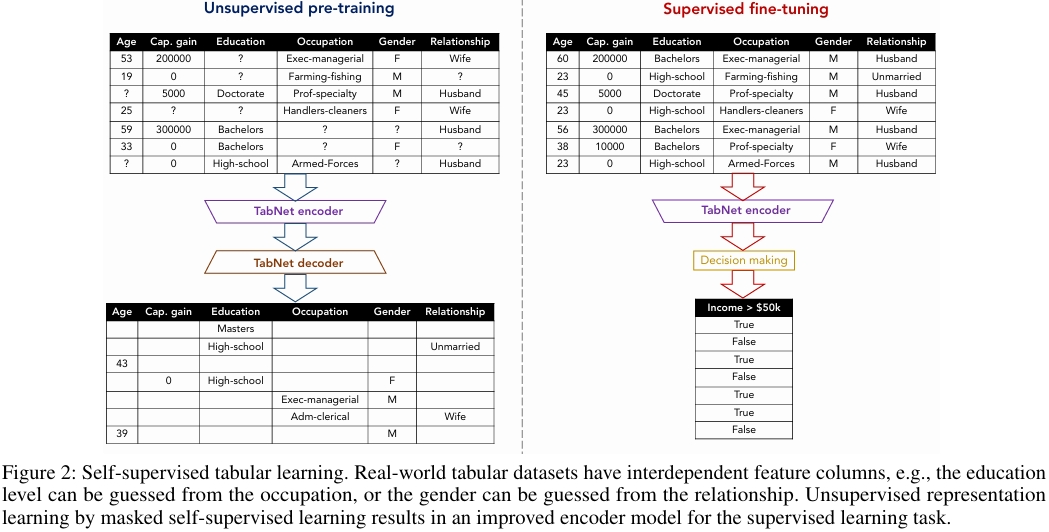
其具體流程如下:
- 輸入掩碼:一個二進制掩碼 \(S \in \{0,1\}^{B\times D}\) 被應用于原始特征 \(f\),生成一個部分被掩蓋的輸入 \((1-S) \cdot \hat{f}\)。其中,值為 0 的位置表示該特征值被掩蓋(未知),需要模型預測。
- 編碼過程:編碼器接收被掩蓋的輸入 \((1-S) \cdot \hat{f}\)。為了引導編碼器只關注已知特征,先驗尺度P[0]被初始化為 \((1-S)\)。這意味著被掩蓋的特征在第一步就被標記為“已使用”,從而被模型忽略。
- 解碼與重建:編碼器產生的表示被送入解碼器。解碼器輸出重建的所有特征。
- 損失計算:損失函數僅計算在被掩蓋的特征(即S矩陣中值為1的位置)上的重建誤差。文檔中采用的損失是經過標準差歸一化后的均方誤差,這樣做的好處是讓不同尺度的特征對損失的貢獻相對均衡。
實驗結果
實例級特征選擇的有效性
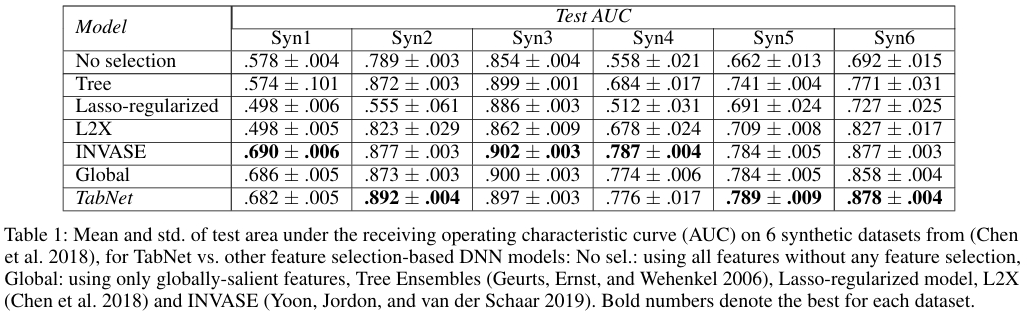
實驗首先在 6 個合成數據集(Syn1-Syn6)上進行,這些數據集被設計為只有特征的一個子集決定輸出結果,其中 Syn1-Syn3 是全局重要特征,Syn4-Syn6 是實例依賴的重要特征。實驗結果如下表所示,TabNet 的性能優于或與其他特征選擇方法(如 L2X, INVASE)相當。在全局重要特征數據集(Syn1-Syn3)上,TabNet 的性能接近 Global 方法。在實例依賴特征數據集(Syn4-Syn6)上,TabNet 通過消除實例級冗余特征,性能超過了“Global”方法。TabNet 的參數量(26k-31k)遠少于 INVASE 等需要多個模型的方案(101k),體現了其參數效率。
真實數據集上的性能
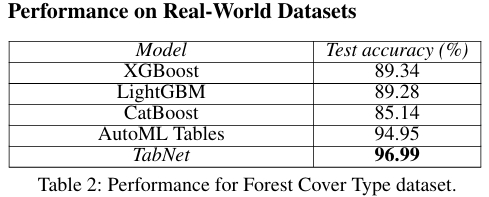
實驗在多個真實世界數據集上進行了測試,包括分類和回歸任務。Forest Cover Type(森林覆蓋類型分類)任務需要根據制圖變量分類森林覆蓋類型,結果可見 TabNet(96.99% 準確率)顯著優于 XGBoost、LightGBM 等梯度提升樹模型,甚至超過了經過自動化超參數搜索的 AutoML Tables 框架(94.95%)。
Poker Hand(撲克手牌分類)任務需要根據撲克牌的花色和等級分類手牌,這是一個具有確定性規則但數據高度不平衡的任務。實驗結果可見傳統 MLP、DT 及其混合模型表現不佳,梯度提升樹略有提升但準確率仍低(約 71%)。TabNet 取得了接近規則方法的優異性能(99.2%),體現了其處理復雜非線性關系的能力。

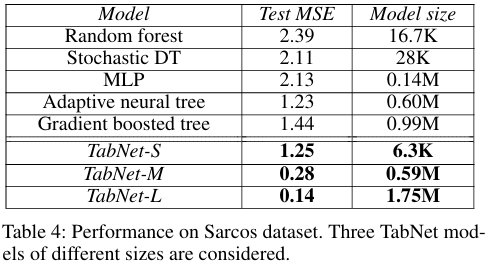
機器人逆動力學回歸的任務是回歸擬人機器人手臂的逆動力學,實驗結果為在模型大小受限時(TabNet-S,6.3K 參數),TabNet 與參數量大 100 倍的最佳模型性能相當。當不限制模型大小時(TabNet-L,1.75M 參數),TabNet 的測試 MSE(0.14)比現有最佳模型低一個數量級。
Higgs Boson(希格斯玻色子分類)的目的是區分希格斯玻色子信號與背景噪聲,實驗結果為在大規模數據集(1050 萬實例)上 TabNet 的性能優于 MLP。且 TabNet 與先進的稀疏進化 MLP 性能相當,但 TabNet 的結構化稀疏更利于計算效率。
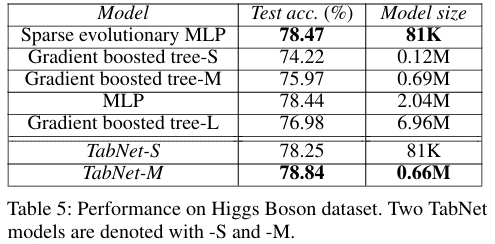
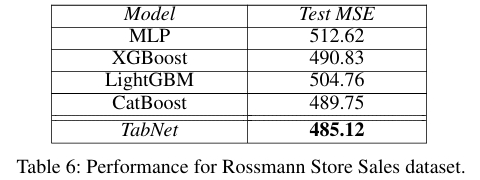
Rossmann Store Sales(零售銷售額預測)需要根據靜態和時序特征預測商店銷售額,實驗結果為 TabNet(MSE: 485.12)超越了所有對比的梯度提升樹方法。
可解釋性分析
實驗通過可視化特征重要性掩碼來展示 TabNet 的可解釋性。合成數據的可視化效果下圖所示,在 Syn2 上 TabNet 準確地將注意力集中在真正相關的特征(X3-X6)上,無關特征的重要性幾乎為零。在 Syn4 上 TabNet 能根據指示特征(X11)動態選擇不同的特征組(X1-X2 或 X3-X6)。

對于真實數據,在成人人口普查收入預測中,TabNet 給出的特征重要性排名(如“Age”最重要)與領域共識一致,并通過 t-SNE 可視化展示了“Age”特征對決策空間的清晰劃分。

自監督學習
TabNet 采用掩碼特征預測任務進行無監督預訓練,然后用有標簽數據對模型進行微調。在 Higgs 數據集上,隨著有標簽數據量的減少,預訓練帶來的提升越明顯。當有標簽數據為 1k 時,預訓練將準確率從 57.47% 提升至 61.37%。即使有標簽數據增至 100k,仍能觀察到性能提升。

如下圖所示,自監督預訓練不僅提升了最終性能,還大幅加快了模型收斂速度,這對于持續學習和領域自適應非常有益。

優點和創新點
個人認為,本文有如下一些優點和創新點可供參考學習:
- TabNet 創新性地采用了序列注意力機制,實現了實例級的軟特征選擇,使模型在每一步決策中都能動態、稀疏地聚焦于當前最相關的特征子集;
- 該模型成功統一了高性能與內在可解釋性,通過可視化每一步的特征選擇掩碼,既能提供局部實例的解釋,也能聚合得到全局特征重要性;
- 本文將掩碼自監督學習框架引入表格數據,通過預測被掩碼的特征進行預訓練,能夠有效利用無標簽數據來提升下游監督任務的性能。


 浙公網安備 33010602011771號
浙公網安備 33010602011771號