雖然說是手算，但是我還是會寫一點 C# 代碼，避免敲壞了計算器。我和大家保證，整個手算過程中，最終的計算結果只需要用到初高中知識。推導過程會用到部分高數的知識。我盡量將用到的知識點全列舉出來，本文對學渣友好，期望能夠拿出紙筆和 VisualStudio 的伙伴閱讀完本文能夠真的理解神經網絡BP傳播算法是如何計算的

雖然說是手算，但是我還是會寫一點 C# 代碼，避免敲壞了計算器。我和大家保證，整個手算過程中，最終的計算結果只需要用到初高中知識。推導過程會用到部分高數的知識。我盡量將用到的知識點全列舉出來，本文對學渣友好，期望能夠拿出紙筆和 VisualStudio 的伙伴閱讀完本文能夠真的理解神經網絡BP傳播算法是如何計算的

看了一下時間，今年確實 2025 年，而不是 2015 年。在 2025 時還在聊BP 算法實在有點一言難盡。我在 10 多年前嘗試寫過貼近的程序，當時寫的時候有一些概念沒有理解，但代碼是寫了也能跑，甚至于在當時世界上最快的超級計算機跑了我的代碼。但不能理解的部分就是不能理解。最近在散步的時候，我的伙伴 https://github.com/SeWZC 和我說明白了求偏導的數學意義。我當初高數學了3年，別人都是只學一年（因為我不斷掛科），那會以為偏導沒有什么，于是缺了一個知識點，導致我對 BP 的部分理解錯誤。盡管代碼能跑，也能符合預期進行訓練，但里面關于傳播算法中，如何計算各個權重參數的過程我是不能全說明白的。我最近理解了偏導的數學意義之后，再到知乎上閱讀了 通俗理解神經網絡BP傳播算法(https://zhuanlan.zhihu.com/p/24801814 ) 文章，嘗試按照知乎文章的給定的內容和方法，自己手算了一遍，我就完全理解了之前我所寫的代碼了。擔心本金魚會忘了之前的想法，或者擔心下次和伙伴聊天的時候又說錯了，我就編寫了本文。可以認為本文沒有給出比 通俗理解神經網絡BP傳播算法(https://zhuanlan.zhihu.com/p/24801814 ) 文章更多的內容，只是按照我自己的方式一步步推導和計算。閱讀完本文，預期大家能夠對神經網絡有了更明了的理解。如果大家還是在迷迷糊糊地訓練人工智能做玄學的活，那閱讀本文可以讓大家能夠稍微有點落地的感覺，至少大概知道簡單的 BP 神經網絡是如何工作起來的

我努力讓大家盡量少知識地開局

開始之前，期望大家已經聽說過一些神經網絡的概念。這里只要求聽說過，不解其中的內容也沒關系，有部分概念我沒提到的，也許大家看完了自然就能明白，或閱讀完本文之后再繼續在網上搜關鍵詞繼續了解。期望聽說過的概念有：神經網絡、圖論、矩陣、激活函數、損失函數、權重

神經網絡可以理解圖論上的一張圖，盡管在幾乎所有的科普文章中，都會使用到矩陣，但從原理上說都是圖論的一張圖。經費有限，有了節省矩陣的出場費，本文就不帶入矩陣的內容了，直接平鋪進行計算。本文也不會用到多少圖論的知識，只是用了一點圖論上的概念。本文介紹的手算的神經網絡是一個簡單的有向圖，只有5個點。即使沒有了解過圖論的伙伴，也許通過示意圖也能夠看懂

本文的手算內容是假定咱就是一個無情的計算機，正在被訓練的人工智能。咱的需要計算出圖上（圖論的圖）的各個點的權重。為了讓人類更方便理解，以下圖中，我給定了明確的數值。假定輸入是兩個數字，期望經過咱訓練出來的神經網絡之后，能夠獲取符合預期的輸出數字。這樣的模擬情況，就能夠覆蓋非常多的情況了。也許有伙伴此時還會有一些疑惑，沒關系，先帶著疑惑看下去吧，我也不能一口氣全交代清楚情況

以下是咱的神經網絡圖（圖論的圖）的示意圖

其中 a 和 b 兩個點負責輸入，e點負責輸出。各個點之間的連接存在權重，其示意圖如下，下圖的 wxx 表示的就是各個邊的權重。寫成 wxx 的形式其實就是在隱含矩陣的概念了，只是咱本文這里不需要請出矩陣而已，如果真套上矩陣的話，這里的權重就是 w行列的表示法，即 w21 就是表示第2行第1列的值。這也是一個習慣表示方法

假定有輸入源 x0=0.35 x1=0.9 , 期望的輸出是 \(y_{out}=0.5\)。這就是一組訓練值，當然了，在實際的神經網絡訓練里面，肯定會給許多組訓練值的。只是現在換成人類手算，需要降低難度，就只要求訓練這一組數據。假定沒有神經網絡，就是一個正常人類在拿到 x0=0.35 x1=0.9的輸入，要求寫出一個函數，讓這個函數能夠根據此輸入計算出 \(y_{out}=0.5\) 的值，估計也沒那么簡單（禁止直接寫 \(f(x0,x1)=0.5\) 這樣的拖出去打靶的函數）

為了更加方便大家理解，這里先給各個權重添加隨機的初始值。初始值很多時候真的是隨機給的，依靠的是訓練過程中不斷算法修改參數，從而訓練出一個可用的神經網絡。咱現在這個神經網絡只是期望訓練出當拿到 x0=0.35 x1=0.9 的輸入時，能夠返回 \(y_{out}=0.5\) 的輸出。標記了添加了隨機權重初始值的示意圖如下

好的，勤奮的伙伴可以開始拿出紙筆，在紙上畫出以上示意圖內容了。云程序猿們沒有紙筆那就進入幻想模式，我不會讓大家不至于說沒紙筆就看不下去的
對于一個正常的神經網絡來說，每個點就是一個神經元，神經元里面包含了激活函數。在本文這里選定的 \(f(x)\) 激活函數的定義如下

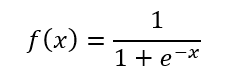
世界上的激活函數有許許多多，沒有說一定要用哪個激活函數，大家也可以在閱讀完本文之后，自己嘗試其他的激活函數

在本文的 BP 神經網絡里面，是取所有的輸入乘以各自的權重之和，進入激活函數計算，從而得到輸出。我將取所有的輸入乘以各自的權重之和記為 \(z_n\)，將經過激活函數之后的輸出記為\(y_n\) ，其示意圖如下

也許大家看到這里開始有疑惑了，憑什么神經網絡是這樣子的。沒為什么，最簡單的神經網絡只需要一個神經元即可，但一個神經元能做的事情就太弱了。雖然本文的圖（圖論的圖）有5個點，但實際上 a 和 b 點都是在接收輸入，實際參與計算只有三個點，相對來說已經足夠簡化了。在閱讀完本文之后，大家也可以試試玩玩更多點和更多層的神經網絡，只不過這時候就需要多寫寫代碼啦，全靠手算可有點難哦
似乎現在這個示意圖看起來就有些復雜了，但相信如果是一步步看下來的伙伴，自然能夠很快理解示意圖的內容了

寫到這里，咱距離整個簡單 BP 神經網絡就只剩下 損失函數（Loss Function）的定義了。簡單說明損失函數就是用來度量神經網絡輸出的值與預期期望值的差異程度的函數

損失函數要能反饋結果和預期的距離，且還要能夠求導有意義。一聽到反饋結果和預期的距離，大家可能想到的就是直接減就可以了，如這樣的一個函數\(C=y_2-y_{out}\)，但在后續步驟里一求導就約分沒了，算出來的\(C^{'}=1\)，自然就無法繼續進行下去了。那求差的平方呢，如\(C=(y_2-y_{out})^2\)呢？這個就好多了，加上平方也不用去煩惱絕對值的問題了，那自然就求結果和預期的差的平方好了。試試看求導的結果 \(C^{'}=2y_2-2y_{out}\)，這一求導發現約分出了2的值，那索性繼續乘以二分之一好了，這樣求導返回結果剛好就是簡單的減法，計算機看了非常開森。于是決定出來的損失函數定義如下

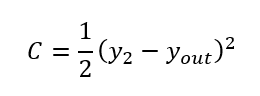
看到這里相信大家也感受到了照現在的人類的數學能力還不能讓大家隨意寫一個函數，就能獲取預期的結果。在本文的手算過程中，也許大家也就能夠理解神經網絡的能力邊界。所使用的各個函數都有一些原因，不一定是期望獲取咋樣的結果就能用對應的函數，還需要所使用的函數剛好從數學上能夠幫助后續的計算

如此咱的所有內容就都定義完成了。為了防止大家忘記現在的狀態，我再次放入當前的示意圖，咱接下來就按照這個意義圖開始將自己當成一個神經網絡，進行手算過程

拿出紙筆的伙伴可以將上述的示意圖抄在草稿紙上，咱現在就來開始第一輪的計算過程。打開了 VisualStudio 的伙伴，還請創建好控制臺項目，開始記錄一些代碼，先是一些初始化的變量或常量的值。為了確保讓大家能夠校驗自己的計算結果內容，我這里的代碼就寫固定值，而不是使用隨機數，這樣也好方便紙筆手算的伙伴對比計算差異

const double x0 = 0.35;
const double x1 = 0.9;

const double y_out = 0.5;

var a = x0;
var b = x1;

var w11 = 0.1;
var w12 = 0.8;

var w21 = 0.4;
var w22 = 0.6;

var w31 = 0.3;
var w32 = 0.9;

var count = 0;

看到以上的代碼，也許有伙伴有疑惑，以上代碼中的 y_out 是不是不符合 C# 代碼規范？我這里是借用 Latex 的表示，表示 y_out 常量，按照 Latex 寫法就是 y_out 啦。因此就不要將其改成 yOut 或 YOut 哦

來進行一步步的計算過程，求 \(z_0\) 的值

對應的代碼實現如下

var z0 = w11 * a + w12 * b;

這個過程看起來十分簡單，就是將所有進入 c 點的輸入乘以對應的權重返回的和。同理繼續計算d點的\(z_1\)的值

對應的代碼如下

var z1 = w21 * a + w22 * b;

分別讓 \(z_0\) 和 \(z_1\) 經過 \(f(x)\) 激活函數，可分別得到 \(y_0\) 和 \(y_1\) 的值

也許大家用計算器算出來的小數點精度有些差異，但只要前面幾位差不多就可以，對于神經網絡來說不用太精確
對應的代碼如下，封裝了 F 函數

double F(double x)
{
    return 1.0 / (1 + Math.Pow(Math.E, -x));
}
var y0 = F(z0);
var y1 = F(z1);

繼續計算 \(z_2\) 的值

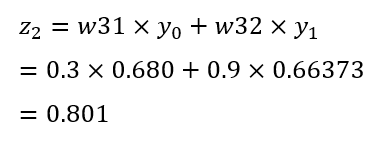
對應的代碼如下

var z2 = w31 * y0 + w32 * y1;

讓 \(z_2\) 經過激活函數，可得到\(y_2\)的值

對應的代碼如下

var y2 = F(z2);

此時可見這一輪的輸出\(y_2\)距離預期的\(y_{out}\)還有點距離。具體度量的距離有多大，那就要經過損失函數計算看

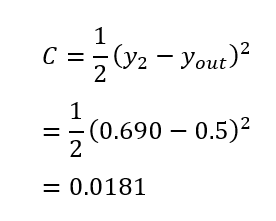
對應的代碼如下

var c = C(y2);
static double C(double y2)
{
    return 1.0 / 2 * Math.Pow((y2 - y_out), 2);
}

完成了第一輪計算，接下來就是進行第一輪訓練，進行 BP 的傳播算法。此時在推導計算過程，就需要用到偏導的知識了。其中包括了偏導的鏈式計算和對函數求導的知識。借用從 http://www.rzrgm.cn/awei040519/articles/18529084 博客的一張圖來說明偏導在這里的意義。在這里的意義就是假定輸入到輸出中間經過的神經網絡的某些權重變量計算之后，能夠獲取預期的輸出內容，求解神經網絡中的權重變量的值。這個求解過程有解，即是求讓損失函數快速到達一個極小點。在偏導意義里面，極大和極小這些極值是相同的，從極大到極小的轉換只需乘以負一即可

沒有經過損失函數可不可以？可以的，但是存在的問題是，如果不用隨機數隨便亂碰，那怎么能夠知道各個權重應該如何調，應該是朝著加號方向調還是減號方向調好呢。假定咱有無窮的計算時間，那就不停各個參數加0.00001或0或-0.00001給他全遍歷即可，這樣自然能夠獲取很（不敢說最哈）優解。但大家肯定也看出來問題，這樣的做法需要大量的時間，且隨著圖（圖論的圖）上的點越多，這個計算時間就會越長，且是排列組合的快速加長，也許此時只有量子計算機才能計算了。聰明的數學家想到了利用數學上的偏導工具，協助更快速求較優解的權重數值解。如上圖所示，利用偏導數協助求某一個切面上的函數導數的極值方向從而讓權重的修改能夠更快到達較優解，如從 https://zhuanlan.zhihu.com/p/1945144971243000845 拷貝的動圖所示

讀過高數的伙伴也許有疑惑，由于偏導只是求一個切面方向上的，而整個網絡是依靠多個權重一起工作的，那是否會導致畫出來的函數圖實際上有多個極值呢？沒錯，這就是局部最優解陷阱。好在本文這里足夠簡單，還不會踩到這個坑。進入局部最優解陷阱時，也許經過了很多輪的訓練，其輸出也不能達到預期，這時候就是大佬們常說的煉丹結果是廢丹了，需要重新修改權重為隨機數重新煉丹

求出來各個權重對應偏導數值之后，就可以更新各個權重的值，進行下一輪計算。下一輪計算結果輸出之后，再經過損失函數判斷是否結果已經接近了。如果不接近，則再次求各個權重對應偏導數值，用各個權重對應偏導數值更新各個權重的值，再進行下一輪計算。這樣的過程就是簡化后的 BP 神經網絡訓練的過程。其計算方式如下，以下列舉的公式中帶“’”的部分表示更新之后的權重的值

通過以上公式不難看出，其中的核心點就是在于如何求偏導。只要求出偏導了，那自然就有了更新權重的數值的方法了

開始求偏導準備來修改權重參數。開始之前先簡單介紹鏈式法則的計算方式。在本文用到的偏導知識部分非常少，本文也只介紹本文需要用到的部分知識。假定有一個參數 x 計算出了 y 的過程中，經過了兩個步驟，先經過了 g 函數，求出了 t 結果。再將 t 結果傳入 f 函數，從而計算出 y 結果。此時求x的偏導則可用以下的公式

可以看到，此時將計算拆分為兩步，先求t的偏導，再求x的偏導。如此過程恰好就可以用在神經網絡上，逐層逐個求偏導，且剛好可以實現累加的過程。當然，本文為了簡單起見，不會減少計算過程，沒有將計算過的值緩存起來省略重新計算的過程，但相信大家看到后面一眼就看出來重復部分很簡單就可以省略重復計算

如求w31的偏導，就可以從y2到z2再到w31這樣一步步求偏導做乘法，如以下示意圖所示

如此即可得出以下公式

這個過程里面，各個步驟都是一個簡單的確定的函數，求偏導過程也就很簡單了。不需要說整個一路將 w31帶入到最終計算式里面。大家如果好奇真的一路將w31帶入表達式里面，最終損失函數C有多長，且求導稍微困難。通過鏈式的方式可以進行一級級的計算，整體復雜度也能夠降低

接下來咱來開始一步步求這個偏導的內容

相信大家的求導知識還沒忘記，求導數學意義上就是求速率。如對于常量函數，如 y=5 的函數，其速率就是平的，如下圖所示，自然求出來的導數就是 0 的值

求偏導的話，只要對求偏導的變量當成變量，其他當成常量計算。這也就是為什么求出來的式子里面 \(1/2 y_{out}^2\) 會是0的值的原因。那對于一次函數呢，如y=2x 函數呢，其導數反映的速率就剛好是變量前面的系數了。如下圖所示

于是就有

那平方呢？平方的話，可以認為速率需要乘以變量自身，幾倍方就是幾倍速率

于是就有

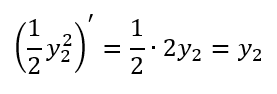
回顧一下，整條式子算起來就是

是不是看到這里感覺損失函數確實不是隨便選的，剛好這個函數能夠非常好的適應求導的結果。求導結果里面非常方便進行計算，計算機看了非常開森，因為求導結果是兩個已經計算出結果的值，而且只做減法。在第一輪訓練結果里面，相信大家能夠直接口算結果

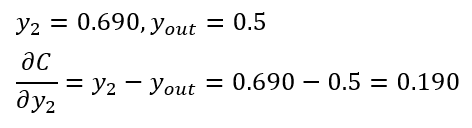
看吧，沒騙大家，只有過程推導用到了一點高數的知識，最終計算都是小學到高中的知識，且大部分都是小學知識

希望看到這里的大家會有很多信心，接下來開始解下一個偏導內容，這是最難的一個部分了

激活函數求導過程如下，咱選用的激活函數都是現成的，有很多大佬幫忙求導過了的函數的。如果大家感覺這個過程有點難，那也可以跳過，直接看求導結果就可以了

可以看到激活函數求導結果也是非常開森的計算，直接就是 fx·(1-fx) 的值，計算非常簡單。試試代入公式

看起來這也是非常簡單的小學數學就能完成計算結果，雖然本次計算過程有點難，但結果卻是簡單的。也依然是計算機非常開森的計算表達式，都是已知的變量的基礎加減乘除計算

最后一步的求導就特別簡單啦

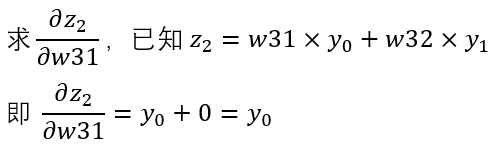
因為只對w31求偏導，于是 w32 就可以視為常量。本身y0和y1就是被視為常量，直接 w32 乘以 y1就算出0的值。而y0作為w31的系數，求導結果就是y0了。這個過程看起來很解壓。好了，各個式子就在這里求完了，將其組合起來

換成代碼的話，其實現如下

var dc_dw31 = (y2 - y_out) * (y2 * (1 - y2)) * y0;

不知道大家這一步求出來的結果是否和我的接近呢

第一步的求偏導計算咱算了很久，后續的步驟咱就能快非常多了。如對w32求偏導，可以看到只有最后一條式子有所不同

代碼實現如下

var dc_dw32 = (y2 - y_out) * (y2 * (1 - y2)) * y1;

從這里也可以看到對 w31 和 w32 求偏導，也只有最后一個乘數不相同而已。對于程序猿來說，看到有很多相同的代碼，本能地自然就會去想優化，這是非常正確的，那就作為課后作業給到大家去優化啦

下一步嘗試求w11的偏導，這一次鏈式過程就稍微長了一些了，如以下示意圖

有示意圖，相信大家很容易就知道了上面這條表達式是如何寫出來的。核心關鍵點就是倒推，看看w11在哪一級表達式中，然后再繼續往上找，直到能到達C損失函數里去。這個過程就類似于已知樹（圖論的樹）進行求到根的路徑的過程。求導數的前面兩項咱已經在w32求偏導中計算過了，其結果如下

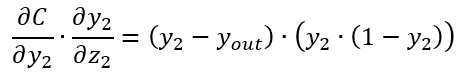
接下來的各項的求導過程如下

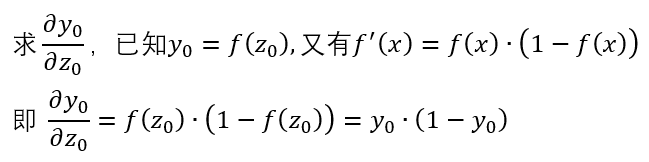
將幾個表達式合起來，即可計算結果

表達式雖然長，但拆開看卻非常清晰，如下圖所示

以上的各個變量參數都是已經計算出結果的，其整個表達式最終結果也是非常簡單的小學計算題。計算結果是 0.000929 的值

寫成代碼如下

var dc_dw11 = (y2 - y_out) * (y2 * (1 - y2)) * w31 * (y0 * (1 - y0)) * a;

同理來求 w12 的偏導，接近和 w11 相同，其差別只有最后的一步計算。如下示意圖所示

可見計算公式為

對應的代碼實現如下

var dc_dw12 = (y2 - y_out) * (y2 * (1 - y2)) * w31 * (y0 * (1 - y0)) * b;

同理也可以繼續求w21的偏導

通過以上示意圖可知

各自代入可得

對應的代碼如下

var dc_dw21 = (y2 - y_out) * (y2 * (1 - y2)) * w32 * (y1 * (1 - y1)) * a;

按照以上求偏導方式，可得

對應的代碼如下

var dc_dw22 = (y2 - y_out) * (y2 * (1 - y2)) * w32 * (y1 * (1 - y1)) * b;

最后將各個權重減去對應的偏導，更新之后的權重我給它上面多標了一瞥

對應的代碼如下

w31 = w31 - dc_dw31;
w32 = w32 - dc_dw32;

w11 = w11 - dc_dw11;
w12 = w12 - dc_dw12;

w21 = w21 - dc_dw21;
w22 = w22 - dc_dw22;

按照更新的值再跑一遍計算，可得到y2輸出為 0.6820 的值，求損失函數為 0.0165 的值，可以看出比原來的第一遍計算得到的 0.0181 更小，證明更加貼近。好在我過程中順帶編寫了代碼，可以愉快地讓計算機幫我跑個100次，跑了100次之后的各個值如下

w11=0.099497286575324431
w12=0.79870730833654868
w21=0.35650028026826369
w22=0.48814357783267731
w31=-0.30047225429264057
w32=0.32533602822418006
y2=0.50076396515258481
c=2.9182137718196697E-07

可見看到此時輸出的 y2 已經非常貼近預期的輸出了。于是大家可以開森地認為咱手算訓練出一個能夠當輸入為 x0=0.35 x1=0.9時，獲得0.5輸出值的簡單BP神經網絡啦

相信看了整個過程的大家也能感受出來，本文選用的例子中所涉及的計算是非常簡單的。再回頭看看總的代碼，可見實現代碼量是非常少的

const double x0 = 0.35;
const double x1 = 0.9;

const double y_out = 0.5;

var a = x0;
var b = x1;

var w11 = 0.1;
var w12 = 0.8;

var w21 = 0.4;
var w22 = 0.6;

var w31 = 0.3;
var w32 = 0.9;

var count = 0;

while (true)
{
    var z0 = w11 * a + w12 * b;
    var z1 = w21 * a + w22 * b;

    var y0 = F(z0);
    var y1 = F(z1);

    var z2 = w31 * y0 + w32 * y1;

    var y2 = F(z2);

    var c = C(y2);

    if (c < 0.0000001)
    {
        break;
    }

    var dc_dw31 = (y2 - y_out) * (y2 * (1 - y2)) * y0;
    var dc_dw32 = (y2 - y_out) * (y2 * (1 - y2)) * y1;

    var dc_dw11 = (y2 - y_out) * (y2 * (1 - y2)) * w31 * (y0 * (1 - y0)) * a;
    var dc_dw12 = (y2 - y_out) * (y2 * (1 - y2)) * w31 * (y0 * (1 - y0)) * b;

    var dc_dw21 = (y2 - y_out) * (y2 * (1 - y2)) * w32 * (y1 * (1 - y1)) * a;
    var dc_dw22 = (y2 - y_out) * (y2 * (1 - y2)) * w32 * (y1 * (1 - y1)) * b;

    w31 = w31 - dc_dw31;
    w32 = w32 - dc_dw32;

    w11 = w11 - dc_dw11;
    w12 = w12 - dc_dw12;

    w21 = w21 - dc_dw21;
    w22 = w22 - dc_dw22;

    count++;
}

Console.WriteLine("Hello, World!");

double F(double x)
{
    return 1.0 / (1 + Math.Pow(Math.E, -x));
}

static double C(double y2)
{
    return 1.0 / 2 * Math.Pow((y2 - y_out), 2);
}

也許此時有人會說，明明我看到的py代碼量更少，為什么換成C#的代碼量就這么多了？別急，大家試試看回憶一下上文布置的課后作業。之所以網上看到的很多py實現的版本的代碼量少，是因為使用了本文沒有付出場費的矩陣來幫忙計算，許多重復的計算邏輯被封裝起來了。試試看給以上的代碼進行優化，將重復的計算進行合并，將重復的結構進行抽象，很好，此時相信大家一和py代碼進行對比就會發現接近相同啦

本文代碼放在 github 和 gitee 上，可以使用如下命令行拉取代碼。我整個代碼倉庫比較龐大，使用以下命令行可以進行部分拉取，拉取速度比較快

先創建一個空文件夾，接著使用命令行 cd 命令進入此空文件夾，在命令行里面輸入以下代碼，即可獲取到本文的代碼

git init
git remote add origin https://gitee.com/lindexi/lindexi_gd.git
git pull origin 3621fbea66658c99f11ed4faa28aa60bb5ac4466

以上使用的是國內的 gitee 的源，如果 gitee 不能訪問，請替換為 github 的源。請在命令行繼續輸入以下代碼，將 gitee 源換成 github 源進行拉取代碼。如果依然拉取不到代碼，可以發郵件向我要代碼

git remote remove origin
git remote add origin https://github.com/lindexi/lindexi_gd.git
git pull origin 3621fbea66658c99f11ed4faa28aa60bb5ac4466

獲取代碼之后，進入 Bp/DewhigarjejelDaykogiqem 文件夾，即可獲取到源代碼

更多技術博客，請參閱 博客導航