https://codeforces.com/topic/135071

翻譯 + 一點點理解。

記答案序列為 \(ans\)。

運用貪心與 DP 的思想，我們能輕易地 \(O(n)\) 求出任意單點 \(ans_i\) 的值。

現在觀察 \(ans\) 序列的性質：它單調不增，且 \(0\le ans_k\le n/k\)。與其他題解不同的角度是：如果發現 \(ans_i=ans_j\)，那么顯然有 \(\forall i\le t\le j,ans_t=ans_i\)。于是考察一種分治做法，令 \(solve(l,r)\) 為求出 \(i\in[l,r]\) 的 \(ans_i\) 的函數。每次若 \(ans_{l-1}=ans_{r+1}\)，那么可以直接得出 \([l,r]\) 里面全部值均為 \(ans_{l-1}\)；否則直接算出 \(ans_{mid}\) 的值，遞歸 \(solve(l,mid-1)\) 與 \(solve(mid+1,r)\) 計算。

顯然每次 \(solve(l,r)\) 時 \(ans_{l-1},ans_{r+1}\) 的值都是已經被計算的（除了邊界），所以正確性肯定沒問題。

其實看代碼會好理解一點！！

復雜度分析：考慮直接算出每一層遞歸的塊數。

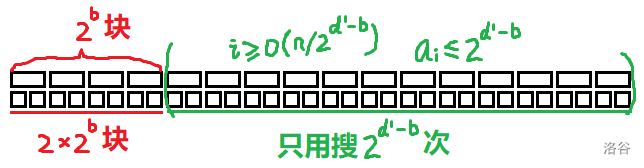
我們考察第 \(d\) 層，記其上一層 \(d^{\prime}=d-1\)。直接放縮復雜度，我們認為第 \(d^{\prime}\) 層全部塊都被遞歸到了：那么顯然塊是均勻分布的，第 \(d^{\prime}\) 層的每一塊長度都是 \(O(n/2^{d^{\prime}})\)。類似其他題解，假設第 \(d^{\prime}\) 層前 \(2^b\) 塊全部都往下遞歸了；那么后面一段應當有 \(i\ge O(2^b\times n/2^{d^{\prime}})=O(n/2^{d^{\prime}-b})\)，故后面一段 \(a_i\le O(2^{d^{\prime}-b})\)。此時看遞歸到第 \(d\) 層的情況，前面 \(2\times2^b\) 塊，后面本質不同塊只有 \(O(2^{d^{\prime}-b})\) 個，于是復雜度為

因此一層的遞歸次數只有 \(O(2^{d/2})\) 次，求和即有

故真正進入的層數是 \(O(\sqrt n)\) 的，每次真正進入都能夠 \(O(n)\) 求出單點值，復雜度即 \(O(n\sqrt n)\)。