[原]SQL解答“A Unique Magic Hexagon”引出的CPU測試
〇〇不知道從哪里搞來了一套極耗腦細(xì)胞的題目：
將1-19這19個自然數(shù)填入圓圈中，使每一直線上的幾個數(shù)之和都相等，請用SQL/PLSQL求解。
其中一個答案如下：
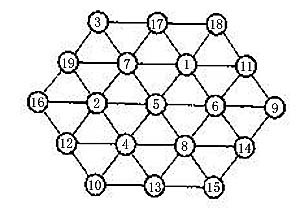想了一晚沒什么好辦法可以投機(jī)取巧，今天早上將題目的所有約束條件放到SQL中，然后閉上眼睛讓Oracle跑：
set linesize 150;
set pagesize 500;
col num format 999 ;
set timing on ;
set autotrace on ;
with points as (
select level num from dual connect by level <= 19
) -- select num from points
select /*+ parallel(dual 4) */
p1.num,p2.num,p3.num,
p4.num,p5.num,p6.num,p7.num,
p8.num,p9.num,p10.num,p11.num,p12.num,
p13.num,p14.num,p15.num,p16.num,
p17.num,p18.num,p19.num
from
points p1,points p2,points p3,
points p4,points p5,points p6,points p7,
points p8,points p9,points p10,points p11,points p12,
points p13,points p14,points p15,points p16,
points p17,points p18,points p19
where
p1.num not in ( p2.num,p3.num,p4.num,p5.num,p6.num,p7.num,p8.num,p9.num,p10.num,p11.num,p12.num,p13.num,p14.num,p15.num,p16.num,p17.num,p18.num,p19.num )
and p2.num not in ( p1.num, p3.num,p4.num,p5.num,p6.num,p7.num,p8.num,p9.num,p10.num,p11.num,p12.num,p13.num,p14.num,p15.num,p16.num,p17.num,p18.num,p19.num )
and p3.num not in ( p1.num,p2.num, p4.num,p5.num,p6.num,p7.num,p8.num,p9.num,p10.num,p11.num,p12.num,p13.num,p14.num,p15.num,p16.num,p17.num,p18.num,p19.num )
and p4.num not in ( p1.num,p2.num,p3.num, p5.num,p6.num,p7.num,p8.num,p9.num,p10.num,p11.num,p12.num,p13.num,p14.num,p15.num,p16.num,p17.num,p18.num,p19.num )
and p5.num not in ( p1.num,p2.num,p3.num,p4.num, p6.num,p7.num,p8.num,p9.num,p10.num,p11.num,p12.num,p13.num,p14.num,p15.num,p16.num,p17.num,p18.num,p19.num )
and p6.num not in ( p1.num,p2.num,p3.num,p4.num,p5.num, p7.num,p8.num,p9.num,p10.num,p11.num,p12.num,p13.num,p14.num,p15.num,p16.num,p17.num,p18.num,p19.num )
and p7.num not in ( p1.num,p2.num,p3.num,p4.num,p5.num,p6.num, p8.num,p9.num,p10.num,p11.num,p12.num,p13.num,p14.num,p15.num,p16.num,p17.num,p18.num,p19.num )
and p8.num not in ( p1.num,p2.num,p3.num,p4.num,p5.num,p6.num,p7.num, p9.num,p10.num,p11.num,p12.num,p13.num,p14.num,p15.num,p16.num,p17.num,p18.num,p19.num )
and p9.num not in ( p1.num,p2.num,p3.num,p4.num,p5.num,p6.num,p7.num,p8.num, p10.num,p11.num,p12.num,p13.num,p14.num,p15.num,p16.num,p17.num,p18.num,p19.num )
and p10.num not in ( p1.num,p2.num,p3.num,p4.num,p5.num,p6.num,p7.num,p8.num,p9.num, p11.num,p12.num,p13.num,p14.num,p15.num,p16.num,p17.num,p18.num,p19.num )
and p11.num not in ( p1.num,p2.num,p3.num,p4.num,p5.num,p6.num,p7.num,p8.num,p9.num,p10.num, p12.num,p13.num,p14.num,p15.num,p16.num,p17.num,p18.num,p19.num )
and p12.num not in ( p1.num,p2.num,p3.num,p4.num,p5.num,p6.num,p7.num,p8.num,p9.num,p10.num,p11.num, p13.num,p14.num,p15.num,p16.num,p17.num,p18.num,p19.num )
and p13.num not in ( p1.num,p2.num,p3.num,p4.num,p5.num,p6.num,p7.num,p8.num,p9.num,p10.num,p11.num,p12.num, p14.num,p15.num,p16.num,p17.num,p18.num,p19.num )
and p14.num not in ( p1.num,p2.num,p3.num,p4.num,p5.num,p6.num,p7.num,p8.num,p9.num,p10.num,p11.num,p12.num,p13.num, p15.num,p16.num,p17.num,p18.num,p19.num )
and p15.num not in ( p1.num,p2.num,p3.num,p4.num,p5.num,p6.num,p7.num,p8.num,p9.num,p10.num,p11.num,p12.num,p13.num,p14.num, p16.num,p17.num,p18.num,p19.num )
and p16.num not in ( p1.num,p2.num,p3.num,p4.num,p5.num,p6.num,p7.num,p8.num,p9.num,p10.num,p11.num,p12.num,p13.num,p14.num,p15.num, p17.num,p18.num,p19.num )
and p17.num not in ( p1.num,p2.num,p3.num,p4.num,p5.num,p6.num,p7.num,p8.num,p9.num,p10.num,p11.num,p12.num,p13.num,p14.num,p15.num,p16.num, p18.num,p19.num )
and p18.num not in ( p1.num,p2.num,p3.num,p4.num,p5.num,p6.num,p7.num,p8.num,p9.num,p10.num,p11.num,p12.num,p13.num,p14.num,p15.num,p16.num,p17.num, p19.num )
and p19.num not in ( p1.num,p2.num,p3.num,p4.num,p5.num,p6.num,p7.num,p8.num,p9.num,p10.num,p11.num,p12.num,p13.num,p14.num,p15.num,p16.num,p17.num,p18.num )
and p1.num +p2.num + p3.num = 38
and p3.num +p7.num + p12.num = 38
and p12.num + p16.num + p19.num = 38
and p17.num + p18.num + p19.num = 38
and p8.num + p13.num + p17.num = 38
and p1.num + p4.num + p8.num = 38
and p2.num + p6.num + p11.num + p16.num = 38
and p4.num + p9.num + p14.num + p18.num = 38
and p2.num + p5.num + p9.num + p13.num = 38
and p7.num + p11.num + p15.num + p18.num = 38
and p4.num + p5.num + p6.num + p7.num = 38
and p13.num + p14.num + p15.num + p16.num = 38
and p1.num + p5.num + p10.num + p15.num + p19.num = 38
and p3.num + p6.num + p10.num + p14.num + p17.num = 38
and p8.num + p9.num + p10.num + p11.num + p12.num = 38
/
NUM NUM NUM NUM NUM NUM NUM NUM NUM NUM NUM NUM NUM NUM NUM NUM NUM NUM NUM ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- 15 13 10 14 8 4 12 9 6 5 2 16 11 1 7 19 18 17 3 15 14 9 13 8 6 11 10 4 5 1 18 12 2 7 17 16 19 3 16 12 10 19 2 4 13 3 7 5 8 15 17 1 6 14 18 11 9 16 19 3 12 2 7 17 10 4 5 1 18 13 8 6 11 15 14 9 18 11 9 17 1 6 14 3 7 5 8 15 19 2 4 13 16 12 10 18 17 3 11 1 7 19 9 6 5 2 16 14 8 4 12 15 13 10 3 17 18 19 7 1 11 16 2 5 6 9 12 4 8 14 10 13 15 3 19 16 17 7 2 12 18 1 5 4 10 11 6 8 13 9 14 15 9 11 18 14 6 1 17 15 8 5 7 3 13 4 2 19 10 12 16 9 14 15 11 6 8 13 18 1 5 4 10 17 7 2 12 3 19 16 10 12 16 13 4 2 19 15 8 5 7 3 14 6 1 17 9 11 18 10 13 15 12 4 8 14 16 2 5 6 9 19 7 1 11 3 17 18 12 rows selected. Elapsed: 00:00:40.15
注：第一行那3個點，從左到右 p1 p2 p3 第二行從左到右 p4 p5 p6 p7 ,如此類推。
我嘗試在Oracle 10g中運(yùn)行這個結(jié)果，可是等了2個小時結(jié)果還是跑不出來，將查詢放在Oracle 11g中幾十秒后就有結(jié)果。
以上結(jié)果是在一臺CPU 是 Intel XEON 2.8GHz 的 DELL PE2850 服務(wù)器上跑得的。突發(fā)好奇拿到一臺CPU 是 Intel XEON 5110 頻率僅有 1.6GHz 的HP DL380 G5 上跑，用時 00:00:30.53 ，頻率高一大截但是成績卻差一大截，這讓我非常驚訝，看老白的《Oracle RAC日記》中提到一個案例也是有類似的情況——頻率高性能反而低。
難道我人品這么好今天就遇到了？
將這個查詢拿到一臺CPU為SPARC 頻率為1.5GHz 的 Sun Fire V890 小型機(jī)上面跑，用時 00:01:05.66。
看來頻率并不是決定性能的絕對參考指標(biāo)，同樣根據(jù)老白的辦法，寫一個冒泡排序的C程序，然后拿到多個平臺上跑一次：
Intel Xeon 2.8GHz 0m33.831s Intel Xeon 3.0GHz 0m31.692s Intel Xeon 5110 1.6GHz 0m31.137s Intel Xeon 5160 3.0GHz 0m18.842s Intel Xeon 5450 3.0GHz 0m16.655s SUN SPARC 1.5GHz 0m42.787s IBM Power5 1.9GHz 0m37.84s
從測試結(jié)果來看，同樣架構(gòu)下頻率越高性能的確越好，但是不同的架構(gòu)即使頻率相同性能孰優(yōu)孰劣還是說不準(zhǔn)。
后來我才知道這條數(shù)學(xué)題叫做“A Unique Magic Hexagon”（Google翻譯：獨特的魔術(shù)六角，有人稱為“六角幻方”），這里有精妙的解答過程絕非我這種暴力方法
浙公網(wǎng)安備 33010602011771號