[OpenGL ES 03]3D變換：模型，視圖，投影與Viewport

本文詳細(xì)介紹 3D 相關(guān)的一些數(shù)學(xué)知識(shí)，如矩陣變換，以及 3D 空間的物體是如何映射到屏幕上去這一整個(gè)過(guò)程：模型變換，視圖變換，投影變換，視口變換。

本文遵循“署名-非商業(yè)用途-保持一致”創(chuàng)作公用協(xié)議

前言

本來(lái)打算直接寫(xiě)教程 04 的，但是想到3D 變換涉及的數(shù)學(xué)知識(shí)較多，往往是很多初學(xué)者的攔路虎（比如我自己）。再加上OpenGL ES 2.0 不再提供OpenGL ES 1.0中 3D 變換相關(guān)的一些重量級(jí)函數(shù)，如 glMatrixMode(GL_PROJECTION); glMatrixMode(GL_MODELVIEW); glLoadMatrixf; glMultMatrix 等，這些函數(shù)在 OpenGL ES 2.0 中均需要我們自己去實(shí)現(xiàn)。如果不對(duì)線性代數(shù)與幾何知識(shí)作一些簡(jiǎn)單介紹，恐怕不少人難以理解文中的一些步驟為什么要那么做。因此今天這一篇文章將放棄原定計(jì)劃，先來(lái)介紹一些 3D 數(shù)學(xué)以及 3D 變換相關(guān)的知識(shí)。BTW，原定計(jì)劃的代碼示例已經(jīng)寫(xiě)好了，有興趣的同學(xué)可以先行瀏覽，代碼放在這里，運(yùn)行效果如下：

OpenGL ES 04 示例

一，3D數(shù)學(xué)歷史

我們都學(xué)過(guò)幾何學(xué)，應(yīng)該都知道歐幾里得（公元前3世紀(jì)希臘數(shù)學(xué)家）這位幾何學(xué)鼻祖，正是這位大牛創(chuàng)建了歐幾里得幾何學(xué)，他提出了基于 X，Y，Z 三軸的三維空間概念。到了17世紀(jì)，又出了位大牛笛卡爾，我們通常所說(shuō)的笛卡爾坐標(biāo)就是他的創(chuàng)造，笛卡爾坐標(biāo)非常完美地將歐幾里得幾何學(xué)理論與代數(shù)學(xué)聯(lián)系到一塊。正是因?yàn)橛辛说芽栕鴺?biāo)，我們才能夠用簡(jiǎn)單的矩陣（Matrix）來(lái)表示三維變換。但用矩陣來(lái)表示三維變換操作有一個(gè)無(wú)法解決的問(wèn)題-萬(wàn)向節(jié)鎖 。什么是萬(wàn)向節(jié)鎖呢？簡(jiǎn)單地說(shuō)就是兩個(gè)軸旋轉(zhuǎn)到同一個(gè)方向上去了，這兩個(gè)軸平行了，因此就比原來(lái)少了一維（詳情可參考這里）。過(guò)了一百多年，漢密爾頓（Sir William Rowan Hamilton）創(chuàng)建了四元數(shù)（quaternion）解決了因?yàn)樾D(zhuǎn)而導(dǎo)致萬(wàn)向節(jié)鎖的問(wèn)題，然后四元數(shù)還有其他用處，但在3D數(shù)學(xué)里主要是用來(lái)處理旋轉(zhuǎn)問(wèn)題。

好吧，或許你看得一頭霧水，不要緊，你只要知道：用矩陣來(lái)表示3D變換，但矩陣在表示旋轉(zhuǎn)時(shí)可能會(huì)導(dǎo)致萬(wàn)向節(jié)鎖的問(wèn)題，而使用四元數(shù)可以避免萬(wàn)向節(jié)鎖就可以了。

二，矩陣變換

在前面提到可使用 Matrix 來(lái)表示三維變換操作，那么變換又是如何通過(guò) Matrix 實(shí)現(xiàn)的呢？下面就來(lái)講這個(gè)。在這里我推薦一本3D數(shù)學(xué)入門(mén)書(shū)籍：《3D數(shù)學(xué)基礎(chǔ)：圖形與游戲開(kāi)發(fā)》

通常我們使用 4 維向量 (x, y, z, w) 表示在3D空間中的一個(gè)點(diǎn)，最后一維 w 表示齊次坐標(biāo)。齊次坐標(biāo)的含義是兩條平行線在投影平面的無(wú)窮遠(yuǎn)處相交于一點(diǎn)，但在 Matrix 中沒(méi)有表示無(wú)窮大，所以增加了齊次坐標(biāo)這一維。你可以想象下，火車(chē)軌道的兩條邊在無(wú)限遠(yuǎn)處看起來(lái)就相交于一點(diǎn)，齊次坐標(biāo)詳細(xì)的介紹可以參考這篇文章。

矩陣運(yùn)算規(guī)則：

1) 若矩陣 A 和 B 不是互逆矩陣，則不滿(mǎn)足乘法交換律，即 A × B 不等于 B × A；
2) M × N 階的矩陣只能和 N × O 階的矩陣相乘，即 N 的階數(shù)相等，結(jié)果為 M × O 階的矩陣；
3) 矩陣 A × B 的運(yùn)算過(guò)程是 A 的每一行依次乘以 B 的每一列作為結(jié)果矩陣中的一行；
4) 矩陣 A 的逆矩陣 B 滿(mǎn)足 A × B = B × A = 單位矩陣。
5) 單位矩陣是對(duì)角線上的值為1，其余均為 0 的矩陣。單位矩陣不影響坐標(biāo)變換（你可以將下面的3D變換矩陣換成單位矩陣來(lái)思考下）。

3D空間的物體投影到2D平面上時(shí)，就需要使用到齊次坐標(biāo)，因此我們需要使用 4 × 4 的 Matrix 來(lái)表示變換。在編程語(yǔ)言中，這樣的 Matrix 可用大小為 16 的一維數(shù)組或4 × 4 的二維數(shù)組來(lái)表示。由于矩陣乘法不滿(mǎn)足乘法交換律，用數(shù)組表示 Matrix 又分為兩種形式：行主序和列主序，它們?cè)诒举|(zhì)上是等價(jià)的，只不過(guò)是一個(gè)是右乘（行主序，矩陣放右邊）和一個(gè)是左乘（列主序，矩陣放左邊）。OpenGL 使用列主序矩陣，即列矩陣，因此我們總是倒過(guò)來(lái)算的（左乘矩陣，變換效果是按從右向左的順序進(jìn)行）：投影矩陣 × 視圖矩陣 × 模型矩陣 × 3D位置。

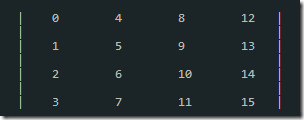
4× 4列矩陣的數(shù)組表示：數(shù)字表示數(shù)組下標(biāo)對(duì)應(yīng)的行列位置：

那么

平移矩陣可表示為：

平移矩陣 × 列矩陣(a, b, c, 1) = 列矩陣(a + x, b + y, c + z, 1)。

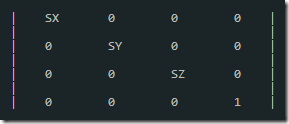
縮放矩陣可表示為：

縮放矩陣 × 列矩陣(a, b, c, 1) = 列矩陣(a × sx, b × sy, c × sz, 1)。

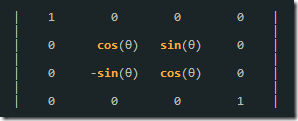
繞 X 軸旋轉(zhuǎn)的旋轉(zhuǎn)矩陣可表示為：

繞 X 軸旋轉(zhuǎn)的旋轉(zhuǎn)矩陣 × 列矩陣(a, b, c, 1) = 列矩陣(a, b × cos(θ) - c × sin(θ), b × -sin(θ) + c × cos(θ), 1)。

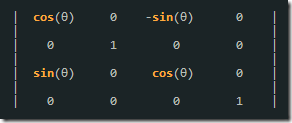
繞 Y 軸旋轉(zhuǎn)的旋轉(zhuǎn)矩陣可表示為：

繞 Y 軸旋轉(zhuǎn)的旋轉(zhuǎn)矩陣 × 列矩陣(a, b, c, 1) = 列矩陣(a × cos(θ) - c × sin(θ), b , a × -sin(θ) + c × cos(θ), 1)。

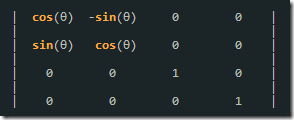
繞 Z 軸旋轉(zhuǎn)的旋轉(zhuǎn)矩陣可表示為：

繞 Z 軸旋轉(zhuǎn)的旋轉(zhuǎn)矩陣 × 列矩陣(a, b, c, 1) = 列矩陣(a × cos(θ) - b × sin(θ), a × -sin(θ) + b × cos(θ), c, 1)。

三，OpenGL 中的實(shí)現(xiàn)

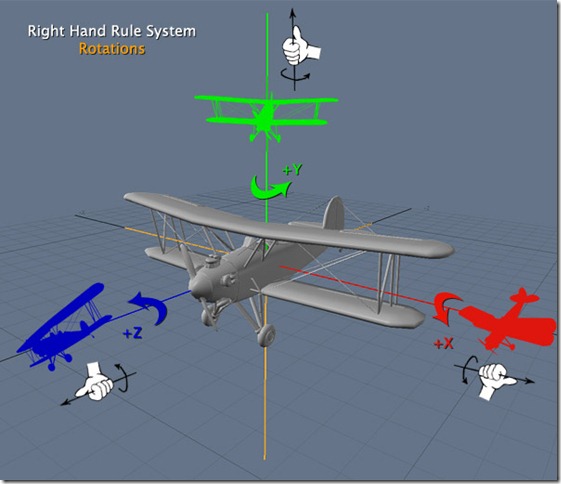
OpenGL 使用右手規(guī)則進(jìn)行旋轉(zhuǎn)，因此逆時(shí)針?lè)较虻倪x擇是正角度的，而順時(shí)針?lè)较虻男D(zhuǎn)是負(fù)角度的。還記得中學(xué)學(xué)物理時(shí)候的右手規(guī)則么？忘記了的話(huà)，看下圖：

注意：

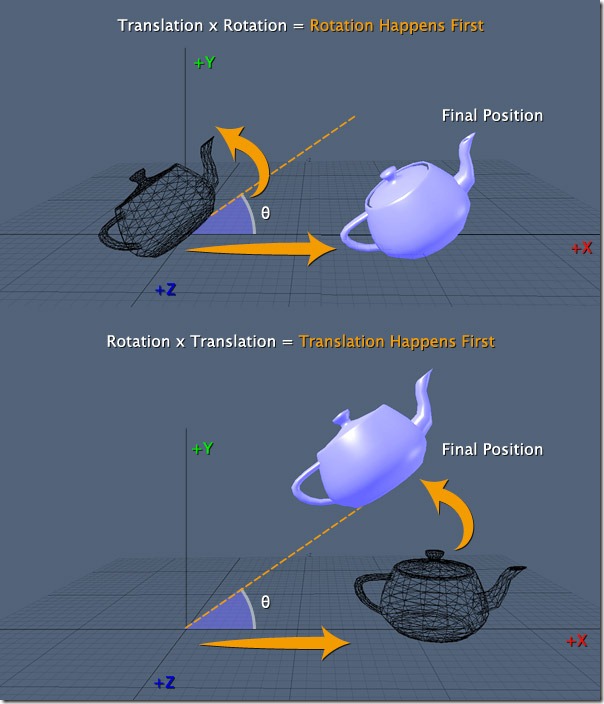
前面說(shuō)到矩陣乘法不滿(mǎn)足乘法交換律，因此你對(duì)一個(gè)3D坐標(biāo)先進(jìn)行旋轉(zhuǎn)，然后進(jìn)行平移（平移矩陣 × 旋轉(zhuǎn)矩陣 × 3D坐標(biāo)）；與先進(jìn)行平移，然后進(jìn)行旋轉(zhuǎn)（旋轉(zhuǎn)矩陣 × 平移矩陣 × 3D坐標(biāo)）得到的效果是大為迥異的。如下圖所示：

在第一種情況下，我們通常稱(chēng)旋轉(zhuǎn)是在 local space 中進(jìn)行，因?yàn)樗抢@著物體自己的中心點(diǎn)進(jìn)行的，而在后一種情況下的旋轉(zhuǎn)通常稱(chēng)為是在 world space 中進(jìn)行的。我們知道點(diǎn)是可以在坐標(biāo)空間之間相互轉(zhuǎn)換的，這是一個(gè)很重要的概念。OpenGL 中物體最初是在本地坐標(biāo)空間中，然后轉(zhuǎn)換到世界坐標(biāo)空間，再到 camera 視圖空間，再到投影空間，這一系列轉(zhuǎn)換都是靠 matrix 計(jì)算來(lái)實(shí)現(xiàn)。

上面的這個(gè)過(guò)程在 OpenGL 及 OpenGL ES 1.0 中，對(duì)應(yīng)的代碼類(lèi)似于：

   glViewport (0, 0, (GLsizei) w, (GLsizei) h);  　　a)
   glMatrixMode (GL_PROJECTION);　　　　　　　　　　　　b)
   glLoadIdentity ();
   glFrustum (-1.0, 1.0, -1.0, 1.0, 1.5, 20.0);　　  c)
   glMatrixMode (GL_MODELVIEW);　　　　　　　　　　　　 d)

   glClear (GL_COLOR_BUFFER_BIT);
   glColor3f (1.0, 1.0, 1.0);
   glLoadIdentity ();             /* clear the matrix */
   /* viewing transformation  */
   gluLookAt (0.0, 0.0, 5.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0);　　　　e)
   glScalef (1.0, 2.0, 1.0);      /* modeling transformation */ 　f)
   glutWireCube (1.0);　　　　　　　　　　　　　　　　　　　　　　　　　 g)
   glFlush ();

說(shuō)明：

a) 是用于viewport（視口）變換，viewport 變換發(fā)生在投影到2D 投影平面之后，該變換是將投影之后歸一化的點(diǎn)映射到屏幕上一塊區(qū)域內(nèi)的坐標(biāo)。視口變換的目的是指定投影之后圖像在屏幕上顯示的區(qū)域。如下示意圖所示：

視口變換 glViewport(x, y, width, height); x,y 是投影平面描繪在屏幕或窗口上的起始位置（注意屏幕坐標(biāo)以左上方為原點(diǎn)），width和height是以像素為單位，指投影平面在屏幕上描繪的區(qū)域大小。如果投影平面的寬高比，與width/height比不相同（如上面的右圖），那么描繪的場(chǎng)景就會(huì)扭曲。

從裁剪到屏幕的整個(gè)過(guò)程如下圖所示，w 就是前面提到的齊次坐標(biāo)那一維，從 Clip Space 到 Normalized Device Space 就是投影規(guī)范化的過(guò)程，從 Normalized Device Space 到 Window Space 就是 viewport 變換過(guò)程。

投影，視口變換過(guò)程

該轉(zhuǎn)換內(nèi)部計(jì)算公式為：

(xw, yw)是屏幕坐標(biāo)，(x, y, width, height)是傳入的參數(shù)，(xnd, ynd)是投影之后經(jīng)歸一化之后的點(diǎn)（上圖中 Normalized Device Space 空間的點(diǎn)）。因此 viewport 變換就是將投影之后歸一化的點(diǎn)轉(zhuǎn)換為真正可用于在屏幕上進(jìn)行渲染的屏幕坐標(biāo)；

b) 是說(shuō)明下面的 matrix 是用于投影變換的，在本例中，是通過(guò)語(yǔ)句 c) glFrustum 來(lái)設(shè)置透視投影變換的。投影變換有兩種：正交投影和透視投影，后面會(huì)有詳細(xì)介紹；

d) 是說(shuō)明下面的 matrix 是用于模型視圖變換，注意，OpenGL 和 OpenGL ES 都將模型變換與視圖變換結(jié)合在一起，而不是分開(kāi)為兩個(gè)，這是因?yàn)槟Ｐ妥儞Q等價(jià)于視圖變換的逆變換。視圖變換是將物體轉(zhuǎn)換到觀察者（一般稱(chēng)之為 camera）的視線空間中。你可以想象一下，照相時(shí)，你可以：A）照相機(jī)不懂，旋轉(zhuǎn)自己的頭找個(gè)側(cè)面像，也可以B）自己不動(dòng)，照相機(jī)旋轉(zhuǎn)一定的角度來(lái)達(dá)到同樣的效果。下面的兩幅圖分別描述了情形A）和情形B）：

情形A）：旋轉(zhuǎn)物體，相機(jī)不動(dòng)

情形B）：旋轉(zhuǎn)相機(jī)，物體不動(dòng)

在 OpenGL 中，我們?cè)谠O(shè)置場(chǎng)景（scene）的時(shí)候通常是采取情形B）的做法，因此在語(yǔ)句 e) 處，我們?cè)O(shè)置相機(jī)的位置和朝向，來(lái)設(shè)定視圖變換，之后的語(yǔ)句 f) glScale 是設(shè)定在模型變換的，最后語(yǔ)句 g) 在本地空間描繪物體。

注意

寫(xiě) OpenGL 代碼時(shí)從前到后的順序依次是：設(shè)定 viewport（視口變換），設(shè)定投影變換，設(shè)定視圖變換，設(shè)定模型變換，在本地坐標(biāo)空間描繪物體。而在前面為了便于理解做介紹時(shí)，說(shuō)的順序是OpenGL 中物體最初是在本地坐標(biāo)空間中，然后轉(zhuǎn)換到世界坐標(biāo)空間，再到 camera 視圖空間，再到投影空間。由于模型變換包括了本地空間變換到世界坐標(biāo)空間，所以我們理解3D 變換是一個(gè)順序，而真正寫(xiě)代碼時(shí)則是以相反的順序進(jìn)行的，如果從左乘矩陣這點(diǎn)上去理解就很容易明白為什么會(huì)是反序的。

有了上面 3D 變換的整體概念，下面來(lái)詳細(xì)說(shuō)說(shuō)投影變換與視圖變換。

四，投影變換

投影變換的目的是確定 3D 空間的物體如何投影到 2D 平面上，從而形成2D圖像，這些 2D 圖像再經(jīng)視口變換就被渲染到屏幕上。前面提到投影變換有兩種：正交投影和透視投影。透視投影用的比較廣泛，它與真實(shí)世界更相近：近處的物體看起來(lái)要比遠(yuǎn)處的物體大；而正交投影沒(méi)有這個(gè)效果，正交投影通常用于CAD或建筑設(shè)計(jì)。下面是正交投影與透視投影效果示意圖：

正交投影	透視投影

透視投影可以通過(guò)兩種方式來(lái)表述，OpenGL 及 OpenGL ES 1.0 提供其中一種： glFrustum，而 glut 輔助庫(kù)提供了另外一種：gluPerspective。它們本質(zhì)上是相同的，只不過(guò)是不同的表述而已：

視錐體/視景體：

glFrustum(left, right, bottom, top, zNear, zFar);

left，right， bootom，top 定義了 near 裁剪面大小，而 zNear 和 zFar 定義了從 Camera/Viewer 到遠(yuǎn)近兩個(gè)裁剪面的距離（注意這兩個(gè)距離都是正值）。由這六個(gè)參數(shù)可以定義出六個(gè)裁剪面構(gòu)成的錐體，這個(gè)錐體通常被稱(chēng)之為視錐體或視景體。只有在這個(gè)錐體內(nèi)的物體才是可以見(jiàn)的，不在這個(gè)錐體內(nèi)的物體就相當(dāng)于不再視線范圍內(nèi)，因而會(huì)被裁減掉，OpenGL 不會(huì)這些物體進(jìn)行渲染。

由于 OpenGL ES 2.0 不提供此函數(shù)，因此我們需要自己實(shí)現(xiàn)該函數(shù)。其計(jì)算公式如下：

假設(shè)：l = left, r = right, b = bottom, t = top, n = zNear, f = zFar，有

透視圖：

gluPerspective(fovy, aspect, zNear, zFar);

fovy 定義了 camera 在 y 方向上的視線角度（介于 0 ~ 180 之間），aspect 定義了近裁剪面的寬高比 aspect = w/h，而 zNear 和 zFar 定義了從 Camera/Viewer 到遠(yuǎn)近兩個(gè)裁剪面的距離（注意這兩個(gè)距離都是正值）。這四個(gè)參數(shù)同樣也定義了一個(gè)視錐體。

在 OpenGL ES 2.0 中，我們也需要自己實(shí)現(xiàn)該函數(shù)。我們可以通過(guò)三角公式 tan(fovy/2) = (h / 2)/zNear 計(jì)算出 h ，然后再根據(jù) w = h * aspect 計(jì)算出 w，這樣就可以得到 left, right, top, bottom, zNear, zFar 六個(gè)參數(shù)，代入在介紹視錐體時(shí)提到的公式即可。

正交投影在 OpenGL 及 OpenGL ES 1.0 中是由 glOrtho 來(lái)提供的，我們可以把正交投影看成是透視投影的特殊形式：即近裁剪面與遠(yuǎn)裁剪面除了Z 位置外完全相同，因此物體始終保持一致的大小，即便是在遠(yuǎn)處看上去也不會(huì)變小。

glOrtho(left, right, bottom, top, zNear, zFar);

left，right， bootom，top 定義了 near 裁剪面大小，而 zNear 和 zFar 定義了從 Camera/Viewer 到遠(yuǎn)近兩個(gè)裁剪面的距離（注意這兩個(gè)距離都是正值）。

假設(shè)：xmax = right, xmin = left, ymax = top, ymin = bottom, zmax = far, zmin = near，正交投影的計(jì)算可分為兩步：首先平移到視錐體的中心，然后縮放。

平移矩陣：（圖中的2min 應(yīng)為 zmin）

縮放矩陣：

正交投影矩陣 R = S × T：

五，視圖變換

視圖變換的目的是為了讓我們能觀察到某個(gè)角度的場(chǎng)景（從觀察者的角度來(lái)說(shuō)）或者說(shuō)是為了將物體從世界坐標(biāo)轉(zhuǎn)換到相機(jī)視線所在視圖空間中來(lái)（從3D物體角度來(lái)說(shuō)）。這可以通過(guò)設(shè)定觀察者的位置和朝向來(lái)實(shí)現(xiàn)的或?qū)ξ矬w進(jìn)行3D變換來(lái)實(shí)現(xiàn)，通常前面一種方式來(lái)實(shí)現(xiàn)（即設(shè)定觀察者的位置與朝向）。如下圖所示，xyz坐標(biāo)軸表示的是世界坐標(biāo)，藍(lán)白色區(qū)域?yàn)橐晥D空間，視圖變換就是要將長(zhǎng)方體從世界空間中轉(zhuǎn)換到視圖空間的坐標(biāo)體系中去，然后再投影規(guī)范化，然后再經(jīng) viewport 轉(zhuǎn)換映射到屏幕上渲染出來(lái)。

視圖變換

在 OpenGL 中，我們可以通過(guò)工具庫(kù)提供的 gluLookAt 這個(gè)函數(shù)來(lái)實(shí)現(xiàn)此功能。該函數(shù)的原型為：

gluLookAt(eyex, eyey, eyez, centerx, centery, centerz, upx, upy, upz);

eye 表示 camera/viewer 的位置， center 表示相機(jī)或眼睛的焦點(diǎn)（它與 eye 共同來(lái)決定 eye 的朝向），而 up 表示 eye 的正上方向，注意 up 只表示方向，與大小無(wú)關(guān)。通過(guò)調(diào)用此函數(shù)，就能夠設(shè)定觀察的場(chǎng)景，在這個(gè)場(chǎng)景中的物體就會(huì)被 OpenGL 處理。在 OpenGL 中，eye 的默認(rèn)位置是在原點(diǎn)，指向 Z 軸的負(fù)方向（屏幕往里），up 方向?yàn)?Y 軸的正方向。在接下來(lái)的教程 04 中，使用的就是這個(gè)默認(rèn)設(shè)置。

OpenGL ES 2.0 也沒(méi)有提供該函數(shù)，glulookat 的內(nèi)部實(shí)現(xiàn)其實(shí)就是先旋轉(zhuǎn)到與觀察者視線相同的方向，然后再平移到觀察者所在的位置。其實(shí)現(xiàn)偽碼如下：

Matrix4 GetLookAtMatrix(Vector3 eye, Vector3 at, Vector3 up){
    Vector3 forward, side;
    forward = at - eye;
    normalize(forward);
    side = cross(forward, up);
    normalize(side);
    up = cross(side, forward);

    Matrix4 res = Matrix4(
                          side.x, up.x, -forward.x, 0,
                          side.y, up.y, -forward.y, 0,
                          side.z, up.z, -forward.z, 0,
                          0, 0, 0, 1);
    translate(res, Vector3(0 - eye));
    return res;
}

上面代碼中的 cross 是叉積，normalize 是規(guī)范化，Matrix4 是列主序，translate 是平移。

六，后記

3D 變換是對(duì)初學(xué)者來(lái)說(shuō)是比較困難的，我盡量寫(xiě)得明白點(diǎn)，但效果如何就不得而知了。寫(xiě)這一篇花了我不少時(shí)間，但對(duì)四元數(shù)和萬(wàn)向節(jié)鎖也只是提及而已，未詳細(xì)介紹，以后再單獨(dú)介紹吧。Nate Robin 寫(xiě)了一個(gè)3D 變換的可視化教程工具，對(duì)于理解投影，視圖，模型變換非常有幫助，強(qiáng)烈建議下載運(yùn)行該程序，并調(diào)整相關(guān)參數(shù)看看效果。下面?zhèn)鲝埥貓D以誘惑你去下載：點(diǎn)此進(jìn)入下載頁(yè)面（Windows 和 Mac 版本都有）