• (A)：獨(dú)立做出來(lái)了，不一定寫(xiě)了。
• [A]：沒(méi)有獨(dú)立做出來(lái)，但是是我犯糖，沒(méi)寫(xiě)。
• A：沒(méi)有獨(dú)立做出來(lái)。
• *：困難的。
• **：難爆了。

ARC070

(C)

貪心，能加則加，如果出現(xiàn)某個(gè) \(+i\) 后 \(>x\) 的話，設(shè)現(xiàn)在與 \(x\) 相差 \(r\)，則可以將 \(+(i-r)\) 的那個(gè)變成 \(+i\)。時(shí)間復(fù)雜度 \(O(\sqrt x)\)。

D

擦，我居然不會(huì)這個(gè) trick。

一個(gè)元素 \(a_i\) 不可能成為不必要的，當(dāng)且僅當(dāng)，去掉這個(gè)元素后，存在一個(gè)和為 \([k-a_i,k-1]\) 的選取方案。

發(fā)現(xiàn)這東西是一個(gè)回退背包，于是直接求方案數(shù)。方案數(shù)比較多，對(duì)一個(gè)大質(zhì)數(shù)取模即可。時(shí)間復(fù)雜度 \(O(nk)\)。

*E

首先有一個(gè)很顯然的 dp，設(shè) \(f_{i,j}\) 表示處理了前 \(i\) 個(gè)矩形，且第 \(i\) 個(gè)矩形的左端點(diǎn)在 \(j\) 的最小代價(jià)。令 \(\text{len}_i=r_i-l_i\)，那么顯然有轉(zhuǎn)移：

發(fā)現(xiàn) \(|j-l_i|\) 是一個(gè)下凸函數(shù)，且前面這個(gè) \(\min\) 是在取滑動(dòng)窗口最小值，歸納一下可以得到 \(f_{i}(j)\) 也是一個(gè)下凸函數(shù)。于是考慮 slope trick。

設(shè)這個(gè)凸函數(shù)上最小值為 \(m\)，且對(duì)應(yīng)的最小值區(qū)間為 \([p,q]\)，則可以可以將上式轉(zhuǎn)化為：

后面這個(gè)式子相當(dāng)于在縮小這個(gè)最小值區(qū)間，即 \([p,q]\) 變成 \([p-\text{len}_i,q+\text{len}_{i-1}]\)。

然后還要加上前面這個(gè)絕對(duì)值函數(shù)，這等價(jià)于將 \((-\infty,l_i]\) 的這些折線斜率整體 \(-1\)，將 \([l_i,+\infty)\) 的折線斜率整體 \(+1\)。然后我們需要維護(hù) \(p,q\)，考慮分討：

• \(p\le l_i\le q\)：此時(shí)最小值只有 \(l_i\) 一個(gè)位置，將 \(l_i\) 左邊的斜率 \(-1\)，右邊的斜率 \(+1\) 即可。
• \(l_i<p\)：\(l_i\) 右側(cè)斜率為 \(-1\) 的段 \([x,y]\)，斜率會(huì)變成 \(0\)，那么新的最小值區(qū)間為 \([\max(x,l_i),y]\)。
• \(l_i>q\)：與上一種同理，新的區(qū)間即為 \([x,\min(y,l_i)]\)。

整個(gè)過(guò)程可以使用兩個(gè)堆分別維護(hù) \(p\) 左側(cè)和 \(q\) 右側(cè)的斜率拐點(diǎn)，每次要找到堆內(nèi)的前兩個(gè)拐點(diǎn)，以及對(duì)整個(gè)堆的橫坐標(biāo)整體偏移，后者打標(biāo)記即可。時(shí)間復(fù)雜度 \(O(n\log n)\)。

F

入門(mén)組初賽考這個(gè)嗎，有意思。

首先如果 \(a\le b\) 那么顯然無(wú)解。

考慮維護(hù)一個(gè)棧，然后遍歷這 \(n\) 個(gè)人，每遍歷到一個(gè)人 \(i\)，我們?cè)儐?wèn)棧頂?shù)娜?\(i\) 是否誠(chéng)實(shí)。如果為否，那么這兩人中至少有一人不誠(chéng)實(shí)，同時(shí)彈出棧即可；否則加入棧。

最終棧從底到頂就是 \(\tt 00\cdots011\cdots1\) 的結(jié)構(gòu)，由于 \(a>b\)，所以棧頂?shù)娜艘欢ㄊ钦\(chéng)實(shí)的。然后拿這個(gè)人一個(gè)一個(gè)問(wèn)即可。故總詢問(wèn)次數(shù)一定不超過(guò) \(2n\)。

ARC101

(C)

顯然最優(yōu)方案的分布是一個(gè)長(zhǎng)度為 \(k\) 的區(qū)間，掃一遍即可。

[D]

考慮正常求中位數(shù)，可以二分答案，將 \(>\text{mid}\) 的變成 \(1\)，將 \(<\text{mid}\) 的變?yōu)?\(-1\)，然后判斷整個(gè)序列的和是否 \(\ge 0\)。

那這個(gè)題就等價(jià)于，是否有一半的子段和 \(\ge 0\)。設(shè) \(s_i\) 為前綴和的話，那么以 \(i\) 結(jié)尾的符合要求的段數(shù)即為 \(\sum\limits_{j=1}^i[s_i-s_{j-1}\ge 0]\)。值域 BIT 做二維偏序即可。

E

有一種容易想到的 dp 是 \(f_{x,i}\) 表示 \(x\) 子樹(shù)內(nèi)還有 \(i\) 個(gè)點(diǎn)需要向外匹配的方案數(shù)，然后可以對(duì)一條邊 \((u,v)\) 枚舉需要匹配的點(diǎn)數(shù) \(i,j\) 和直接匹配的數(shù)量 \(k\) 做轉(zhuǎn)移。但這時(shí)間復(fù)雜度爆干凈了。

考慮容斥。不合法方案相當(dāng)于斷開(kāi)一個(gè)邊集，然后每個(gè)連通塊內(nèi)部匹配。

于是設(shè) \(f_{x,i}\) 表示 \(x\) 子樹(shù)內(nèi)且 \(x\) 所在連通塊大小為 \(i\) 的方案數(shù)。于是有轉(zhuǎn)移：

最后答案即為 \(\sum\limits_{i=1}^n f_{1,i}\cdot i!!\)，時(shí)間復(fù)雜度同樹(shù)上背包，為 \(O(n^2)\)。

F

考慮將向左向右的移動(dòng)，刻畫(huà)為坐標(biāo)系上的向上向右的折線。設(shè) \(i\) 號(hào)點(diǎn)左右離得最近的洞為 \(x_i,y_i\)，那么最終落入的洞就取決于點(diǎn)先碰到 \(x=x_i\) 還是 \(y=y_i\)。

設(shè) \(x'_i=x_i-0.5,y'_i=y_i-0.5\)，如果將所有的 \((x'_i,y'_i)\) 放在平面上，那么在折線右下的 \((x'_i,y'_i)\) 的就表示 \(i\) 號(hào)點(diǎn)落入了左側(cè)的洞，反之左上的就是右側(cè)的洞。

發(fā)現(xiàn)位于右下的 \((x'_i,y'_i)\) 是被折線用唯一一種方式貼著的。于是我們對(duì)著折線 dp，設(shè) \(f_i\) 表示到第 \(i\) 個(gè)點(diǎn)，并且欽定該點(diǎn)被折線貼著的方案數(shù)，于是有轉(zhuǎn)移式子：

BIT 維護(hù)二維偏序即可。

ARC114

(A)

\(50\) 以內(nèi)只有 \(15\) 個(gè)質(zhì)數(shù)，\(2^{15}\) 枚舉質(zhì)數(shù)乘起來(lái)檢驗(yàn)即可。

(B)

顯然只會(huì)選擇若干個(gè)置換環(huán)，于是答案就是 \(2\) 的置換環(huán)個(gè)數(shù)冪次再 \(-1\)。

C

假設(shè)給定了序列。對(duì)于一個(gè)點(diǎn)，如果它和離它最近的跟它相等的點(diǎn)之間的點(diǎn)，權(quán)值都比它們大，那么這兩個(gè)點(diǎn)就可以同時(shí)被操作，可以連邊表示。于是貢獻(xiàn)就是連通塊數(shù)量，可以直接欽定連通塊內(nèi)最左邊的那個(gè)點(diǎn)貢獻(xiàn) \(1\)。

回到原問(wèn)題，考慮用總貢獻(xiàn) \(nm^n\) 減掉每個(gè)點(diǎn)多算的貢獻(xiàn)。對(duì)于點(diǎn) \(i\) 可以枚舉與它相連的點(diǎn) \(j\) 以及權(quán)值 \(k\)，然后容易計(jì)算答案，于是有答案式子：

D

首先有一些容易發(fā)現(xiàn)的事情。

• 一顆棋子只會(huì)朝一個(gè)方向走。
  要是回頭走的話只會(huì)變劣，還不如不走多余的路。
• 棋子之間的移動(dòng)路徑的邊不會(huì)相交。
  對(duì)于兩顆棋子，路徑去掉相交的部分，仍然是分別包含兩顆棋子的路徑，直接這樣走顯然比原先更優(yōu)。

現(xiàn)在這個(gè)問(wèn)題相當(dāng)于是要做 \(n\) 次區(qū)間取反，每個(gè)區(qū)間給定了一側(cè)端點(diǎn)，對(duì)區(qū)間 \([l,r]\) 取反的代價(jià)為 \(r-l\)，問(wèn)最后所有顏色段的端點(diǎn)恰好依次為 \(t_1,t_2,\cdots,t_k\) 的最小代價(jià)。

區(qū)間取反的話可以異或差分一下，就變成了取反兩個(gè)端點(diǎn)。

然后對(duì)于所有 \(a_i\) 我們都可以預(yù)先取反掉，于是我們可以得到剩下的需要被取反的位置 \(b_1,b_2,\cdots,b_m\)。

然后我們就是在做一個(gè)對(duì) \(a_i\) 匹配的操作。對(duì)于一個(gè)初始端點(diǎn) \(a_i\)，我們可以給它匹配一個(gè)最終要匹配的端點(diǎn) \(b_j\)，也可以匹配一個(gè)原先的端點(diǎn) \(a_{i-1}\)。

那這個(gè)顯然可以 dp，升序 \(a,b\) 后，設(shè) \(f_{i,j}\) 表示匹配了 \(a\) 的前 \(i\) 個(gè)、\(b\) 的前 \(j\) 個(gè)的最小代價(jià)。時(shí)間復(fù)雜度 \(O(nm)\)。

無(wú)解的話顯然就是 \(n<m\)。

E

這個(gè)紙張縮小的限制很煩，但實(shí)際上可以轉(zhuǎn)化為：初始橫縱一共 \(H+W-2\) 條直線，隨機(jī)一個(gè)長(zhǎng)度為 \(H+W-2\) 的排列，然后順次切當(dāng)前可以切的直線。

根據(jù)期望的線性性，期望次數(shù)等于每條線被切割的概率之和。

然后對(duì)于極小的可切出矩形，其四側(cè)的直線，由于整體上互不影響，于是可以分開(kāi)考慮。對(duì)于一條直線，如果它排在另外 \(k\) 條之后切，就會(huì)產(chǎn)生 \(\dfrac 1{k+1}\) 的貢獻(xiàn)。于是四側(cè)分別枚舉累加即可。

*F

由于操作后的排列字典序一定不會(huì)小于原排列，于是我們要最大化不變的前綴。

貪心地，我們需要盡可能地劃分前綴，這個(gè)顯然是最長(zhǎng)下降子序列長(zhǎng)度。

然后對(duì)于剩下的一段，我們用值域 BIT 維護(hù)可以劃分的段數(shù)即可。

ARC157

(A)

一個(gè)串形如一段 \(\tt X\) 一段 \(\tt Y\) 的交替，于是 \(\tt XY\) 和 \(\tt YX\) 個(gè)數(shù)相差不會(huì)超過(guò) \(1\)。

同時(shí)，如果同時(shí)存在 \(\tt XX\) 和 \(\tt YY\)，那么一定會(huì)存在 \(\tt XY\) 或 \(\tt YX\)。

這兩個(gè)判掉就可以了。其實(shí)要構(gòu)造也是容易的。

(B)

如果 \(k\) 不大于 \(\tt X\) 的個(gè)數(shù)，那么取出極長(zhǎng) \(\tt X\) 段后按長(zhǎng)度升序貪心改即可。

如果 \(k\) 大于 \(\tt X\) 的個(gè)數(shù)，那么先全部將 \(\tt X\) 改為 \(\tt Y\) 后，將極長(zhǎng)未修改段拿出來(lái)，按長(zhǎng)度降序貪心即可。

[C]

設(shè) \(f_{i,j}\) 表示 \((1,1)\to(i,j)\) 的答案。由于 \((a+1)^2=a^2+2a+1\)，于是可以得到轉(zhuǎn)移式子 \(f_{i,j}=f_{x,y}+g_{x,y}+\binom{x+y-2}{x-1}\)，其中 \(g_{i,j}\) 表示 \((1,1)\to(i,j)\) 的權(quán)值和。\(g\) 的轉(zhuǎn)移顯然是 \(g_{i,j}=g_{x,y}+\binom{x+y-2}{x-1}\)。

D

我怎么卡在了最糖的最后一步。

設(shè) \(\tt Y\) 的個(gè)數(shù)為 \(c\)。首先 \(2\nmid c\) 顯然不合法。

然后設(shè)橫著切成 \(p\) 塊，豎著切成 \(q\) 塊，那么首先要保證 \(pq=\dfrac c2\)。然后對(duì)于每一塊都得是恰好兩個(gè) \(\tt Y\)，相當(dāng)于我們要滿足橫向的 \(\tt Y\) 個(gè)數(shù)和恰好為 \(2q\)，豎著恰好為 \(2p\)。然后我們先貪心分割（能分則分）出來(lái)一種方案，剩下的可以調(diào)整得到，在前綴和上體現(xiàn)為和不變。最后乘起來(lái)即可。

(E)

由于不能出現(xiàn)相鄰 \(\tt Y\)，于是可以得知 \(\tt Y\) 結(jié)點(diǎn)構(gòu)成了一個(gè)獨(dú)立集。

\(\tt YX\) 相當(dāng)于 \(\tt Y\) 不在葉子上，也就是說(shuō)有 \(\dfrac C2\) 個(gè) \(\tt Y\) 不在葉子上。這意味著什么呢，如果根不是 \(\tt Y\)，那么就有 \(B-\dfrac C2\) 個(gè) \(\tt Y\) 在葉子上（根是 \(\tt Y\) 的話 \(+1\) 即可）。

于是我們可以大力 dp。設(shè) \(f_{i,j,0/1}\) 表示以 \(i\) 為根的子樹(shù)中，有 \(j\) 個(gè)葉子是 \(\tt Y\)，并且 \(i\) 是/不是 \(\tt Y\)，此時(shí)可以選出的最多的非葉子的 \(\tt Y\) 的個(gè)數(shù)。然后樹(shù)上背包轉(zhuǎn)移即可。小常數(shù) \(O(n^2)\)。

記得判一堆 corner case，諸如 \(n=1\)，\(2\nmid C\)，\(B<\dfrac C2\) 等等。

**F

考慮 dp。設(shè) \(f_{i,S}\) 表示考慮到 \(s\) 的前 \(i\) 位，且 \(S=t[p+1:i]\)（\(p\) 為 \(t\) 最后一次匹配的位置）時(shí)，字典序最大的答案，然后轉(zhuǎn)移的時(shí)候枚舉是否交換、匹配。

注意這里的狀態(tài)是字典序最大，我們可以再在最高位前面加一個(gè)表示位數(shù)的 \(1\)，這樣求出字典序最大答案后，每一位反轉(zhuǎn)后就是字典序最小的答案。

然而這樣子的時(shí)間復(fù)雜度是 \(O(n2^n)\) 的。

注意到，對(duì)于連續(xù)的三個(gè)位置 \(s[i:i+2],t[i:i+2]\)，通過(guò)枚舉后可以發(fā)現(xiàn)，無(wú)論如何我們都可以使得 \(\operatorname{LCS}(s[i:i+2],t[i:i+2])\ge 2\)。也就是說(shuō)，答案一定不小于 \(2\cdot\left\lfloor\dfrac n3\right\rfloor\)，也就是說(shuō)，我們狀態(tài)中的 \(S\) 只有 \(|S|\le\left\lceil\dfrac n3\right\rceil\) 的是有用的。于是時(shí)間復(fù)雜度變?yōu)?\(O(n2^{\frac n3})\)。

ARC158

(A)

將操作 \(-5\)，就變成了 \(+2,+0,-2\)，可以看作從一個(gè)數(shù)中取一個(gè) \(2\) 到另一個(gè)數(shù)內(nèi)，最終都變成平均數(shù)。于是判奇偶性后相對(duì)順序減一下即可。

B

為什么都有數(shù)學(xué)直覺(jué)啊？？

對(duì)原式變形：

枚舉 \(j\)，那么要最值化這個(gè)式子，\(\dfrac1{x_i},\dfrac1{x_k}\) 只能是最值，維護(hù)前后綴最值即可。

C

為什么都會(huì)這種題啊？？我怎么看了半天都不會(huì)做 /ll。

設(shè) \(w(x,y)\) 表示 \(x+y\) 的進(jìn)位次數(shù)。

于是有 \(f(x+y)=f(x)+f(y)-9\cdot w(x,y)\)。

那么原式就可以轉(zhuǎn)化：

那么只要算 \(\sum\limits_{i=1}^n\sum\limits_{j=1}^nw(a_i,a_j)\) 即可。

咋算呢。若 \(a_i+a_j\ge10^k\)，那么就會(huì)在從低到高第 \(k\) 位發(fā)生一次進(jìn)位。于是枚舉，將取末若干位的 \(a_i\) 排序，對(duì)于一個(gè) \(a_i\) 二分一個(gè)最小的可以進(jìn)位的 \(a_j\) 算貢獻(xiàn)即可。

這題不簡(jiǎn)單吧？？？為什么是綠題？？？

*D

神人題目。

發(fā)現(xiàn)兩側(cè)的齊次多項(xiàng)式次數(shù)差 \(1\)，設(shè)有整數(shù) \(t\) 使得：

兩側(cè)同除以 \(t^{3n+1}\)，可以得到：

也就是說(shuō)如果有一組存在 \(t\) 的 \((x,y,z)\)，那么 \(\left(\dfrac xt,\dfrac yt,\dfrac zt\right)\) 就是答案。

\(p\) 是質(zhì)數(shù)啊，所以看起來(lái)我隨一組出來(lái)不合法的概率也不大的啊。那確實(shí)也不大，按官方題解的說(shuō)法，合法概率大約為 \(\dfrac34\)，期望 \(\dfrac53\) 次就能隨出一組答案。

E

考慮分治。令 \(\text{mid}=\left\lfloor\dfrac{l+r}2\right\rfloor\)。然后我們計(jì)算跨越 \(\text{mid}\) 的點(diǎn)對(duì)的最短路之和。

設(shè) \(f_{i,j,0/1}\) 表示 \((i,j)\) 到 \((\text{mid}+[i>\text{mid}],0/1)\) 的最短路。于是對(duì)于 \((i,x)\) 到 \((j,y)\)（其中 \(l\le i\le\text{mid}<j\le r\)，\(0\le x,y\le 1\)）的最短路，即為 \(\min(f_{i,x,0}+f_{j,y,0},f_{i,x,1}+f_{j,y,1})\)。

那么區(qū)間 \([l,r]\) 的答案可以列出，然后我們推一推式子：

后面那兩個(gè)求和掃一遍就好了，主要還是前面這一坨。

令 \(g_{i,x}=f_{i,x,0}-f_{i,x,1}\)，則前面這坨轉(zhuǎn)化為：

那么我們可以將 \(g_{j,y}\) 排序并預(yù)處理前綴和后，然后枚舉每個(gè) \(g_{i,x}\) 時(shí)，二分出能夠貢獻(xiàn)答案的 \(g_{j,y}\) 的個(gè)數(shù)即可。

時(shí)間復(fù)雜度 \(T(n)=2T\left(\dfrac n2\right)+O(n\log n)\)，即 \(O(n\log^2 n)\)。

**F

這也太難了吧？？？

對(duì)于每一數(shù)位來(lái)說(shuō)，都會(huì)被操作零次或多次，然而這些操作，只有最后一次是對(duì)這個(gè)數(shù)位有用的。因此我們可以直接考慮一個(gè)長(zhǎng)度為 \(k\) 的排列的答案，然后填入這 \(m\) 次操作里面計(jì)算最終答案。假設(shè)已經(jīng)有了前者，那不難發(fā)現(xiàn)后者的系數(shù)就是第二類斯特林?jǐn)?shù)，這個(gè)可以容斥算。

那前者怎么看排列的合法性呢。首先這個(gè) \(b\) 的限制是 \(b_i\) 在 \(b_{i+1}\) 的左邊。

設(shè) \(b_{i,j}\) 表示 \(b_i\) 的十進(jìn)制下從低到高第 \(j\) 位的數(shù)碼。

怎么刻畫(huà)這個(gè)限制呢。首先忽略 \(b_{i,x}=b_{i+1,x}\) 的情況。考慮 \(b_{i,x}\neq b_{i+1,x}\)，將這些 \(x\) 劃分成兩個(gè)集合 \(S_i,T_i\)，使得對(duì)于 \(x\in S_i\)，有 \(b_{i,x}<b_{i+1,x}\)；對(duì)于 \(x\in T_i\)，有 \(b_{i,x}>b_{i+1,x}\)。

那么為了保證 \(b_i\) 與 \(b_{i+1}\) 的相對(duì)順序，我們就需要保證 \(T_i\) 最后出現(xiàn)元素比 \(S_i\) 最后出現(xiàn)的元素要靠前。此外存在一個(gè)特殊情況是，如果 \(b_i\) 和 \(b_{i+1}\) 的相對(duì)順序與他們對(duì)應(yīng)到 \(a\) 內(nèi)的順序不同，那顯然需要做至少一次 \(S_i\) 內(nèi)的操作。

然后 dp。設(shè) \(f_{u}\) 表示當(dāng)前排列后綴構(gòu)成集合為 \(u\) 的合法方案數(shù)。那么向這個(gè)集合中加入的 \(x\) 要滿足 \(\forall x\in T_i,S_i\cap u=\varnothing\)。這個(gè)可以維護(hù) \(S_i\) 的所有超集，然后判斷這些超集里是否存在 \(\overline u\)。高維前綴和即可。

最后統(tǒng)計(jì)答案同樣可以維護(hù)超集。

時(shí)間復(fù)雜度 \(O(n\log n+nk+2^kk^2)\)。

ARC159

(A)

顯然 \(u\to v\) 的最短路徑等于 \((u-1)\bmod n+1\to(v-1)\bmod n+1\) 的最短路徑。Floyd 即可。

(B)

設(shè) \(a=xg,b=yg\)，那么一次操作后就變成 \(a=(x-1)g,b=(y-1)g\)。

\(g\) 只要 \(x\perp y\) 就不會(huì)變。考慮 \(g\) 變了的情況，設(shè)對(duì)同一個(gè) \(g\) 做了 \(k\) 次操作，那么就會(huì)存在一個(gè) \(d\) 滿足 \(d\mid(x-k)\) 和 \(d\mid(y-k)\)，也就是 \(x\equiv y\equiv k\pmod d\)。那顯然我們有 \(d\mid (x-y)\)。于是枚舉 \(x-y\) 的因子可以得到最小的 \(k\)。

時(shí)間復(fù)雜度 \(O(\sqrt n\log n)\)。

[C]

首先找到一些顯然無(wú)解的情況。

最終的序列內(nèi)數(shù)的總和顯然是一個(gè) \(n\) 的倍數(shù)。而我們每次會(huì)將序列總和增加 \(\dfrac{n(n+1)}2\)。若 \(2\nmid n\)，那么一定有 \(n\left\vert\dfrac{n(n+1)}2\right.\)，此時(shí)如果初始總和不是 \(n\) 的倍數(shù)就無(wú)解；若 \(2\mid n\)，那么一定有 \(\left.\dfrac n2\right\vert\dfrac{n(n+1)}2\)，初始總和不是 \(\dfrac n2\) 的倍數(shù)就無(wú)解。

發(fā)現(xiàn)對(duì)于 \(2\mid n\) 時(shí)，只要加入一個(gè)排列，就可以使得總和變成 \(n\) 的倍數(shù)。接下來(lái)考慮如何對(duì)滿足這種條件的序列構(gòu)造。

發(fā)現(xiàn)假設(shè)一次加入 \(\{1,2,3\cdots,n\}\)，一次加入 \(\{n-1,n,n-2,\cdots,1\}\)，兩次相加的總和為 \(\{n,n+2,n+1,\cdots,n+1\}\)，考慮相對(duì)差值，這相當(dāng)于對(duì)一個(gè)數(shù) \(-1\)，一個(gè)數(shù) \(+1\)。于是直接模擬調(diào)整即可，最終必然有解。

(D)

設(shè) \(f_i\) 為以 \(r_i\) 結(jié)尾的 LIS，則顯然有轉(zhuǎn)移式：

值域線段樹(shù)維護(hù)即可。

E

深感到自己是弱智。

首先顯然這是一個(gè)帶權(quán)的二分過(guò)程，由于 \(2\min\{a_i,b_i\}\ge\max\{a_i,b_i\}\)，所以樹(shù)高是 \(\log\) 級(jí)別的。

考慮將這個(gè)二分的過(guò)程變成一棵 BST，即將當(dāng)前區(qū)間 \([l,r]\) 的 \(\text{mid}\) 和 \([l,\text{mid}-1],[\text{mid}+1,r]\) 的 \(\text{mid}_1,\text{mid}_2\) 相連邊。那么 \(x_i\) 就對(duì)應(yīng)到 \(i\) 在樹(shù)上的深度。于是詢問(wèn)就變成了 \([c,d]\) 內(nèi)編號(hào)相鄰的兩個(gè)點(diǎn)的深度差之和。

容易計(jì)算，這東西等于 \([c,d]\cup\text{root}\) 的虛樹(shù)的邊數(shù)和，\(\times2\) 后再減去 \(\text{dep}_l+\text{dep}_r\)。這些東西都可以直接搜。時(shí)間復(fù)雜度 \(O(q\log n)\)。

*F

顯然一個(gè)好的序列當(dāng)且僅當(dāng)不存在絕對(duì)眾數(shù)。

設(shè) \(\operatorname{abmode}(l,r)\) 表示 \(a[l:r]\) 的絕對(duì)眾數(shù)，若不存在，則 \(\operatorname{abmode}(l,r)=0\)。

那么就容易有暴力 dp。設(shè) \(f_i\) 表示前 \(i\) 個(gè)數(shù)的答案，則 \(f_i=\sum\limits_{j=1}^{i-1}[\operatorname{abmode}(2j+1,2i)=0]f_j\)。對(duì)于一個(gè)區(qū)間 \([l,r]\)，其所有子區(qū)間本質(zhì)不同的絕對(duì)眾數(shù)最多只有 \(\log\) 種。考慮枚舉絕對(duì)眾數(shù)，則上式可以變?yōu)椋?/p>

考慮分治。

在區(qū)間 \([l,r]\) 時(shí)，考慮計(jì)算 \(f[l:\text{mid}]\) 對(duì) \(f[\text{mid}+1:r]\) 的貢獻(xiàn)。假設(shè)枚舉了絕對(duì)眾數(shù) \(k\)，那么可以將 \(a_i=k\) 的位置變?yōu)?\(1\)，\(a_i\neq k\) 的位置變?yōu)?\(-1\)，然后在這個(gè)區(qū)間內(nèi)做一個(gè)前綴和，設(shè)為 \(s_{k,i}\)，那么對(duì)于 \(i\in[\text{mid}+1,r]\)，轉(zhuǎn)移式子可以寫(xiě)作：

需要枚舉的 \(k\) 是可以直接預(yù)處理 \([l,\text{mid}]\) 的后綴和 \([\text{mid}+1,r]\) 的前綴。然后后面這個(gè) \(s_{k,i}>s_{k,j}\) 的限制可以 BIT 維護(hù)。這樣子是 \(T(n)=2T\left(\dfrac n2\right)+O(n\log^2n)\) 的，即 \(O(n\log^3n)\)。

然而注意到 \(s_k\) 的值域范圍很小，于是可以直接預(yù)處理一個(gè) \(g_k\) 出來(lái)：

于是時(shí)間復(fù)雜度變?yōu)?\(T(n)=2T\left(\dfrac n2\right)+O(n\log n)\)，即 \(O(n\log^2n)\)。

ARC160

(A)

直接從高位到低位考慮每一位可能的數(shù)即可。

[B]

我發(fā)現(xiàn)我很容易在 arc 的數(shù)學(xué)題犯糖，怎么回事啊……

不妨設(shè) \(x\le y\le z\)，則 \(y^2\le yz\le n\)，故 \(y\le \sqrt n\)。

那么可以枚舉 \(y\)，并且由于有 \(x\in[1,y],z\in\left[y,\dfrac ny\right]\)，并且始終有 \(xz\le n\)，那么這些貢獻(xiàn)都能顯然算出來(lái)。討論一下相等的數(shù)即可。時(shí)間復(fù)雜度 \(O(t\sqrt n)\)。

(C)

設(shè) \(f_{i,j}\) 表示考慮 \(\le i\) 的數(shù)，且當(dāng)前 \(i\) 有 \(j\) 個(gè)的方案數(shù)。顯然可以直接向后轉(zhuǎn)移。這東西看起來(lái)是 \(O(n^2)\) 的，但是有用狀態(tài)很少，只轉(zhuǎn)移有用的狀態(tài)即可。這東西應(yīng)該是 \(O(n)\) 級(jí)別的。

D

顯然 \(k\nmid m\) 時(shí)無(wú)解。

然后倒過(guò)來(lái)，減變成加。考慮是否存在一種操作序列使得可以和一種合法方案一一對(duì)應(yīng)。

由于一個(gè)位置被 \(k\) 次 \(+1\) 等價(jià)于做一次單點(diǎn) \(+k\)。所以可以欽定每個(gè)區(qū)間做不超過(guò) \(k-1\) 次的 \(+1\)。

于是設(shè)一個(gè)操作序列 \(q\)，\(q[1:n-k+1]\) 是對(duì)每個(gè)區(qū)間 \(+1\) 的次數(shù)，\(q[n-k+2:2n-k+1]\) 是對(duì)每個(gè)位置 \(+k\) 的次數(shù)，于是需要滿足：

• \(\sum\limits_{i=1}^{2n-k+1}q_i=\dfrac mk\)。
• \(\forall i\in[1,n-k+1],q_i\in[0,k)\)。

這東西是有上界的插板。考慮容斥，欽定有 \(i\) 個(gè)位置不合法，其他的任意，那么最終答案式子即為：

E

首先顯然每個(gè)葉子都需要被連到。若葉子個(gè)數(shù)為偶數(shù)，那么可以將葉子兩兩連邊，具體的構(gòu)造方案是經(jīng)典的（P4665），即按 \(\text{dfn}\) 升序排列得到葉子 \(a_1,a_2,\cdots,a_k\) 后連接 \(a_x\) 和 \(a_{x+\frac k2}\)。

那奇數(shù)怎么辦呢。考慮枚舉那個(gè)剩下的葉子，手畫(huà)一下可以發(fā)現(xiàn)它可以連接到其祖先的第一個(gè)三度點(diǎn)以外的所有節(jié)點(diǎn)。

于是判掉鏈后取一個(gè)三度點(diǎn)為根節(jié)點(diǎn)開(kāi)始搜即可。

*F

考慮刻畫(huà)排列有序的方式。

將一個(gè)排列 \(p\) 拆分為 \(n\) 個(gè) \(\tt 01\) 序列，第 \(i\) 個(gè)序列 \(a_i\) 滿足 \(a_{i,j}=[p_j\ge i]\)。那么排列有序等價(jià)于對(duì)應(yīng)的 \(\tt 01\) 序列有序。

然后發(fā)現(xiàn) \(a_i\) 順次下來(lái)相當(dāng)于在一個(gè) \(n\) 維空間從 \((0,0,\cdots,0)\) 走到 \((1,1,\cdots,1)\)，于是可以直接做路徑計(jì)數(shù)的 dp。

如果每次修改都要重新 dp 一下那還是很爆，但是你發(fā)現(xiàn)，只有對(duì)答案影響的修改才需要重新 dp。而對(duì)答案有影響的修改 \((x,y)\) 當(dāng)且僅當(dāng)存在一個(gè) \(a_i\) 滿足 \(a_{i,x}>a_{i,y}\)，記錄一下當(dāng)前有哪些 \(\tt 01\) 序列執(zhí)行 \((x,y)\) 的修改是有效的即可。

時(shí)間復(fù)雜度 \(O(2^nn^3)\)。

ARC161

(A)

貪心，升序排序后前一半放奇數(shù)位，后一半放偶數(shù)位，check 一下合法性即可。

(B)

貪心，\(\operatorname{popcount}(n)\ge3\) 則取高三位 \(1\) 即可，否則取 \(n-1\) 或 \(n-3\) 的高三位 \(1\)。

(C)

發(fā)現(xiàn)葉子是唯一確定的，于是從葉子往根做即可。

(D)

首先顯然 \(nd>\dfrac{n(n-1)}2\) 時(shí)無(wú)解。

然后可以直接猜出來(lái)的一個(gè)構(gòu)造是，將 \(x\) 連向 \((x\bmod n)+1\sim((x+d-1)\bmod n)+1\) 就可以了。

證明的話，考慮到，下標(biāo)循環(huán)連續(xù)的 \(k\) 個(gè)點(diǎn)的邊數(shù)肯定是比不連續(xù)的 \(k\) 個(gè)點(diǎn)的邊數(shù)多的，于是只要證明前者合法。發(fā)現(xiàn) \(k\) 變成 \(k+1\) 時(shí)，會(huì)新加入 \(1\) 個(gè)點(diǎn)和 \(\min\{k,d\}\) 條邊。如果每次加入的都是 \(d\) 條邊，那么該導(dǎo)出子圖的密度就恰好是 \(d\)，然而會(huì)出現(xiàn) \(k<d\)，因此一定合法。

**E

這也太變態(tài)了。

首先證明一定有解。

設(shè)初始顏色序列 \(c\in S\) 映射到最終的顏色序列為 \(c'\in T\)。若 \(|S|>|T|\)，那么顯然就會(huì)存在未被映射到的顏色序列。如果這個(gè)成立那么就有解。

\(n<10\) 的情況枚舉可得，下面闡述 \(n\ge 10\) 的情況。

令 \(e(x)\) 表示與點(diǎn) \(x\) 直接相連的點(diǎn)的集合。設(shè)有一個(gè)點(diǎn) \(x\)，\(e(x)=\{u,v,w\}\)，那么有 \(e(u)=\{x,u_1,u_2\},e(v)=\{x,v_1,v_2\},e(w)=\{x,w_1,w_2\}\)。

如果說(shuō) \(c_{u_1}=c_{u_2},c_{v_1}=c_{v_2},c_{w_1}=c_{w_2}\)，那么可以唯一確定 \(c'_u=\lnot c_{u_1},c'_v=\lnot c_{v_1},c'_w=\lnot c_{w_1}\)。這三個(gè)都被唯一確定了，那么 \(c'_x\) 也是唯一確定的。

那么此時(shí)發(fā)現(xiàn)，\(c_x\) 的值不影響 \(c'\)——換句話說(shuō)，這個(gè)時(shí)候至少有 \(2^{n-6}\) 種不同的 \(c\) 對(duì)應(yīng)著相同的 \(c'\)。

也就是說(shuō)，如果我們隨機(jī)一個(gè) \(c\)，那么其無(wú)解的概率 \(\ge\dfrac 1{64}\)。事實(shí)上，根據(jù)官方題解的說(shuō)法，這個(gè)概率大得多（\(\approx0.48\)）。不過(guò)我們估計(jì)的概率已經(jīng)足以證明，我們可以 \(O(1)\) 次隨出一個(gè)合法方案。

那么現(xiàn)在的問(wèn)題就是要如何 check 合法性。

考慮一下，我們的限制形如，設(shè)有節(jié)點(diǎn) \(x\) 以及 \(e(x)=\{u,v,w\}\)，「若 \(c'_x\neq c_u\)，則 \(c'_x=c_v=c_w\)」（輪換同理）。2-SAT 即可。

**F

做 D 的時(shí)候就很好奇 checker 怎么寫(xiě)，怎么放 F 來(lái)了。學(xué)了 mzx\(Purslane\) 大蛇的做法。

首先對(duì)于不連通的情況，抽屜原理可得，一定存在一個(gè)密度 \(\ge d\) 的導(dǎo)出子圖。故直接判掉。

接下來(lái)需要一個(gè)前置內(nèi)容：最大密度子圖問(wèn)題。即如果要求的是 \(|E'|\le d\cdot|V'|\) 的話，我們直接求出 \(\max\{|E'|-d\cdot|V'|\}\)，看是否 \(\le 0\)。

然而本題中，整個(gè)圖就能讓這個(gè)式子 \(=0\)。換句話說(shuō)，我們需要再找到一個(gè)真導(dǎo)出子圖，使得其密度 \(=d\)。

于是問(wèn)題就變成了「最小割是否唯一」，也就是求是否存在一組最小割，它割的不全是連接源（匯）點(diǎn)的邊。

對(duì)于一條邊 \((u,v)\) 能夠被割，當(dāng)且僅當(dāng)，這條邊滿流，并且殘量網(wǎng)絡(luò)不存在 \(u\to v\) 的增廣路。后者相當(dāng)于 \(u,v\) 是否在同一個(gè) SCC 內(nèi)，這兩者是等價(jià)的。于是跑一個(gè) Dinic 和一個(gè) Tarjan 即可。

ARC162

(A)

對(duì)于一對(duì) \((i,j)\ (i<j)\)，若 \(p_i>p_j\)，那么這個(gè)時(shí)候，\(p_i\) 的返程速度一定比 \(p_j\) 快，因此 \(p_j\) 不可能成為冠軍。于是答案就是 \(p\) 不同的后綴最小值個(gè)數(shù)。

(B)

直接找最小數(shù)插到前面即可。如果在最后一個(gè)就拿前面未處理的數(shù)插到后面，這樣肯定不超過(guò) \(2n\) 次。操作不了就是無(wú)解。

(C)

顯然 Bob 一定填 \(k\)，所以如果存在子樹(shù)的 \(\text{mex}\) 恰好為 \(k\)，或者有一個(gè)空缺且存在一個(gè)數(shù)填進(jìn)去后能使 \(\text{mex}\) 為 \(k\)，那么 Alice 必勝，否則 Bob 必勝。

D

哦不，這個(gè)第一步我不會(huì)。我是弱智嗎。

首先對(duì)于一棵 \(n\) 個(gè)點(diǎn)的有標(biāo)號(hào)無(wú)根樹(shù)，如果確定了 \(\deg_i\)，那么可能的無(wú)根樹(shù)數(shù)量即為 \(\dfrac{(n-2)!}{\prod\limits_{i=1}^n(\deg_i-1)!}\)。可以用 Prüfer 序列證。

回到本題，考慮對(duì)每個(gè)節(jié)點(diǎn)算貢獻(xiàn)，那么對(duì)于葉子和根，所有的樹(shù)都是符合要求的，于是它們的貢獻(xiàn)分別都為 \(\dfrac{(n-2)!}{(d_1-1)!\prod\limits_{i=2}^nd_i!}\)。

接下來(lái)考慮一個(gè)非葉子節(jié)點(diǎn) \(x\)。

其子樹(shù)相當(dāng)于還要在 \([x+1,n]\) 中選取一個(gè)子集 \(S\)，并且要求 \(S\cup x\) 構(gòu)成一棵樹(shù)。這個(gè)相當(dāng)于要滿足 \(d_x+\sum\limits_{i\in S}d_i=|S|-1\)。

那么這個(gè)時(shí)候，\(x\) 子樹(shù)內(nèi)的方案數(shù)即為 \(\dfrac{(|S|-1)!}{(d_x-1)!\prod\limits_{i\in S}d_i!}\)。

然后對(duì)于 \(x\) 子樹(shù)外，可以直接將 \(x\) 子樹(shù)并起來(lái)，這樣就相當(dāng)于是這棵樹(shù)的一個(gè)葉子，于是方案數(shù)即為 \(\dfrac{(n-|S|-2)!}{(d_1-1)!\prod\limits_{i\notin S\cup\{x,1\}}d_i!}\)。

這時(shí)的總貢獻(xiàn)即為：

于是考慮 dp。設(shè) \(f_{i,j,k}\) 表示當(dāng)前考慮了 \([i,n]\)，選擇了 \(j\) 個(gè)點(diǎn)，這 \(j\) 個(gè)點(diǎn)的 \(d\) 之和為 \(k\) 的方案數(shù)，轉(zhuǎn)移顯然。然后可以直接拿上式算答案。

時(shí)間復(fù)雜度 \(O(n^3)\)。

*E

不是，這題真的很難吧！！！為什么題解區(qū)都講的這么輕松？？

首先思考如何刻畫(huà)這個(gè)填數(shù)，顯然無(wú)法記錄下具體填了什么。那咋辦。然后我也沒(méi)見(jiàn)過(guò)這種。

設(shè) \(\text{cnt}_i\) 表示 \(i\) 的出現(xiàn)次數(shù)。

注意到（其實(shí)我也不知道大家是怎么注意到的）如果按照 \(\text{cnt}\) 降序去填數(shù)，那么這個(gè)時(shí)候，假設(shè)現(xiàn)在考慮出現(xiàn)次數(shù)為 \(i\) 的數(shù)，如果要讓一個(gè) \(j\) 有 \(\text{cnt}_j=i\)，那么有 \(a_j\ge i\)，并且對(duì)于每個(gè)填入的位置 \(k\) 滿足 \(a_k\ge i\)。

那這樣的話，我們發(fā)現(xiàn)我們無(wú)需關(guān)心每個(gè)位置填了什么，因?yàn)榘凑者@種限制填，更小的 \(\text{cnt}\) 限制更寬，而我們只考慮更緊的限制，從而不產(chǎn)生后效性。

我們只關(guān)心：

• 滿足 \(a_j\ge i\) 的正整數(shù) \(j\) 的個(gè)數(shù) \(c_i\)。
• \(b\) 已經(jīng)被填了多少種數(shù)。
• \(b\) 已經(jīng)被填了多少個(gè)數(shù)。

于是可以 dp。設(shè) \(f_{i,j,k}\) 表示考慮了最終 \(\text{cnt}\ge i\) 的數(shù)，已經(jīng)填入了 \(j\) 種數(shù)、\(k\) 個(gè)數(shù)的方案數(shù)。然后枚舉 \(\text{cnt}=i\) 的數(shù)的個(gè)數(shù) \(x\)。貢獻(xiàn)的系數(shù)即為從未選的 \(c_i-j\) 個(gè)數(shù)中取 \(x\) 出來(lái)，填入 \(c_i-k\) 個(gè)空中，做可重集排列。轉(zhuǎn)移式子即為：

由于 \(j,x\le\dfrac ni\)，所以時(shí)間復(fù)雜度是 \(O(n^3)\) 的。

(F)

我擦，我居然自己做出來(lái)了。

首先當(dāng)然是刻畫(huà)條件，這個(gè) \(A_{a,b}A_{c,d}\le A_{a,d}A_{b,c}\) 的限制等價(jià)于：若 \(A_{a,b}=A_{c,d}=1\ (a<c\land b<d)\)，則 \(A_{a,d}=A_{b,c}=1\)。

繼續(xù)嘗試刻畫(huà)。考慮去掉那些全 \(\tt 0\) 的行列，那么此時(shí)如果 \(A_{a,b}=A_{c,d}=1\)，那么 \((a,b),(c,d)\) 以內(nèi)的矩形就都是 \(\tt 1\)。

那這個(gè)時(shí)候的矩陣滿足什么條件呢。它會(huì)長(zhǎng)成像這樣子：

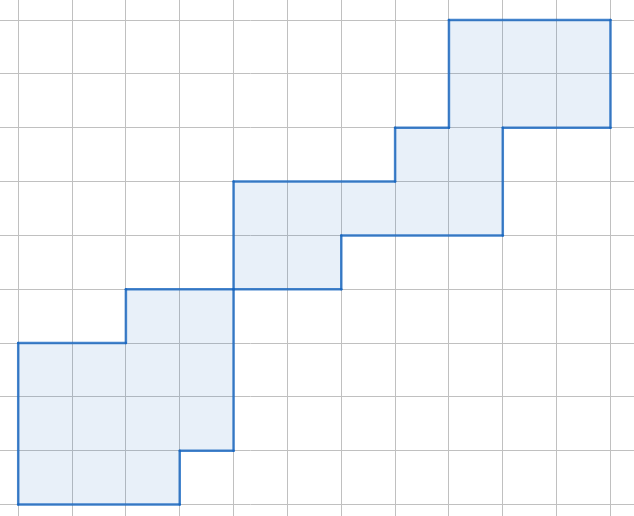
也就是說(shuō)，每行只有一個(gè)連續(xù)段 \([l_i,r_i]\)，并且有 \(l_i\le l_{i-1}\le r_i\le r_{i-1}\)。

那我們可以直接大力 dp 了。設(shè) \(f_{i,j,k}\) 表示考慮了前 \(i\) 行，且 \(l_i=j,r_i=k\) 對(duì)應(yīng)的方案數(shù)。轉(zhuǎn)移式子即為：

顯然直接前綴和優(yōu)化轉(zhuǎn)移可以做到 \(O(n^3)\)。邊界即為 \(f_{1,j,m}=1\)。

然后考慮 \(f_{i,j,k}\) 對(duì)答案的貢獻(xiàn)。現(xiàn)在相當(dāng)于在其中插入 \(n-i\) 個(gè)空行和 \(j-1\) 個(gè)空列，也就是從 \(n\) 行 \(m\) 列中選擇 \(i\) 行 \(m-j+1\) 列出來(lái)，欽定它們非空。那么貢獻(xiàn)即為 \(f_{i,j,k}\cdot\binom ni\cdot\binom m{m-j+1}\)。于是時(shí)間復(fù)雜度依舊為 \(O(n^3)\)。

ARC163

(A)

顯然只需要判能否劃分成兩個(gè)串，枚舉即可。

(B)

顯然只改 \(a_1,a_2\) 是不劣的。將 \(a_{3\sim n}\) 升序排序后枚舉長(zhǎng)度為 \(m\) 并且包含 \([a_1,a_2]\) 的區(qū)間比較即可。

(C)

根據(jù)小學(xué)數(shù)學(xué)可得，因?yàn)?\(\dfrac1{x(x+1)}=\dfrac 1x-\dfrac1{x+1}\)，所以可以構(gòu)造 \(\dfrac 1{1\times2}+\dfrac1{2\times 3}+\dfrac1{3\times4}+\cdots+\dfrac1{(n-1)n}+\dfrac1{n}=1\)。

當(dāng)然這樣可能會(huì)存在一個(gè)正整數(shù) \(k\) 滿足 \(n=k(k+1)\)，這個(gè)時(shí)候咋辦呢，考慮 \(n-1\) 項(xiàng)顯然還是能構(gòu)造的，那么就先有 \(\dfrac 1{1\times2}+\dfrac1{2\times 3}+\dfrac1{3\times4}+\cdots+\dfrac1{(n-2)(n-1)}+\dfrac1{n-1}=1\)，然后我們靈機(jī)一動(dòng)，全體 \(\times\dfrac12\)，然后再加一個(gè) \(\dfrac12\)，于是就是 \(\dfrac 12+\dfrac1{2\times1\times 2}+\dfrac1{2\times2\times 3}+\cdots+\dfrac1{2(n-2)(n-1)}+\dfrac1{2(n-1)}=1\)，就做完了。

不過(guò)這東西 spj 要咋寫(xiě)啊，感覺(jué)不是很好寫(xiě)啊。

D

首先拋出我不會(huì)的引理：

將競(jìng)賽圖中的點(diǎn)集劃分為兩個(gè)可空集合 \(S,T\)，一種劃分是好的當(dāng)且僅當(dāng)對(duì)于 \(\forall x\in S,\forall y\in T\)，存在邊 \(x\to y\)。則好的劃分的個(gè)數(shù)等于競(jìng)賽圖內(nèi) SCC 個(gè)數(shù) \(+1\)。

證明：

將競(jìng)賽圖縮點(diǎn)，這樣可以得到一條廣義鏈 \(a_1,a_2,\cdots,a_n\)。若存在一個(gè) \(i\in[1,n)\)，滿足 \(a_i\in T,a_{i+1}\in S\)，那么這時(shí)因?yàn)橛羞?\(a_{i+1}\to a_i\)，故不合法。

也就是說(shuō)，一種好的劃分只能是找到一個(gè) \(k\in[0,n]\)，令 \(S=\{a_i\mid i\in[1,k]\},T=\{a_i\mid i\in[k+1,n]\}\)。這樣一個(gè) \(k\) 和一組劃分方案一一對(duì)應(yīng)，共有 \(n+1\) 種，減去 \(1\) 后即為 \(n\)，也就是圖內(nèi)的 SCC 個(gè)數(shù)。

這個(gè)刻畫(huà)其實(shí)看起來(lái)還是相當(dāng)顯然的，那這個(gè)能怎么用呢。

我們現(xiàn)在就相當(dāng)于在對(duì)劃分方案計(jì)數(shù)了。于是 dp，設(shè) \(f_{i,j,k}\) 表示考慮了編號(hào)為 \(1\sim i+j\) 的點(diǎn)，其中 \(i=|S|,j=|T|\)，已經(jīng)有 \(k\) 條邊 \((u,v)\) 滿足 \(u<v\)，對(duì)應(yīng)的劃分方案數(shù)。

向后轉(zhuǎn)移，現(xiàn)在新加入一個(gè)點(diǎn) \(p=i+j+1\)。

• 如果 \(p\in S\)，那么它必須連向 \(T\) 內(nèi)的所有點(diǎn)（并且這些邊不滿足 \(u<v\)），然后對(duì)于 \(S\) 內(nèi)的連邊是任意的，設(shè)有 \(x\) 條邊滿足 \(u<v\)，則有轉(zhuǎn)移式：

  \[f_{i+1,j,k+x}\stackrel+\gets f_{i,j,k}\cdot\binom ix \]

• 如果 \(p\in T\)，那么 \(S\) 內(nèi)的所有點(diǎn)必須連向它（并且這些邊都滿足 \(u<v\)），然后對(duì)于 \(T\) 內(nèi)的連邊是任意的，設(shè)有 \(x\) 條邊滿足 \(u<v\)，則有轉(zhuǎn)移式：

  \[f_{i,j+1,k+i+x}\stackrel+\gets f_{i,j,k}\cdot\binom jx \]

最終答案即為 \(\left(\sum\limits_{i=0}^nf_{i,n-i,m}\right)-\binom{\binom n2}m\\\)，后面這個(gè)減是因?yàn)橛梢砜傻梦覀兊霓D(zhuǎn)換求解之間差 \(1\)，而每種競(jìng)賽圖又都會(huì)各多貢獻(xiàn) \(1\)，于是減去競(jìng)賽圖個(gè)數(shù)即可。時(shí)間復(fù)雜度 \(O(n^3m)\)。

**E

這是題？？？

首先考慮 \(n=2\) 的情況。然后你大力打個(gè)表：

大力觀察一下：

哇是分形！

然后你注意到（？），對(duì)于 \(n=2\) 時(shí)，先手必勝當(dāng)且僅當(dāng)四進(jìn)制下存在一個(gè)數(shù)位恰好只有一個(gè)非零數(shù)碼。然后這東西可以直接拓展到 \(n>2\) 的情況。

證明嗎，這個(gè)我不太會(huì)。官方題解應(yīng)該有說(shuō)明，洛谷題解區(qū)也有，感興趣的看下吧。主要是這東西價(jià)值感覺(jué)不是太大。

**F [未做]

不會(huì) poly，再說(shuō)吧。

ARC164

(A)

轉(zhuǎn)三進(jìn)制，個(gè)數(shù)少就拆，判一下即可。

(B)

容易發(fā)現(xiàn)合法當(dāng)且僅當(dāng)存在一個(gè)只有一條同色邊的奇環(huán)，于是保留異色邊，枚舉同色邊，判是否在同一連通塊，并查集即可。

[C]

哦不，我怎么不會(huì)貪心。那我來(lái)嚴(yán)肅學(xué)一下 @TernaryTree 的線性做法吧。

考慮 Bob 選擇的牌初始所在的面，設(shè)目前還需要選 \(x+y\) 個(gè)數(shù)，且有 \(x\) 個(gè)初始在紅色面、\(y\) 個(gè)初始在藍(lán)色面。當(dāng) Alice 操作一次時(shí)，\(x\) 會(huì) \(\pm1\)，然后 Bob 取走一張牌后 \(x\) 相較于 Alice 操作前，要么不變要么 \(-2\)。也就是說(shuō) \(x\) 奇偶性始終不變。

考慮如果 \(x\) 初始是奇數(shù)，那么 Alice 可以操作一下就使得方案不成立了。

于是最終答案相當(dāng)于是在 \(a\) 中取偶數(shù)個(gè)，剩下的取 \(b\) 的最大值。

f然后直接 dp。設(shè) \(f_{i,0/1}\) 表示前 \(i\) 個(gè)數(shù)取了偶/奇數(shù)個(gè) \(a\) 的最大值，于是有轉(zhuǎn)移式子：

時(shí)間復(fù)雜度 \(O(n)\)。

D

哦不，我真是弱智吧，這種題不會(huì)么。

下文所說(shuō)的「和」都是指正電荷數(shù)減去負(fù)電荷數(shù)。

首先觀察，一個(gè)電荷的移動(dòng)方向是兩側(cè)的正負(fù)電荷之和的差決定的。而如果一個(gè)電荷一側(cè)的一對(duì)正負(fù)電荷相撞后消失，則不會(huì)影響這一側(cè)的和。也就是說(shuō)，電荷自始至終的移動(dòng)方向都不變。

然后可以直接大力 dp。設(shè) \(f_{i,j}\) 表示對(duì)于前 \(i\) 個(gè)電荷，和為 \(j\) 的方案數(shù)，那么顯然有轉(zhuǎn)移：

然后設(shè) \(g_{i,j}\) 表示對(duì)于前 \(i\) 個(gè)電荷，和為 \(j\) 的所有方案的總移動(dòng)距離。

考慮貢獻(xiàn)。當(dāng)前最后會(huì)有 \(|j|\) 個(gè)電荷未消失，然后我們每向后考慮一位就會(huì)多移動(dòng)一個(gè)單位，于是貢獻(xiàn)即為 \(f_{i,j}\cdot|j|\)。故轉(zhuǎn)移式子為：

最終答案即為 \(g_{2n,0}\)。時(shí)間復(fù)雜度 \(O(n^2)\)。

E

首先，如果有詢問(wèn)區(qū)間 \([l,r]\)，那么搜索樹(shù)上在這個(gè)區(qū)間兩側(cè)必然有斷點(diǎn)。這樣找出所有斷點(diǎn)，將 \([1,n]\) 切割成 \(k\) 個(gè)區(qū)間。由于第 \(i\) 層最多有 \(2^{i-1}\) 個(gè)節(jié)點(diǎn)，所以搜到的最淺深度 \(d\) 就滿足 \(2^d\ge k\)，于是 \(d_\min=\lceil\log k\rceil\)。

接下來(lái)考慮最小化 \(c\)。

對(duì)于這層所有切割出的區(qū)間，我們有兩種決策：

• 將區(qū)間向上放一層，這樣沒(méi)有貢獻(xiàn)。
• 將這個(gè)區(qū)間和前一個(gè)區(qū)間合并成一個(gè) \([l,r]\)，并上放一層。那么此時(shí)，對(duì)于所有被 \([l,r]\) 包含的詢問(wèn)區(qū)間，都會(huì)產(chǎn)生 \(2\) 的貢獻(xiàn)。貢獻(xiàn)的計(jì)算，考慮枚舉斷點(diǎn)，統(tǒng)計(jì)左、右端點(diǎn)是該斷點(diǎn)的詢問(wèn)區(qū)間數(shù)即可。

于是有 dp，設(shè) \(f_{i,j}\) 表示考慮斷點(diǎn)切割的第 \(i\) 個(gè)區(qū)間，且上一層有 \(j\) 個(gè)區(qū)間產(chǎn)生了貢獻(xiàn)的答案。轉(zhuǎn)移為：

其中 \(w(i)\) 表示第 \(i\) 個(gè)斷點(diǎn)產(chǎn)生的貢獻(xiàn)。

時(shí)間復(fù)雜度 \(O(n^2+q)\)。

*F

由于最后每個(gè)節(jié)點(diǎn)都需要放置一個(gè)棋子，所以每個(gè)節(jié)點(diǎn)上的棋子被翻轉(zhuǎn)的次數(shù)相同。雙方放的棋子顏色又是定的，然后再進(jìn)行轉(zhuǎn)化（這是容易的），可以得到，雙方相當(dāng)于都是要盡可能少地取奇數(shù)深度的節(jié)點(diǎn)。

那這個(gè)相當(dāng)于一個(gè)在刪葉子的過(guò)程。現(xiàn)在輪到某一方，則它必然會(huì)考慮：

• 如果存在偶數(shù)深度的葉子，就刪這個(gè)。
• 如果不存在，那么不得不刪奇數(shù)深度的葉子。在這個(gè)過(guò)程下：
  • 如果某個(gè)葉子是其父親的唯一一個(gè)兒子，那么刪掉這個(gè)葉子后對(duì)方就又能刪去一個(gè)偶數(shù)深度的兒子，對(duì)自己來(lái)說(shuō)是劣的。因此會(huì)先刪父親的兒子數(shù)量 \(>1\) 的葉子。
  • 這樣最后就剩下一堆兒子唯一的父親的葉子。那這時(shí)為了不再變劣，則需要找到一個(gè)離某一個(gè)兒子數(shù) \(>1\) 的祖先最近的葉子，然后這樣刪去。

直接模擬這個(gè)過(guò)程是 \(O(n^2)\) 的，考慮優(yōu)化。

首先，某一方出現(xiàn)第二種情況時(shí)，當(dāng)然希望盡快操作結(jié)束，因此可以考慮成這樣一個(gè)不劣的策略：找到一個(gè)最小的子樹(shù)，滿足其父親為兒子數(shù) \(>1\) 的偶數(shù)深度節(jié)點(diǎn)。將這個(gè)子樹(shù)操作完后，先后手相當(dāng)于進(jìn)行了互換。

事實(shí)上，這個(gè)操作等價(jià)于，取出樹(shù)上的一個(gè)最小的合法的簇并刪去。于是 dfs 一下劃分樹(shù)的簇即可。時(shí)間復(fù)雜度 \(O(n\log n)\)。

ARC165

(A)

等價(jià)于是否存在兩個(gè)不同的質(zhì)因子，如果要構(gòu)造的話可以放在序列里后，一直放 \(1\) 來(lái)補(bǔ)。

[B]

想了一半犯糖了。

顯然修改后不會(huì)讓字典序變大，因此我們肯定盡量保留原序列內(nèi)數(shù)的順序，而這當(dāng)然是我們選擇的一個(gè)前綴。

首先欽定我們選擇了 \([n-k+1,n]\) 這個(gè)區(qū)間，設(shè)我們最終選擇 \([l,r]\) 這個(gè)區(qū)間（顯然 \(l\le n-k+1\)，\(r\le n\)），那么一定有 \([l,n-k]\) 中的所有數(shù)都小于 \([n-k+1,r]\) 中的數(shù)，而且 \([l,n-k]\) 當(dāng)然是升序的。那這樣子我們向前盡可能滑動(dòng)區(qū)間即可，過(guò)程可以用 set 維護(hù)。可以把存在長(zhǎng)度 \(\ge k\) 的遞增區(qū)間的情況特判掉。

[C]

我靠，我真是弱智吧，這種水平怎么打偶愛(ài)。

顯然要二分答案，設(shè)當(dāng)前 check 的是 \(w\)。然后由于是黑白染色，對(duì)于一組邊 \((x,y,w_1),(y,z,w_2)\)，若 \(w_1+w_2<w\)，那么枚舉一下即可得到，此時(shí)一定無(wú)解。

判掉這個(gè)后，你就發(fā)現(xiàn)所有長(zhǎng)度 \(>2\) 的路徑也一定是合法的，于是只要看每條邊，那這個(gè)可以保留所有邊權(quán) \(<w\) 的邊，做一遍黑白染色后，判斷是否為二分圖即可。

D

我覺(jué)得這題挺好的。

首先判掉 \(a_i=c_i\) 的情況。接下來(lái)，貪心地想，我們一定希望一個(gè)約束盡量靠前地滿足，這樣留給后面的自由度更高。這樣就可以連邊，\(a_i\to c_i\) 表示要求 \(x_{a_i}\le x_{c_i}\)。

然后考慮這個(gè)建出來(lái)的圖。我們可以針對(duì) SCC 看。SCC 內(nèi)的點(diǎn)必須相同，然后將 SCC 縮起來(lái)后，可以按照拓?fù)湫蚪o序列 \(x\) 賦值。

因此，對(duì)于一個(gè)約束 \((a_i,c_i)\)，如果 \(a_i,c_i\) 不在同一 SCC 就一定合法；如果在同一 SCC，那么這時(shí)有 \(x_{a_i}=x_{c_i}\)，只能向后找，于是在這個(gè)圖的基礎(chǔ)上同時(shí)連所有需要連的邊 \((a_i+1)\to(c_i+1)\)，繼續(xù)跑 SCC，直到到達(dá)限制區(qū)間的邊界。

這樣時(shí)間復(fù)雜度就是 \(O((n+m)n)\)。

*E

由于多次操作一個(gè)點(diǎn)是沒(méi)有意義的，于是和 ARC158F 的第一步類似，我們可以將操作過(guò)程這么刻畫(huà)：生成一個(gè)排列出來(lái)，然后按照排列依次看這個(gè)點(diǎn)，如果所在連通塊大小 \(>k\) 就刪，否則不管。那么原問(wèn)題的答案，就是這個(gè)排列上被操作的點(diǎn)的個(gè)數(shù)的期望。

考慮一個(gè)以 \(x\) 為根的連通塊，大小為 \(i\)，如果說(shuō)這樣一個(gè)連通塊會(huì)產(chǎn)生，那么和該塊相鄰的 \(j\) 個(gè)點(diǎn)都需要在 \(x\) 之前刪掉。這 \(i+j\) 個(gè)點(diǎn)以外的點(diǎn)都沒(méi)有影響。那么對(duì)于這些點(diǎn)，總共有 \((i+j)!\) 種排列，而 \(j\) 個(gè)點(diǎn)先刪的有 \(i!j!\) 種，故概率為 \(\dfrac{i!j!}{(i+j)!}=\dfrac1{\binom{i+j}{j}}\)。

于是考慮 dp，設(shè) \(f_{u,i,j}\) 表示以 \(u\) 為根的連通塊大小為 \(i\)，與之相鄰的有 \(j\) 個(gè)點(diǎn)的連通塊數(shù)。這里為了方便操作，\(j\) 是不考慮 \(u\) 的父親的，于是可以樹(shù)上背包轉(zhuǎn)移。設(shè) \(u\) 的兒子為 \(v\)，對(duì)應(yīng)枚舉的大小和相鄰點(diǎn)數(shù)為 \(x,y\)，則有：

初值 \(f_{u,1,0}=1\)。由于 \(u\) 不選任何兒子也是會(huì)有相鄰點(diǎn)的，于是還有 \(f_{v,0,1}=1\)。

最終計(jì)算的答案，就是將所有的連通塊產(chǎn)生的貢獻(xiàn)加起來(lái)，即：

里面有個(gè) \([i\neq 1]\) 是在特判前面沒(méi)考慮的父親。

F

首先考慮兩個(gè)數(shù) \(i,j\) 的兩個(gè)端點(diǎn) \((l_i,r_i),(l_j,r_j)\) 的分布情況：

• \(l_i<r_i<l_j<r_j\)：此時(shí)當(dāng)然不會(huì)改變他們?cè)谧罱K序列中的相對(duì)順序，否則肯定變劣。
• \(l_i<l_j<r_i<r_j\)：此時(shí)將 \(i\) 排在前面當(dāng)然是比 \(j\) 排在前面更優(yōu)的。
• \(l_i<l_j<r_j<r_i\)：此時(shí)要么將 \(l_i\) 移到 \(r_j\) 右側(cè)，要么將 \(r_i\) 移到 \(l_j\) 左側(cè)，二者是等價(jià)的，所以兩種順序都可以。

綜上的話，只有前兩種可以確定 \(i,j\) 在最終答案中的順序，滿足的條件即為 \(l_i<l_j\land r_i<r_j\)。連邊 \(i\to j\) 表示 \(i\) 必須排在 \(j\) 前面，那么這樣直接跑最小拓?fù)湫蚣纯伞?/p>

然而這樣的連邊是 \(O(n^2)\) 的，考慮優(yōu)化連邊。

首先將所有二元組端點(diǎn)按 \(l_i\) 升序排列。然后考慮分治，\(\text{sol}(x,y)\) 表示對(duì)下標(biāo)在 \([x,y]\) 的點(diǎn)連邊。先向下遞歸 \(\text{sol}(x,\text{mid}),\text{sol}(\text{mid}+1,r)\)，完成他們內(nèi)部的連邊。然后考慮跨越 \(\text{mid}\) 的要如何處理。由于最初已經(jīng)按照 \(l_i\) 排序，那么 \(l_i<l_j\) 的要求已經(jīng)滿足，只需要考慮 \(r_i<r_j\) 的約束。

如果將 \([\text{mid}+1,r]\) 按照 \(r_i\) 升序，那么每枚舉一個(gè) \(i\in[l,\text{mid}]\)，就只需要對(duì)一個(gè) \([\text{mid}+1,r]\) 的后綴連邊。建立一個(gè)虛點(diǎn)連邊即可。至于按照 \(r_i\) 升序，是可以直接歸并排序的，并且 \([l,\text{mid}]\) 的順序不影響連邊。

這樣這個(gè)圖的邊數(shù)就降到了 \(O(n\log n)\) 級(jí)別。最后再在這個(gè)圖上做拓?fù)渑判蚣纯伞Ｗ⒁庥捎谝钚』值湫颍覀冃枰獌?yōu)先拓展虛點(diǎn)，來(lái)盡可能地得到編號(hào)更小的點(diǎn)。時(shí)間復(fù)雜度 \(O(n\log n)\)。

ARC166

(A)

按照 \(Y\) 的 \(\tt C\) 分段，看每一段 \(\tt A,B\) 個(gè)數(shù)能否相同即可。

(B)

對(duì)每個(gè) \(a_i\) 求一下成為 \(a,b,c,ab,bc,abc\) 倍數(shù)的最小代價(jià)，然后枚舉幾個(gè)代價(jià)較小的取最優(yōu)即可。

(C)

一種標(biāo)記結(jié)果唯一對(duì)應(yīng)一種標(biāo)記方案。考慮斜向拆出 \(\tt LULULU\cdots\) 的折線出來(lái)，然后可以 dp 一下。以一對(duì) \(\tt LU\) 為一組，并且對(duì)應(yīng)一個(gè)正方形，設(shè) \(f_{i,0/1/2}\) 表示考慮了前 \(i\) 組，第 \(i\) 組被標(biāo)記情況是未標(biāo)記 / 標(biāo)記 \(\tt LU\) / 標(biāo)記第 \(i\) 組的 \(\tt D\) 和第 \(i+1\) 組的 \(\tt R\)，然后可以簡(jiǎn)單轉(zhuǎn)移：

對(duì)于矩形拆出的折線，可以分為三部分，左上和右下的等腰直角三角形的部分都是一個(gè) \(f_{i,0}+f_{i,1}\) 的前綴積。中間的平行四邊形是一個(gè) \(f_{\min(h,w),0}+f_{\min(h,w),1}+f_{\min(h,w),2}\) 的冪次。時(shí)間復(fù)雜度 \(O(n+T\log V)\)。

D

降智了。

問(wèn)題相當(dāng)于是每次選擇一個(gè)值域區(qū)間 \([l,r]\)，對(duì) \(x_i\in[l,r]\) 的位置做區(qū)間 \(-1\)，然后問(wèn)全部清零時(shí) \(r-l\) 最小值的最大值。差分一下得到 \(x'_i\)，就變成選擇一對(duì)下標(biāo)區(qū)間 \([l,r]\ (1\le l<r\le n)\)，執(zhí)行 \(x'_l\gets x'_l-1,x'_{r+1}\gets x'_{r+1}+1\)。最后清零時(shí)所有操作的區(qū)間最小的最大值。

這個(gè)看著很能二分啊，但是我做了好久做不了啊。但是這可以直接貪。從左往右掃，對(duì)于一個(gè) \(x'_i>0\)，往后找盡可能近的 \(x'_j<0\) 去消，因?yàn)檫@次不消的話后面消只會(huì)讓操作的區(qū)間更短。這樣就對(duì)了。時(shí)間復(fù)雜度 \(O(n)\)。

**E [未做]

我不會(huì)類歐。

**F [未做]

我不會(huì)數(shù)學(xué)分析。

ARC167

(A)

可以簡(jiǎn)單計(jì)算得到，假設(shè)有四個(gè) \(a,b,c,d\) 滿足 \(a<b<c<d\)，需要兩兩匹配，則分成 \(a+d\) 和 \(b+c\) 一定最優(yōu)。于是將原序列升序后將前 \(2(n-m)\) 個(gè)數(shù)首尾匹配即可。

[B]

若 \(A^B\) 不是完全平方數(shù)，那么存在一個(gè)因數(shù) \(x\) 時(shí)必然存在一個(gè)不同的因數(shù) \(\dfrac{A^B}{x}\)，這樣一對(duì)給答案貢獻(xiàn)了 \(B\)。于是答案即為 \(B\cdot\dfrac{d(A^B)}2\)。

若 \(A^B\) 不是完全平方數(shù)，即此時(shí) \(A\) 為完全平方數(shù)或 \(B\) 為偶數(shù)，那么 \(\sqrt{A^B}\) 會(huì)再貢獻(xiàn)一個(gè) \(\left\lfloor\dfrac B2\right\rfloor\)。

于是時(shí)間復(fù)雜度 \(O(\sqrt A)\)，瓶頸在分解質(zhì)因數(shù)。

C

數(shù)數(shù)真難吧。參考了 @min_inf 的做法。

首先重排 \(a_i\) 顯然不影響答案。考慮對(duì)每個(gè) \(a_i\) 算貢獻(xiàn)。對(duì)于一個(gè)排列算 MST 的過(guò)程，即為從小到大枚舉 \(a_i\)，然后將 \([i-k,i+k]\) 內(nèi)的所有連通塊跟 \(i\) 連邊，分別貢獻(xiàn)一個(gè) \(a_i\)。

有多少連通塊會(huì)和 \(i\) 連邊？容易發(fā)現(xiàn) \(i\) 左右側(cè)各至多一個(gè)。證明考慮欽定和 \(i\) 連邊的是連通塊內(nèi)的最小數(shù)，如果一側(cè)存在兩個(gè)，那么這兩個(gè)連通塊內(nèi)必然存在分別存在一個(gè) \(<a_i\) 的數(shù)，而這兩個(gè)數(shù)之間的距離 \(<k\)，理論上先前應(yīng)該連過(guò)，自然不合法。假設(shè)升序排列了 \(a_i\)，當(dāng)前考慮到 \(a_i\)。設(shè) \(l=\max(1,i-k),r=\min(n,i+k)\)，討論 \(i\) 兩側(cè)連通塊數(shù)量：

• \(0\) 個(gè)連通塊：那么這時(shí)區(qū)間內(nèi)的數(shù)都 \(\ge a_i\)，于是相當(dāng)于要在 \(a_{[i+1,n]}\) 中選 \(r-l\) 個(gè)數(shù)填滿這個(gè)區(qū)間，方案數(shù)為 \(\binom{n-i}{r-l}(r-l)!(n-r+l-1)!\)。
• \(1\) 個(gè)連通塊：這個(gè)直接算不太好算，考慮算出 \(0,2\) 個(gè)連通塊的答案后用 \((n-1)!\) 減掉。
• \(2\) 個(gè)連通塊：設(shè)與 \(i\) 匹配的這一對(duì)數(shù)的下標(biāo)為 \((x,y)\ (x<i<y)\)，那么 \([l,r]\) 這個(gè)區(qū)間相當(dāng)于是除掉 \(x,y,i\) 的部分需要用 \(>a_i\) 的填滿，\(x,y\) 需要用 \(<a_i\) 的填滿，再乘上區(qū)間外的排列數(shù)。方案數(shù)即為 \(\binom{n-i}{y-x-2}\binom{i-1}2(y-x-2)!2!(n-y+x-1)!\)。

直接枚舉 \(i,x,y\) 是 \(O(n^3)\) 的。注意到對(duì)于 \(x,y\) 我們只關(guān)心 \(y-x\)，所以考慮枚舉 \(y-x\in(k,n)\) 并計(jì)算一對(duì) \((i,y-x)\) 對(duì)答案的貢獻(xiàn)個(gè)數(shù)即可。每種方案都會(huì)貢獻(xiàn)一個(gè) \(a_i\)時(shí)間復(fù)雜度 \(O(n^2)\)。

(D)

問(wèn)題等價(jià)于交換盡可能少的數(shù)，使得所有數(shù)都在 \(1\) 所在的置換環(huán)內(nèi)。要最小化操作，意味著一次交換需要合并兩個(gè)置換環(huán)。

考慮維護(hù) \(1\) 所在置換環(huán)的集合，然后枚舉最小的不在這個(gè)集合內(nèi)的數(shù) \(x\)，現(xiàn)在需要將 \(x\) 和集合內(nèi)的一個(gè)數(shù)交換，并且要盡可能最小化字典序。那么我們交換的數(shù) \(y\) 肯定要盡可能滿足 \(x<y\)，并且 \(y\) 要在序列中排得盡可能前。用線段樹(shù)維護(hù)集合內(nèi)每個(gè)數(shù)在序列中所在的位置即可。如果不存在這個(gè) \(y\)，那就與集合內(nèi)下標(biāo)最大的數(shù)交換即可。時(shí)間復(fù)雜度 \(O(n\log n)\)。

(E)

又詭異又魔怔的構(gòu)造題。

首先觀察樣例給的 \(S=4\) 的構(gòu)造：

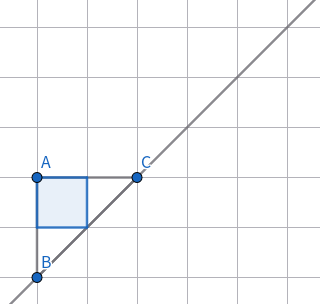
為了方便，我們欽定三個(gè)點(diǎn)的坐標(biāo)為 \(B(0,0),A(0,2),C(2,2)\)。

如果我們沿著斜線 \(y=x\) 向上，那么這時(shí)仍然只有一個(gè)正方形：

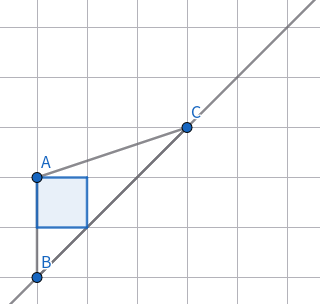
上圖的三角形面積為 \(3\)，即 \(S=6\)。

以此類推，每次我們沿著斜線 \(y=x\) 向上一格，增加的面積都是形如下圖的紅色三角形：

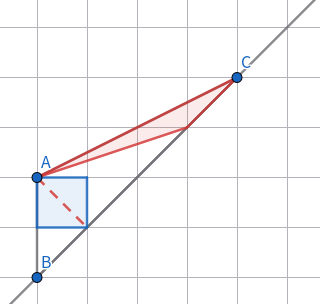
它的底、高均為 \(\sqrt2\)，所以增加的面積即為 \(2\)。

于是 \(2\mid S\) 時(shí)有可以構(gòu)造 \(B(0,0),A(0,2),C\left(\dfrac S2,\dfrac S2\right)\)，而 \(S=2\) 時(shí)似乎是無(wú)解的。

那 \(2\nmid S\) 時(shí)怎么辦呢？

嘗試手畫(huà)一下，似乎 \(S\le 7\) 都沒(méi)有解。這個(gè)包括前面這個(gè) \(S=2\)，其實(shí)我都不太會(huì)嚴(yán)謹(jǐn)?shù)刈C明，希望有大手子教教如何嚴(yán)謹(jǐn)證明。

但總之我們可以得到如下一種 \(S=9\) 的構(gòu)造：

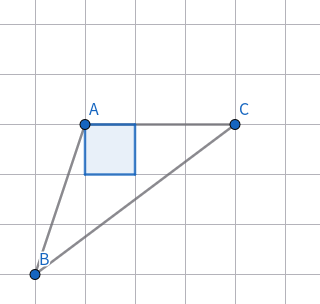
類比 \(2\mid S\) 的情況，我們嘗試將點(diǎn) \(C\) 放在 \(y=x\) 上：

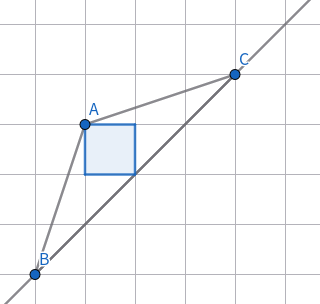
這時(shí)若 \(C\) 的坐標(biāo)為 \((x,x)\)，則 \(S_{\triangle ABC}=\dfrac 12\cdot\sqrt2\cdot\sqrt2x=x\)，故 \(C\left(\dfrac S2,\dfrac S2\right)\)。事實(shí)上你也可以根據(jù) \(2\mid S\) 時(shí)的構(gòu)造將點(diǎn) \(A\) 沿著平行于 \(y=x\) 的直線移動(dòng)得到這種構(gòu)造。

觀察到 \(S=9\) 的時(shí)候，點(diǎn) \(C\) 向右移動(dòng)了一個(gè)單位。我們類似地移動(dòng)一下：

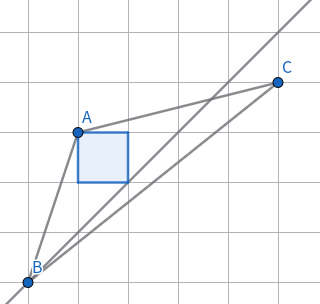
顯然（顯然嗎？）由于這個(gè)移動(dòng)無(wú)法使得任意一個(gè)正方形在三角形內(nèi)的格點(diǎn)數(shù)從 \(3\) 變成 \(4\)，所以這樣一個(gè)移動(dòng)，三角形內(nèi)部沒(méi)有辦法產(chǎn)生一個(gè)新的正方形。這時(shí)設(shè) \(C\left(x,x-1\right)\)，則可以大力割補(bǔ)法求得 \(S_{\triangle ABC}=\dfrac{(x-1)x}2-\dfrac32-\dfrac{(x-1)(x-4)}2-(x-4)=x+\dfrac12\)。故 \(C\left(\dfrac{S-1}2,\dfrac{S-3}2\right)\)。

**F [未做]

不會(huì)多項(xiàng)式。

ARC168

(A)

顯然一段極長(zhǎng)的 \(\tt>>\cdots>\)，假設(shè)長(zhǎng)度為 \(k\)，必然會(huì)對(duì)答案造成 \(\binom{k+1}2\) 的貢獻(xiàn)。同時(shí)，只要我們讓每一段 \(\tt >\) 或 \(\tt <\) 之間段內(nèi)最小值比前一段的最大值大，那么就不會(huì)額外造成貢獻(xiàn)了。

[B]

首先顯然地，根據(jù) Nim 博弈的結(jié)論，若 \(\bigoplus a_i>0\)，那么先手必勝，于是這個(gè)上界 \(k\) 就沒(méi)有必要，也就不存在最大值。

否則按照原本的 Nim 博弈的規(guī)則必?cái)。谑俏覀冃枰粋€(gè)限制 \(k\) 來(lái)想辦法讓先手必勝。

首先假設(shè)存在兩堆石子的個(gè)數(shù)相同，那么這時(shí)可以模仿另一人的行動(dòng)來(lái)消去這兩堆。這樣剩下的石子堆個(gè)數(shù)互不相同。若被消完了那還是先手必?cái)　?/p>

設(shè)剩下的石子堆中最大的為 \(x\)，若設(shè) \(k=x-1\)，那么 \(x\) 必然可以被先手控制在兩步消掉，而 \(<x\) 的石子堆依然可以看作是正常的 Nim 博弈。而這些剩下的石子個(gè)數(shù)異或和就 \(>0\) 了，所以先手必勝。

C

考慮交換字符的情況，即為 \(\tt AB,\tt BC,\tt AC\) 交換，以及 \(\tt BCA\) 和 \(\tt CAB\) 兩種輪換。分別枚舉前三種的交換對(duì)數(shù)，以及輪換的對(duì)數(shù)，分別對(duì)于每種輪換算出實(shí)際上的 \(\tt AB,BC,AC\) 交換對(duì)數(shù)，然后使用多重組合數(shù)計(jì)算即可。時(shí)間復(fù)雜度 \(O(n+k^4)\)。

D

感覺(jué)以前模擬賽做到過(guò)啊。但是我怎么大大地降智。

考慮對(duì)著被染色的序列做區(qū)間 dp。設(shè) \(f_{l,r}\) 為給 \([l,r]\) 內(nèi)的格子染色最多可以改變的狀態(tài)數(shù)。考慮最后一次改變狀態(tài)時(shí)被覆蓋的白色格子 \(k\in[l,r]\)，我們需要一個(gè) \(g_{l,r,k}\) 表示格子 \(k\) 能否被一個(gè)區(qū)間 \([x,y]\in[l,r]\) 所染色。\(g\) 可以在讀入?yún)^(qū)間 \([l,r]\) 的時(shí)候賦 \(i\in[l,r],g_{l,r,i}=\tt True\)，然后按照區(qū)間長(zhǎng)度向外拓展更新，即 \(g_{l,r,i}=g_{l,r,i}\lor g_{l+1,r,i}\lor g_{l,r-1,i}\)。

求得 \(g\) 后，\(f\) 就有狀態(tài)轉(zhuǎn)移式：

時(shí)間復(fù)雜度 \(O(n^3)\)。

*E

生氣了，本來(lái)想對(duì)著恰好 \(k\) 個(gè)做 wqs 二分結(jié)果發(fā)現(xiàn)這東西根本不是凸的！！

假設(shè)序列的某一種劃分得到了代價(jià) \(w\)，則一定可以得到代價(jià)為 \(w-1\) 的劃分方案，也就是答案是單調(diào)的。考慮二分答案 \(w\)，判斷劃分的段中有 \(w\) 個(gè)滿足和 \(\ge s\) 時(shí)，能否劃分出 \(\ge k\) 個(gè)段。

然后要開(kāi)始刻畫(huà)這個(gè)判定了，這個(gè)刻畫(huà)真的難吧！！！

現(xiàn)在相當(dāng)于，要選出 \(w\) 個(gè)段內(nèi)總和 \(\ge s\) 的區(qū)間 \([l_i,r_i]\)，然后貪心地，我們將未選的部分都變成單個(gè)數(shù)構(gòu)成的區(qū)間。發(fā)現(xiàn)我們劃分出的總區(qū)間數(shù)，可以刻畫(huà)成 \(n-\sum\limits_{i=1}^w(r_i-l_i)\)。令 \(h(x)=\min\left\{\sum\limits_{i=1}^x(r_i-l_i)\right\}\)，那二分的判定就有 \(n-h(w)\ge k\)，即 \(h(w)\le n-k\)。

現(xiàn)在要單點(diǎn)求 \(h(w)\)。容易感受出來(lái) \(h(x)\) 是上凸的，所以這個(gè)時(shí)候就可以 wqs 二分了。二分一個(gè)斜率 \(k_0\)，要最大化 \(b_0=h(x)-k_0x\)。那么每選出一個(gè)區(qū)間就會(huì)有一個(gè) \(-k_0\) 的額外貢獻(xiàn)。

于是內(nèi)部可以容易地 dp，設(shè) \(f_i\) 表示掃到位置 \(i\) 時(shí)和 \(\ge s\) 的段的最小代價(jià)，\(g_i\) 為對(duì)應(yīng)的區(qū)間個(gè)數(shù)。仍舊貪心地，設(shè) \(p_i=\max\left\{x\left|\sum\limits_{j=x}^ia_i\ge s\right.\right\}\)，則容易得到轉(zhuǎn)移式：

\(g_i\) 從 \(f_i\) 對(duì)應(yīng)的轉(zhuǎn)移位置轉(zhuǎn)移過(guò)來(lái)即可。時(shí)間復(fù)雜度 \(O(n\log n\log V)\)。

**F

這個(gè)好像前幾周才被搬到聯(lián)考啊！

考慮到整個(gè)操作的過(guò)程中，\(a_i\) 始終單調(diào)不降。考慮維護(hù)差分?jǐn)?shù)組 \(d_i=a_i-a_{i-1}\)。那么最終所有數(shù)的和為 \(\sum\limits_{i=1}^m(m-i+1)d_i\)。

想一下怎么刻畫(huà)操作。考慮維護(hù)一個(gè)堆，每次向堆中加入 \(d_i\) 個(gè) \(m-i+1\)。操作完后將堆中的數(shù)求和。

這個(gè)將部分?jǐn)?shù) \(-1\) 操作似乎并不能很好地表現(xiàn)出來(lái)，考慮轉(zhuǎn)化一下操作。

做第 \(i\) 次操作等價(jià)于先將 \(j\in(x_i,m]\) 的位置 \(+2\)，然后再對(duì)全體 \(-1\)，并對(duì) \(0\) 取 \(\max\)。

• 對(duì)于后綴 \(+2\) 操作，相當(dāng)于是執(zhí)行 \(d_{x_i+1}\gets d_{x_i+1}+2\)。也就是向堆中加入 \(2\) 個(gè) \(m-x_i\)。
• 對(duì)于全體 \(-1\) 并對(duì) \(0\) 取 \(\max\) 的操作，相當(dāng)于是從左到右，找到一個(gè)非零的 \(d_i\)，執(zhí)行 \(d_i\gets d_i-1\)。這個(gè)相當(dāng)于在堆中刪除了一個(gè) \(m-i\)，由于 \(i\) 要盡可能小，所以就等價(jià)于從堆中刪去 \(1\) 個(gè)最大的數(shù)。

所以現(xiàn)在的問(wèn)題就相當(dāng)于要維護(hù)一個(gè)大根堆，最終要求堆內(nèi)數(shù)的和。而 \(x_i\) 會(huì)修改，這個(gè)「最大數(shù)」并不好求。

考慮將問(wèn)題弱化一下。我們將「刪除最大數(shù)，求最終的和」轉(zhuǎn)化成「刪除任意數(shù)，最小化最終的和」。這顯然是等價(jià)的。這樣一個(gè)最小化問(wèn)題，可以考慮構(gòu)建費(fèi)用流模型：

• \(S\overset{(2,m-x_i)}{\longrightarrow}i\)，這個(gè)刻畫(huà)了「加入 \(2\) 個(gè) \(m-x_i\)」。
• \(i\overset{(+\infin,0)}{\longrightarrow}j\ (i<j)\)，這個(gè)刻畫(huà)了「在第 \(i\) 次操作中加入的數(shù)在第 \(j\) 次操作時(shí)被刪除」。
• \(i\overset{(1,0)}{\longrightarrow}T\)，這個(gè)刻畫(huà)了「在第 \(i\) 次操作時(shí)刪除 \(1\) 個(gè)數(shù)」。

對(duì)于第二種連邊顯然可以變?yōu)?\(i\overset{(+\infin,0)}{\longrightarrow}i+1\)。

于是答案即為最小費(fèi)用最大流。接下來(lái)當(dāng)然考慮模擬費(fèi)用流。

我們會(huì)先找到一個(gè)最大流，然后找一個(gè)環(huán)去增廣。可以增廣的環(huán)必然是包含 \(S\) 的（因?yàn)榘?\(T\) 的環(huán)沒(méi)有費(fèi)用，不造成任何影響）。

一次對(duì) \(x_i\) 的單點(diǎn)修改，當(dāng)然只會(huì)增廣一個(gè)包含 \(i\) 的環(huán) \(S\to u\rightsquigarrow v\to S\)。\(i\) 一定是 \(u,v\) 之一，不然這個(gè)環(huán)在修改前增廣一定不劣。

討論 \(x_i\) 是改大了還是改小了，以此來(lái)討論增廣的是順向的 \(S\to i\rightsquigarrow j\to S\) 還是逆向的 \(S\to j\rightsquigarrow i\to S\)。用線段樹(shù)維護(hù)可以點(diǎn) \(i\) 向前和向后可以達(dá)到的點(diǎn)，維護(hù)區(qū)間最值后線段樹(shù)二分即可。

時(shí)間復(fù)雜度 \(O((n+q)\log n)\)。

ARC169

(A)

建樹(shù)。顯然深度最深的點(diǎn)會(huì)對(duì)答案產(chǎn)生更大的影響。由于這些點(diǎn)的權(quán)值最終都會(huì)傳到根節(jié)點(diǎn)，所以可以求和看正負(fù)性。如果恰為 \(0\) 再看深度第二深的節(jié)點(diǎn)，以此類推。

(B)

考慮 dp。設(shè) \(f_i\) 表示以 \(i\) 結(jié)尾的區(qū)間的總貢獻(xiàn)。設(shè) \(p_i=\min\left\{x\left|\sum\limits_{j=x}^ia_i\le s\right.\right\}\)，則區(qū)間 \([i,i],[i-1,i],\cdots,[p_i,i]\) 的答案都為 \(1\)，而左端點(diǎn) \(<p_i\) 的需要進(jìn)一步拆，而這個(gè)可以從 \(f_{p_i-1}\) 轉(zhuǎn)移過(guò)來(lái)，即有：

答案即為 \(\sum\limits_{i=1}^nf_i\)。\(p_i\) 可以雙指針求得，時(shí)間復(fù)雜度 \(O(n)\)。

(C)

題目的限制是基于一個(gè)相同數(shù)的連續(xù)段的長(zhǎng)度，于是考慮對(duì)著連續(xù)段 dp。設(shè) \(f_{i,j}\)，表示考慮了前 \(i\) 個(gè)數(shù)，其中第 \(i\) 個(gè)數(shù)為 \(j\)，并欽定 \(j\) 是其所在連續(xù)段的最后一個(gè)數(shù)。那么容易的得到轉(zhuǎn)移式：

這個(gè)給 \(f\) 和 \(f_{*,x}\) 各求一個(gè)前綴和就可以優(yōu)化轉(zhuǎn)移。時(shí)間復(fù)雜度 \(O(n^2)\)。

D

設(shè) \(a_i\) 最終變化為 \(b_i\)。放在 \(\bmod\ n\) 的意義下挺難思考的。考慮忽略這個(gè) \(\bmod\ n\)。容易發(fā)現(xiàn)，如果將 \(a_i\) 升序排列，那么讓 \(b_i\) 升序是一定不劣的。

考慮 \(b_i\) 會(huì)滿足的約束：

• \(a_i\le b_i\)。因?yàn)?\(a_i\) 只會(huì)增加不會(huì)減少。
• \(b_i\) 為 \(\bmod\ n\) 的完全剩余系。因?yàn)槲覀円婚_(kāi)始忽略了取模，但是取模后仍然需要滿足題目條件。
• \(m\left|\sum\limits_{i=1}^n(b_i-a_i)\right.\)。每次都是恰好對(duì) \(m\) 個(gè)數(shù) \(+1\)，總變化量當(dāng)然得是 \(m\) 的倍數(shù)。
• \(\max\limits_{i=1}^n\{b_i-a_i\}\le\dfrac{\sum\limits_{i=1}^n(b_i-a_i)}m\)。一個(gè)數(shù)被增加的次數(shù)顯然不會(huì)超過(guò)增加總數(shù)的平均數(shù)。

不難發(fā)現(xiàn)以上的條件結(jié)合起來(lái)是充要的。

首先，如果有 \(b_1+n<b_n\)，那么將 \(b_1\) 變成 \(b_n-n\)，將 \(b_n\) 變成 \(b_1+n\)，這時(shí)的 \(b_i\) 依舊是 \(\bmod\ n\) 的完全剩余系。因此我們必然存在一個(gè)最優(yōu)方案滿足 \(b_i=b_{i-1}+1\)。

然后暴力枚舉，找到 \(b_1\) 最小的滿足前三個(gè)條件的 \(b\)。

最后需要滿足第四個(gè)條件，令當(dāng)前 \(b_i\) 的和為 \(s\)，那么根據(jù)以上約束，答案一定形如一個(gè) \(s+k\cdot\text{lcm}(n,m)\)，其中 \(k\) 非負(fù)。

注意到對(duì)于第三個(gè)條件，隨著 \(b_1\) 上升，小于等于號(hào)左邊的式子增長(zhǎng)不會(huì)比右邊快。所以二分即可。時(shí)間復(fù)雜度 \(O(n+\log V)\)。

*E

顯然 \(B\) 個(gè)數(shù)比 \(R\) 少必然無(wú)解。