前言

排序算法是老生常談的了，但是在面試中也有會(huì)被問到，例如有時(shí)候，在考察算法能力的時(shí)候，不讓你寫算法，就讓你描述一下，某個(gè)排序算法的思想以及時(shí)間復(fù)雜度或空間復(fù)雜度。我就遇到過，直接問快排的，所以這次我就總結(jié)梳理一下經(jīng)典的十大排序算法以及它們的模板代碼。

算法分析

一個(gè)排序算法的好壞，一般是通過下面幾個(gè)關(guān)鍵信息來分析的，下面先介紹一下這幾個(gè)關(guān)鍵信息，然后再將常見的排序算法的這些關(guān)鍵信息統(tǒng)計(jì)出來。

名詞介紹

• 時(shí)間復(fù)雜度：指對(duì)數(shù)據(jù)操作的次數(shù)（或是簡(jiǎn)單的理解為某段代碼的執(zhí)行次數(shù)）。舉例：O(1)：常數(shù)時(shí)間復(fù)雜度；O(log n)：對(duì)數(shù)時(shí)間復(fù)雜度；O(n)：線性時(shí)間復(fù)雜度。
• 空間復(fù)雜度：某段代碼每次執(zhí)行時(shí)需要開辟的內(nèi)存大小。
• 內(nèi)部排序：不依賴外部的空間，直接在數(shù)據(jù)內(nèi)部進(jìn)行排序；
• 外部排序：數(shù)據(jù)的排序，不能通過內(nèi)部空間來完成，需要依賴外部空間。
• 穩(wěn)定排序：若兩個(gè)元素相等：a=b，排序前a排在b前面，排序后a仍然在b后面，稱為穩(wěn)定排序。
• 不穩(wěn)定排序：若兩個(gè)元素相等：a=b，排序前a排在b前面，排序后a有可能出現(xiàn)在b后面，稱為不穩(wěn)定排序。

常見的排序算法的這幾個(gè)關(guān)鍵信息如下：

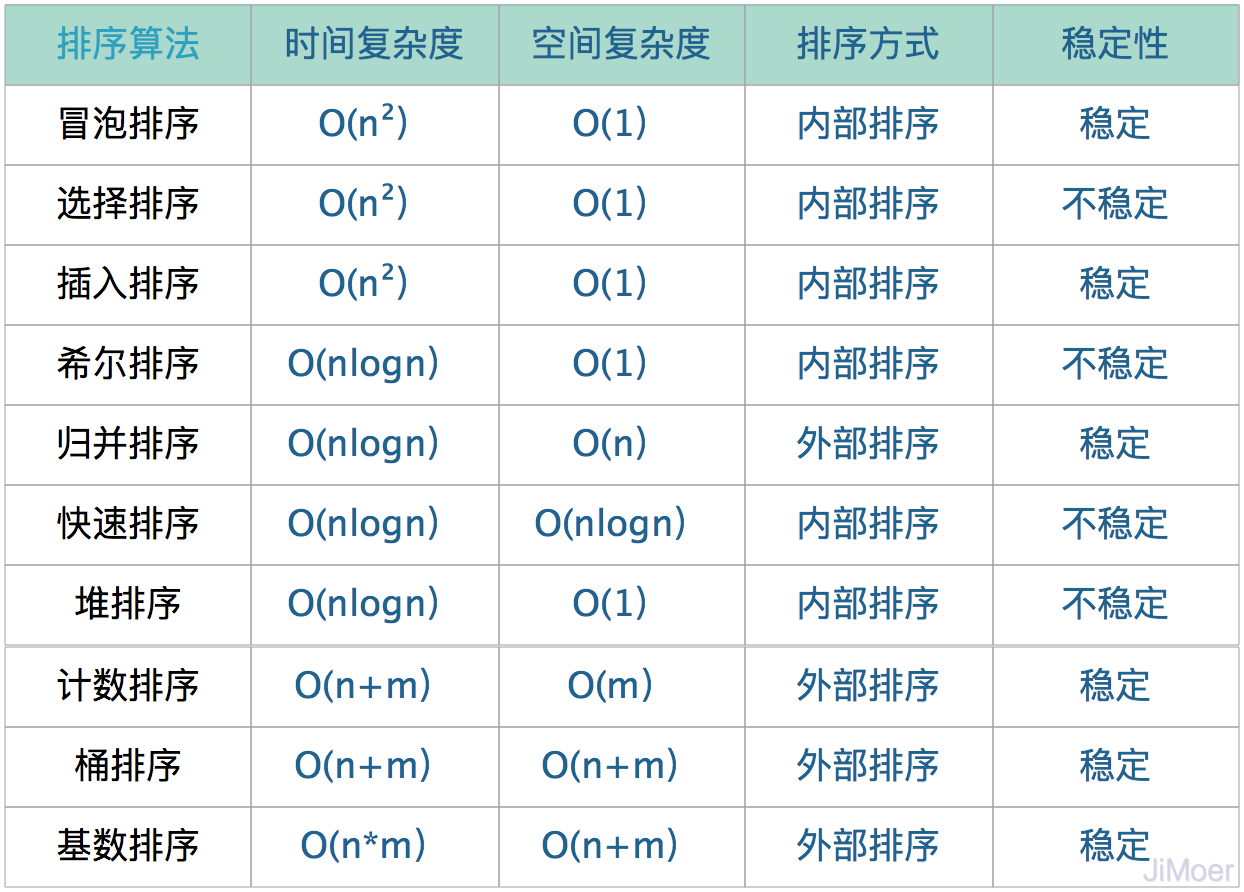
冒泡排序

冒泡排序是一種簡(jiǎn)單直觀的排序算法，它需要多次遍歷數(shù)據(jù)；
主要有這么幾步：

• 將相鄰的兩個(gè)元素進(jìn)行比較，如果前一個(gè)元素比后一個(gè)元素大那么就交換兩個(gè)元素的位置，經(jīng)過這樣一次遍歷后，最后一個(gè)元素就是最大的元素了；
• 然后再將除最后一個(gè)元素的剩下的元素，重復(fù)執(zhí)行上面相鄰兩元素比較的步驟。
• 每次對(duì)越來越少的元素重復(fù)上面的步驟，直到就剩一個(gè)數(shù)字需要比較。

這樣最終達(dá)到整體數(shù)據(jù)的一個(gè)有序性了。

動(dòng)圖演示

代碼模板

/**
 * 冒泡排序
 * @param array
 */
public static void bubbleSort(int[] array){
    if(array.length == 0){
        return;
    }
    for(int i=0;i<array.length;i++){
        // 每一次都減少i個(gè)元素
        for(int j=0;j<array.length-1-i;j++){
            // 若相鄰的兩個(gè)元素比較后，前一個(gè)元素大于后一個(gè)元素，則交換位置。
            if(array[j]>array[j+1]){
                int temp = array[j];
                array[j] = array[j+1];
                array[j+1] = temp;
            }
        }
    }
}

冒泡排序總結(jié)

當(dāng)數(shù)組中的元素已經(jīng)是正序時(shí)，執(zhí)行效率最高。
當(dāng)數(shù)組中的元素是一個(gè)倒序時(shí)，執(zhí)行效率最低，相鄰的元素每次比較都需要交換位置。
而且冒泡排序是完全在數(shù)據(jù)內(nèi)部進(jìn)行的，不需要額外的空間，所以空間復(fù)雜度是O(1)。

選擇排序

選擇排序是一種簡(jiǎn)單粗暴的排序方式，每次都從數(shù)據(jù)中選出最大或最小的元素，最終選完了，那么選出來的數(shù)據(jù)就是排好序的了。

主要步驟：

• 先從全部數(shù)據(jù)中選出最小的元素，放到第一個(gè)元素的位置（選出最小元素和第一位位置交換位置）；
• 然后再?gòu)某说谝粋€(gè)元素的剩余元素中再選出最小的元素，然后放到數(shù)組的第二個(gè)位置上。
• 循環(huán)重復(fù)上面的步驟，最終選出來的數(shù)據(jù)都放前面了，數(shù)據(jù)就排好序了。

動(dòng)圖演示

代碼模板

public static void selectSort(int[] array){

    for(int i=0;i<array.length;i++){
        // 先以i為最小值的下標(biāo)
        int min = i;
        // 然后從后面的數(shù)據(jù)中找出比array[min] 還小的值，就替換min為當(dāng)前下標(biāo)。
        for(int j=i+1;j<array.length;j++){
            if(array[j]<array[min]){
                min = j;
            }
        }
        // 最終如果最小值的下標(biāo)不等于i了，那么將最小值與i位置的數(shù)據(jù)替換，即將最小值放到數(shù)組前面來，然后循環(huán)整個(gè)操作。
        if(min != i){
            int temp = array[i];
            array[i] = array[min];
            array[min] = temp;
        }
    }
}

選擇排序總結(jié)

所有的數(shù)據(jù)經(jīng)過選擇排序，時(shí)間復(fù)雜度都是O(n^2)；所以需要排序的數(shù)據(jù)量越小選擇排序的效率越高。

插入排序

插入排序也是一種比較直觀和容易理解的排序算法，通過構(gòu)建有序序列，將未排序中的數(shù)據(jù)插入到已排序中序列，最終未排序全部插入到有序序列，達(dá)到排序效果。

主要步驟：

• 將原始數(shù)據(jù)的第一個(gè)元素當(dāng)成已排序序列，然后將除了第一個(gè)元素的后面元素當(dāng)成未排序序列。
• 從后面未排序元素中從前到后掃描，挨個(gè)取出元素，在已排序的序列中從后往前掃描，將從未排序序列中取出的元素插入到已排序序列的指定位置。
• 當(dāng)未排序元素?cái)?shù)量為0時(shí)，則排序完成。

動(dòng)圖演示

代碼模板

public static void insertSort(int[] array){
     // 第一個(gè)元素被認(rèn)為默認(rèn)有序，所以遍歷無(wú)序元素從i1開始。
     for(int i=1;i<array.length;i++){

         int sortItem = array[i];
         int j = i;
         // 將當(dāng)前元素插入到前面的有序元素里，將當(dāng)前元素與前面有序元素從后往前挨個(gè)對(duì)比，然后將元素插入到指定位置。
         while (j>0 && sortItem < array[j-1]){
             array[j] = array[j-1];
             j--;
         }
         // 若當(dāng)前元素在前面已排序里面不是最大的，則將它插入到前面已經(jīng)確定了位置里。
         if(j !=i){
             array[j] = sortItem;
         }
     }
 }

插入排序總結(jié)

插入排序也是采用的內(nèi)部排序，所以空間復(fù)雜度是O(1)，但是時(shí)間復(fù)雜度就是O(n^2)，因?yàn)榛旧厦總€(gè)元素都要處理多次，需要反復(fù)將已排序元素移動(dòng)，然后將數(shù)據(jù)插入到指定的位置。

希爾排序

希爾排序是插入排序的一個(gè)升級(jí)版，它主要是將原先的數(shù)據(jù)分成若干個(gè)子序列，然后將每個(gè)子序列進(jìn)行插入排序，然后每次拆得子序列數(shù)量逐次遞減，直到拆的子序列的長(zhǎng)度等于原數(shù)據(jù)長(zhǎng)度。然后再將數(shù)據(jù)整體來依次插入排序。

主要步驟：
選擇一個(gè)增量序列 t1，t2，……，tk，其中 ti > tj, tk = 1；
按增量序列個(gè)數(shù) k，對(duì)序列進(jìn)行 k 趟排序；
每趟排序，根據(jù)對(duì)應(yīng)的增量 ti，將待排序列分割成若干長(zhǎng)度為 m 的子序列，分別對(duì)各子表進(jìn)行直接插入排序。僅增量因子為 1 時(shí)，整個(gè)序列作為一個(gè)表來處理，表長(zhǎng)度即為整個(gè)序列的長(zhǎng)度。

過程演示

原始未排序的數(shù)據(jù)。

經(jīng)過初始增量gap=array.length/2=5分組后，將原數(shù)據(jù)分為了5組，[12,1]、[29,30]、[5,45]、[16,26]、[15,32]。

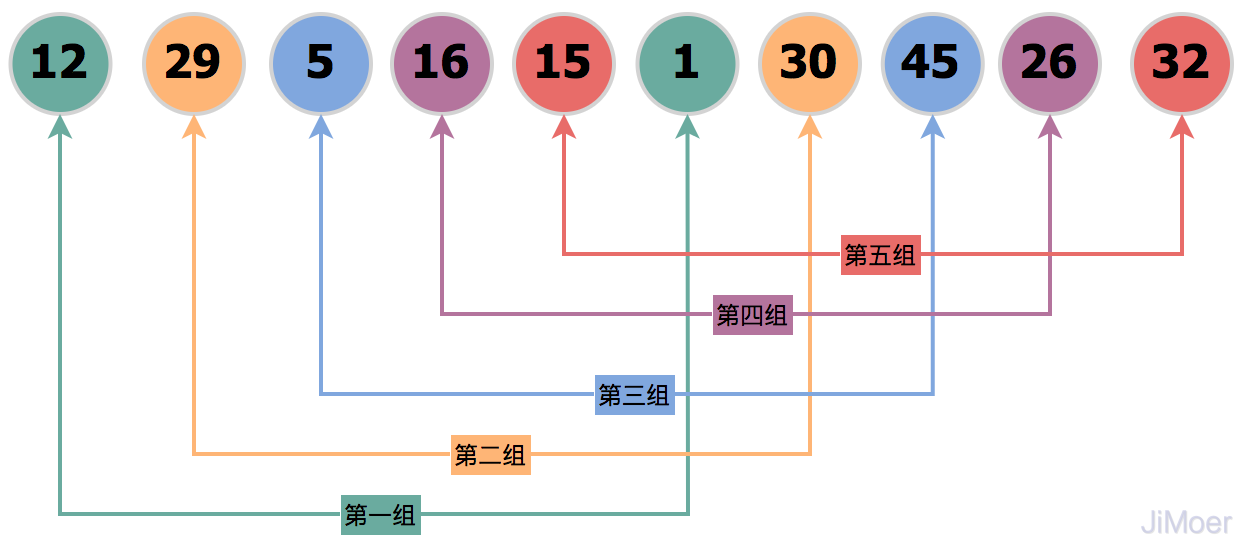
將分組后的數(shù)據(jù)，每一組數(shù)據(jù)都直接執(zhí)行插入排序，這樣數(shù)據(jù)已經(jīng)慢慢有序起來了，然后再縮小增量gap=5/2=2，將數(shù)據(jù)分為2組：[1,5,15,30,26]、[29,16,12,45,32]。

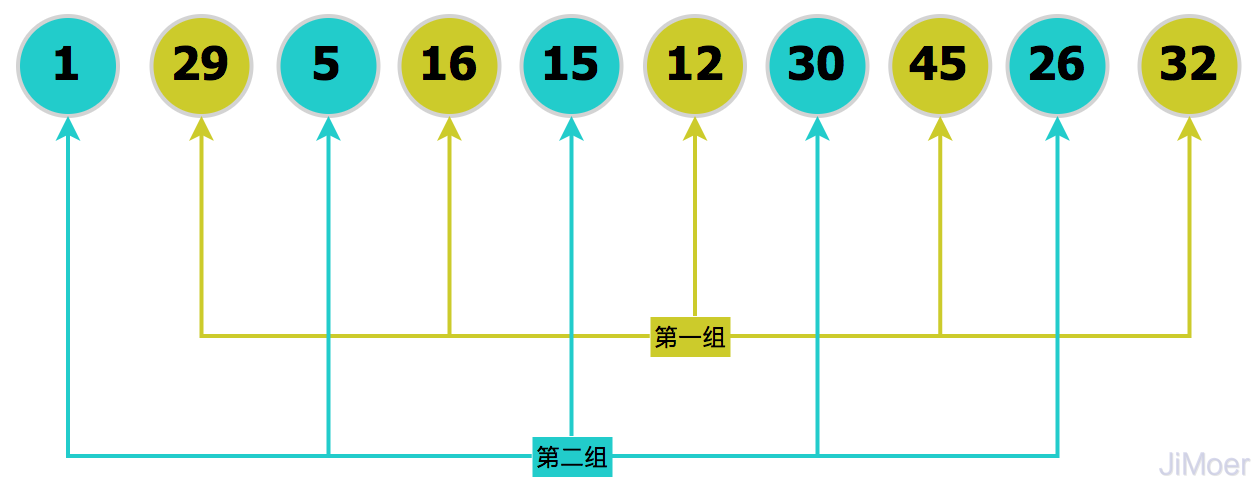
對(duì)上面已經(jīng)分好的兩組進(jìn)行插入排序，整個(gè)數(shù)據(jù)就更加趨向有序了，然后再縮小增量gap=2/2=1，整個(gè)數(shù)據(jù)成為了1組，整個(gè)序列作為了表來處理，然后再執(zhí)行一次插入排序，數(shù)據(jù)最終達(dá)到了有序。

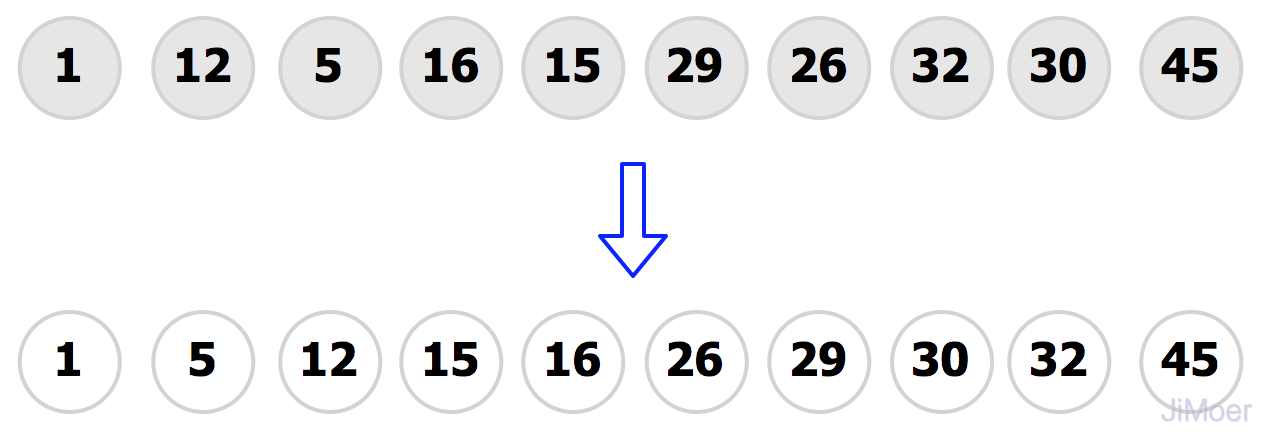
代碼模板

/**
 * 希爾排序
 * @param array
 */
public static void shellSort(int[] array){
    int len = array.length;
    int temp, gap = len / 2;
    while (gap > 0) {
        for (int i = gap; i < len; i++) {
            temp = array[i];
            int preIndex = i - gap;
            while (preIndex >= 0 && array[preIndex] > temp) {
                array[preIndex + gap] = array[preIndex];
                preIndex -= gap;
            }
            array[preIndex + gap] = temp;
        }
        gap /= 2;
    }
}

歸并排序

歸并排序是采用的分而治之的遞歸方式來完成數(shù)據(jù)排序的，主要是將已有序的兩個(gè)子序列，合并成一個(gè)新的有序子序列。先將子序列分段有序，然后再將分段后的子序列合并成，最終完成數(shù)據(jù)的排序。

主要步驟：

• 將數(shù)據(jù)的長(zhǎng)度從中間一分為二，分成兩個(gè)子序列，執(zhí)行遞歸操作，直到每個(gè)子序列就剩兩個(gè)元素。
• 然后分別對(duì)這些拆好的子序列進(jìn)行歸并排序。
• 將排序好的子序列再兩兩合并，最終合并成一個(gè)完整的排序序列。

動(dòng)圖演示

代碼模板

/**
     * 歸并排序
     * @param array     數(shù)組
     * @param left      0
     * @param right     array.length-1
     */
    public static void mergeSort(int[] array,int left,int right){
        
        if (right <= left){
            return;
        }
        // 一分為二
        int mid = (left + right)/2;
        // 對(duì)前半部分執(zhí)行歸并排序
        mergeSort(array, left, mid);
        // 對(duì)后半部分執(zhí)行歸并排序
        mergeSort(array, mid + 1, right);
        // 將分好的每個(gè)子序列，執(zhí)行排序加合并操作
        merge(array, left, mid, right);
    }

    /**
     * 合并加排序
     * @param array
     * @param left
     * @param middle
     * @param right
     */
    public static void merge(int[] array,int left,int middle,int right){
     // 中間數(shù)組
     int[] temp = new int[right - left + 1]; 
     int i = left, j = middle + 1, k = 0;
     while (i <= middle && j <= right) {
         // 若前面數(shù)組的元素小，就將前面元素的數(shù)據(jù)放到中間數(shù)組中
         if(array[i] <= array[j]){
             temp[k++] = array[i++];
         }else {
             // 若后面數(shù)組的元素小，就將后面數(shù)組的元素放到中間數(shù)組中
             temp[k++] = array[j++];
         }
     }
     // 若經(jīng)過上面的比較合并后，前半部分的數(shù)組還有數(shù)據(jù)，則直接插入中間數(shù)組后面
     while (i <= middle){
         temp[k++] = array[i++];
     }
     // 若經(jīng)過上面的比較合并后，后半部分的數(shù)組還有數(shù)據(jù)，則直接插入中間數(shù)組后面
     while (j <= right){
         temp[k++] = array[j++];
     }
     // 將數(shù)據(jù)從中間數(shù)組中復(fù)制回原數(shù)組
     for (int p = 0; p < temp.length; p++) {
         array[left + p] = temp[p];
     }
 }

歸并排序總結(jié)

歸并排序效率很高，時(shí)間復(fù)雜度能達(dá)到O(nlogn)，但是依賴額外的內(nèi)存空間，而且這種分而治之的思想很值得借鑒，很多場(chǎng)景都是通過簡(jiǎn)單的功能，組成了復(fù)雜的邏輯，所以只要找到可拆分的最小單元，就可以進(jìn)行分而治之了。

快速排序

快速排序，和二分查找的思想很像，都是先將數(shù)據(jù)一份為二然后再逐個(gè)處理。快速排序也是最常見的排序算法的一種，面試被問到的概率還是比較大的。

主要步驟：

• 從數(shù)據(jù)中挑選出一個(gè)元素，稱為 "基準(zhǔn)"（pivot），一般選第一個(gè)元素或最后一個(gè)元素。
• 然后將數(shù)據(jù)中，所有比基準(zhǔn)元素小的都放到基準(zhǔn)元素左邊，所有比基準(zhǔn)元素大的都放到基準(zhǔn)元素右邊。
• 然后再將基準(zhǔn)元素前面的數(shù)據(jù)集合和后面的數(shù)據(jù)集合重復(fù)執(zhí)行前面兩步驟。

動(dòng)圖演示

代碼模板

/**
 * 快速排序
 * @param array 數(shù)組
 * @param begin 0
 * @param end   array.length-1
 */
public static void quickSort(int[] array, int begin, int end) {
    if (end <= begin) return;
    int pivot = partition(array, begin, end);
    quickSort(array, begin, pivot - 1);
    quickSort(array, pivot + 1, end);
}

/**
 * 分區(qū)
 * @param array
 * @param begin
 * @param end
 * @return
 */
public static int partition(int[] array, int begin, int end) {
    // pivot: 標(biāo)桿位置，counter: 小于pivot的元素的個(gè)數(shù)
    int pivot = end, counter = begin;
    for (int i = begin; i < end; i++) {
        if (array[i] < array[pivot]) {
           // 替換，將小于標(biāo)桿位置的數(shù)據(jù)放到開始位置算起小于標(biāo)桿數(shù)據(jù)的第counter位
            int temp = array[counter];
            array[counter] = array[i];
            array[i] = temp;
            counter++;
        }
    }
    // 將標(biāo)桿位置的數(shù)據(jù)移動(dòng)到小于標(biāo)桿位置數(shù)據(jù)的下一個(gè)位。
    int temp = array[pivot];
    array[pivot] = array[counter];
    array[counter] = temp;
    return counter;
}

快速排序總結(jié)

我找的快速排序的模板代碼，是比較巧妙的，選擇了最后一個(gè)元素作為了基準(zhǔn)元素，然后小于基準(zhǔn)元素的數(shù)量，就是基準(zhǔn)元素應(yīng)該在的位置。這樣看起來是有點(diǎn)不好懂，但是看明白之后，就會(huì)覺得這個(gè)模板寫的還是比較有意思的。

堆排序

堆排序其實(shí)是采用的堆這種數(shù)據(jù)結(jié)構(gòu)來完成的排序，一般堆排序的方式都是采用的一種近似完全二叉樹來實(shí)現(xiàn)的堆的方式完成排序，但是堆的實(shí)現(xiàn)方式其實(shí)不止有用二叉樹的方式，其實(shí)還有斐波那契堆。
而根據(jù)排序的方向又分為大頂堆和小頂堆：

• 大頂堆：每個(gè)節(jié)點(diǎn)值都大于或等于子節(jié)點(diǎn)的值，在堆排序中用做升序排序。
• 小頂堆：每個(gè)節(jié)點(diǎn)值都小于或等于子節(jié)點(diǎn)的值，在堆排序中用做降序排序。

像Java中的PriorityQueue就是小頂堆。

主要步驟：

1. 創(chuàng)建一個(gè)二叉堆，參數(shù)就是無(wú)序序列[0~n]；
2. 把堆頂元素和堆尾元素互換；
3. 調(diào)整后的堆頂元素，可能不是最大或最小的值，所以還需要調(diào)整此時(shí)堆頂元素的到正確的位置，這個(gè)調(diào)整位置的過程，主要是和二叉樹的子元素的值對(duì)比后找到正確的位置。
4. 重復(fù)步驟2、步驟3，直至整個(gè)序列的元素都在二叉堆的正確位置上了。

動(dòng)圖演示

模板代碼

/**
 * 堆排序
 * @param array
 */
public static int[] heapSort(int[] array){
    int size = array.length;
    // 先將數(shù)據(jù)放入堆中
    for (int i = (int) Math.floor(size / 2); i >= 0; i--) {
        heapTopMove(array, i, size);
    }
    // 堆頂位置調(diào)整
    for(int i = size - 1; i > 0; i--) {
        swapNum(array, 0, i);
        size--;
        heapTopMove(array, 0,size);
    }
    return array;
}

/**
 * 堆頂位置維護(hù)
 * @param array
 * @param i
 * @param size
 */
public static void heapTopMove(int[] array,int i,int size){

    int left = 2 * i + 1;
    int right = 2 * i + 2;
    int largest = i;

    if (left < size && array[left] > array[largest]) {
        largest = left;
    }

    if (right < size && array[right] > array[largest]) {
        largest = right;
    }

    if (largest != i) {
        swapNum(array, i, largest);
        heapTopMove(array, largest, size);
    }
}

/**
 * 比較交換
 * @param array
 * @param left
 * @param right
 */
public static void swapNum(int[] array,int left,int right){
    int temp = array[left];
    array[left] = array[right];
    array[right] = temp;
}

堆排序總結(jié)

堆排序的時(shí)間復(fù)雜度也是O(nlogn),這個(gè)也是有一定的概率在面試中被考察到，其實(shí)如果真實(shí)在面試中遇到后，可以在實(shí)現(xiàn)上不用自己去維護(hù)一個(gè)堆，而是用Java中的PriorityQueue來實(shí)現(xiàn)，可以將無(wú)序數(shù)據(jù)集合放入到PriorityQueue中，然后再依次取出堆頂數(shù)據(jù)，取出堆頂數(shù)據(jù)時(shí)要從堆中移除取出的這個(gè)元素，這樣每次取出的就都是現(xiàn)有數(shù)據(jù)中最小的元素了。

計(jì)數(shù)排序

計(jì)數(shù)排序是一種線性時(shí)間復(fù)雜度的排序算法，它主要的邏輯時(shí)將數(shù)據(jù)轉(zhuǎn)化為鍵存儲(chǔ)在額外的數(shù)組空間里。計(jì)數(shù)排序有一定的局限性，它要求輸入的數(shù)據(jù)，必須是有確定范圍的整數(shù)序列。

主要步驟：

• 找出待排序的數(shù)組中最大和最小的元素；
• 統(tǒng)計(jì)數(shù)組中每個(gè)值為i的元素出現(xiàn)的次數(shù)，存入數(shù)組C的第i項(xiàng)；
• 對(duì)所有的計(jì)數(shù)累加（從C中的第一個(gè)元素開始，每一項(xiàng)和前一項(xiàng)相加）；
• 反向填充目標(biāo)數(shù)組：將每個(gè)元素i放在新數(shù)組的第C(i)項(xiàng)，每放一個(gè)元素就將C(i)減去1。

動(dòng)圖演示

代碼模板

/**
 * 計(jì)數(shù)排序
 * @param array
 */
public static void countSort(int[] array){
    int bucketLen = getMaxValue(array) + 1;
    int[] bucket = new int[bucketLen];
    // 統(tǒng)計(jì)每個(gè)值出現(xiàn)的次數(shù)
    for (int value : array) {
        bucket[value]++;
    }
    // 反向填充數(shù)組
    int sortedIndex = 0;
    for (int j = 0; j < bucketLen; j++) {
        while (bucket[j] > 0) {
            array[sortedIndex++] = j;
            bucket[j]--;
        }
    }
}

/**
 * 獲取最大值
 * @param arr
 * @return
 */
private static int getMaxValue(int[] arr) {
    int maxValue = arr[0];
    for (int value : arr) {
        if (maxValue < value) {
            maxValue = value;
        }
    }
    return maxValue;
}

桶排序

桶排序算是計(jì)數(shù)排序的一個(gè)加強(qiáng)版，它利用特定函數(shù)的映射關(guān)系，將屬于一定范圍內(nèi)的數(shù)據(jù)，放到一個(gè)桶里，然后對(duì)每個(gè)桶中的數(shù)據(jù)進(jìn)行排序，最后再將排序好的數(shù)據(jù)拼接起來。
主要步驟：

• 設(shè)置一個(gè)合適長(zhǎng)度的數(shù)組作為空桶；
• 遍歷數(shù)據(jù)，將數(shù)據(jù)都放到指定的桶中，分布的越均勻越好；
• 對(duì)每個(gè)非空的桶里的數(shù)據(jù)進(jìn)行排序；
• 將每個(gè)桶中排序好的數(shù)據(jù)拼接在一起。

動(dòng)圖演示

代碼模板

 /**
  * 桶排序
  * @param arr
  * @param bucketSize
  * @return
  */
 private static int[] bucketSort(int[] arr, int bucketSize){
     if (arr.length == 0) {
         return arr;
     }
     int minValue = arr[0];
     int maxValue = arr[0];
     // 計(jì)算出最大值和最小值
     for (int value : arr) {
         if (value < minValue) {
             minValue = value;
         } else if (value > maxValue) {
             maxValue = value;
         }
     }
     // 根據(jù)桶的長(zhǎng)度以及數(shù)據(jù)的最大值和最小值，計(jì)算出桶的數(shù)量
     int bucketCount = (int) Math.floor((maxValue - minValue) / bucketSize) + 1;
     int[][] buckets = new int[bucketCount][0];

     // 利用映射函數(shù)將數(shù)據(jù)分配到各個(gè)桶中
     for (int i = 0; i < arr.length; i++) {
         int index = (int) Math.floor((arr[i] - minValue) / bucketSize);
         // 將數(shù)據(jù)填充到指定的桶中
         buckets[index] = appendBucket(buckets[index], arr[i]);
     }
     int arrIndex = 0;
     for (int[] bucket : buckets) {
         if (bucket.length <= 0) {
             continue;
         }
         // 對(duì)每個(gè)桶進(jìn)行排序，這里使用了插入排序
         InsertSort.insertSort(bucket);
         for (int value : bucket) {
             arr[arrIndex++] = value;
         }
     }
     return arr;
 }

 /**
  * 擴(kuò)容，并追加數(shù)據(jù)
  *
  * @param array
  * @param value
  */
 private static int[] appendBucket(int[] array, int value) {
     array = Arrays.copyOf(array, array.length + 1);
     array[array.length - 1] = value;

     return array;
 }

基數(shù)排序

基數(shù)排序是一種非比較型排序，主要邏輯時(shí)將整數(shù)按位拆分成不同的數(shù)字，然后再按照位數(shù)排序，先按低位排序，進(jìn)行收集，再按高位排序，再進(jìn)行收集，直到最高位。
主要步驟：

• 獲取原始數(shù)據(jù)中的最大值以及最高位；
• 在原始數(shù)組中，從最低位開始取每個(gè)位組成基數(shù)數(shù)組；
• 對(duì)基數(shù)數(shù)組進(jìn)行計(jì)數(shù)排序（利用計(jì)數(shù)排序適用于小范圍數(shù)的特點(diǎn)）；

動(dòng)圖演示

代碼模板

/**
 * 基數(shù)排序
 * @param array
 */
public static void radixSort(int[] array){
    // 獲取最高位
    int maxDigit = getMaxDigit(array);
    int mod = 10;
    int dev = 1;

    for (int i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
        // 考慮負(fù)數(shù)的情況，這里擴(kuò)展一倍隊(duì)列數(shù)，其中 [0-9]對(duì)應(yīng)負(fù)數(shù)，[10-19]對(duì)應(yīng)正數(shù) (bucket + 10)
        int[][] counter = new int[mod * 2][0];
        // 計(jì)數(shù)排序
        for (int j = 0; j < array.length; j++) {
            int bucket = ((array[j] % mod) / dev) + mod;
            counter[bucket] = appendBucket(counter[bucket], array[j]);
        }
        // 反向填充數(shù)組
        int pos = 0;
        for (int[] bucket : counter) {
            for (int value : bucket) {
                array[pos++] = value;
            }
        }
    }
}

/**
 * 獲取最高位數(shù)
 */
private static int getMaxDigit(int[] arr) {
    int maxValue = getMaxValue(arr);
    return getNumLength(maxValue);
}

/**
 * 獲取最大值
 * @param arr
 * @return
 */
private static int getMaxValue(int[] arr) {
    int maxValue = arr[0];
    for (int value : arr) {
        if (maxValue < value) {
            maxValue = value;
        }
    }
    return maxValue;
}

/**
 * 獲取整數(shù)的位數(shù)
 * @param num
 * @return
 */
protected static int getNumLength(long num) {
    if (num == 0) {
        return 1;
    }
    int lenght = 0;
    for (long temp = num; temp != 0; temp /= 10) {
        lenght++;
    }
    return lenght;
}

/**
 * 擴(kuò)容，并追加數(shù)據(jù)
 *
 * @param array
 * @param value
 */
private static int[] appendBucket(int[] array, int value) {
    array = Arrays.copyOf(array, array.length + 1);
    array[array.length - 1] = value;
    return array;
}

基數(shù)排序總結(jié)

計(jì)數(shù)排序、桶排序、基數(shù)排序這三種排序算法都利用了桶的概念，但對(duì)桶的使用方法上有明顯差異：

• 基數(shù)排序：根據(jù)鍵值的每位數(shù)字來分配桶；
• 計(jì)數(shù)排序：每個(gè)桶只存儲(chǔ)單一鍵值；
• 桶排序：每個(gè)桶存儲(chǔ)一定范圍的數(shù)值；

總結(jié)

這次總結(jié)了10個(gè)經(jīng)典的排序算法，也算是給自己早年偷的懶補(bǔ)一個(gè)補(bǔ)丁吧。一些常用的算法在面試中也算是一個(gè)考察方向，但是一般考察都是時(shí)間復(fù)雜度低的那幾個(gè)即時(shí)間復(fù)雜度為O(nlogn)的：快速排序、堆排序、希爾排序。所以這幾個(gè)要熟練掌握，起碼要知道是怎樣的實(shí)現(xiàn)邏輯（畢竟面試也有口述算法的時(shí)候）。

畫圖：AlgorithmMan