1. 分而治之的概念     

         分而治之是一種使用遞歸解決問題的算法，主要的技巧是將一個大的復(fù)雜的問題劃分為多個子問題，而這些子問題可以作為終止條件，或者在一個遞歸步驟中得到解決，所有子問題的解決結(jié)合起來就構(gòu)成了對原問題的解決

    2.  分而治之的優(yōu)點和缺點

        分而治之算法通常包括一個或者多個遞歸方法的調(diào)用，當(dāng)這些調(diào)用將數(shù)據(jù)分隔成為獨立的集合從而處理較小集合的時候，分而治之的策略將會有很高的效率，而在數(shù)據(jù)進(jìn)行分解的時候，分而治之的策略可能會產(chǎn)生大量的重復(fù)計算，從而導(dǎo)致性能的降低。

    3.  畫標(biāo)尺程序的分析講解

         畫標(biāo)尺是分而治之的策略的一個簡單應(yīng)用，標(biāo)尺是由長度為1英寸的單元構(gòu)成的序列，每個單元的末端有最長的記號，每個寸單元的1/2英寸處的記號要比末端的短，在1/4處的記號比1/2的要短，1/8處比1/4處短，編寫一個程序，在一條線上，用規(guī)則間隔來繪制標(biāo)記，在特定位置有特定大小的記號。

         分析：在一個直線上，我們可以首先將這條直線一分為二,然后對分出來的二個再進(jìn)行拆分。直到滿足一定的精度要求，比如以最小刻度為1/8英寸為例，drawRuler作為畫標(biāo)尺的第歸函數(shù)，在drawRuler函數(shù)中用一段線段的兩端(起點（startPos），終點(endPos))，和變量h作為參數(shù),標(biāo)記的基礎(chǔ)高度為baseHeight，

而標(biāo)記的高度應(yīng)該為h*baseHeight,則標(biāo)尺的畫法可以分析如下：

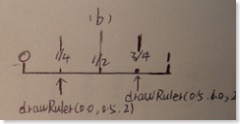
       計算間隔（0.0，1.0）的中點：midPos = (startPost+endPos)/2;在中點1/2處畫一個標(biāo)記，高度為3*baseHeight

       將中點分隔開的為兩條直線，再使用第歸函數(shù)drawRule，對應(yīng)的起點，終點為（0.0，0.5）和(0.5,1.0)，參數(shù)h-1,這樣可以使高度相比短些

      第歸步驟2（h＝2）

      midPos = (0.0+0.5)/2   (1/4處)，高度為 2*baseHeight

      midPos = (0.5+1.0)/2   (3/4處）高度為 2*baseHeight

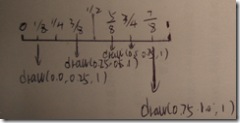
     第歸步驟（h=1）

     分別在1/8處和7/8處標(biāo)記，計算方法

      midPos = (0.0+0.25)/2  (1/8)    高度為baseHeight

      midPos = (0.75+1)/2  (7/8)     高度為baseHeight

    用圖示可以表示如下

      我們可以將連續(xù)第歸產(chǎn)生的記號看作二叉樹的節(jié)點。樹根h為初值。就是1/2處的記號，每個父記號都產(chǎn)生了兩個子記號。如下圖所示

    4.  可執(zhí)行程序文件

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Text;
using System.Windows.Forms;

namespace DrawRuler
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        private void Form1_Load(object sender, EventArgs e)
        {
        }

        void drawRuler(float startPos, float endPos, int h)
        {
            float baseHeight =4;
            if (h > 0)
            {
                float midPos = (startPos + endPos) / 2;
                float height = h * baseHeight;
                drawMark(midPos, height);
                drawRuler(startPos, midPos, h - 1);
                drawRuler(midPos, endPos, h - 1);
            }
        }

        void drawMark(float pos, float height)
        {
            using (Graphics g = this.CreateGraphics())
            {
                float xOffset = 100 + pos;
                float yOffset = 100-height;
                SolidBrush brusuh = new SolidBrush(Color.Black);
                Pen p = new Pen(brusuh, 1);
                g.DrawLine(p, xOffset, yOffset, xOffset, 100);
            }
        }
        private void Form1_Paint(object sender, PaintEventArgs e)
        {
            #region 首先畫一條直線
            using (Graphics g = e.Graphics)
            {
                float xOffset = 100;
                float yOffset = 100;
                int len = 300;
                SolidBrush brusuh = new SolidBrush(Color.Black);
                Pen p = new Pen(brusuh, 2);
                g.DrawLine(p, xOffset, yOffset, xOffset + len, yOffset);
            }
            #endregion

            drawRuler(0, 300, 3);
        }
    }
}

/Files/jillzhang/DrawRuler.rar

  5.  學(xué)習(xí)總結(jié)

       此系列是第歸算法的學(xué)習(xí)系列，全部內(nèi)容來源于課本，不是原創(chuàng)。只是程序為個人實現(xiàn)。大家想更詳細(xì)了解內(nèi)容，可以參考數(shù)據(jù)結(jié)構(gòu)C++描述

-------------------------------------------------------
人老了，腦袋不好用了，偶爾用算法來練練腦子，可以防止早衰。呵呵
                                                        jillzhang jillzhang@126.com