【模板】并查集

　　并查集是解決兩元素是否屬于同一集合，將一個集合合并另一集合的數(shù)據(jù)結(jié)構(gòu)。具體來說，我們使用數(shù)字代替集合，比如集合1，集合2.使用數(shù)組f[i]維護元素i屬于的集合，比如f[2] = 4表示元素2屬于集合4。具體我們有以下實現(xiàn)功能的代碼

1 初始化表示集合的數(shù)組。

    cin>>n>>m;
    for(int i=1; i<=n; i++)
        f[i]=i;

　　表示元素i屬于集合i，也就是說開始每個元素都是散開的。

2 實現(xiàn)查找功能的find()函數(shù)

int find(int x)
{
    if(f[x]!=x) return f[x]=find(f[x]);
    return x;
};

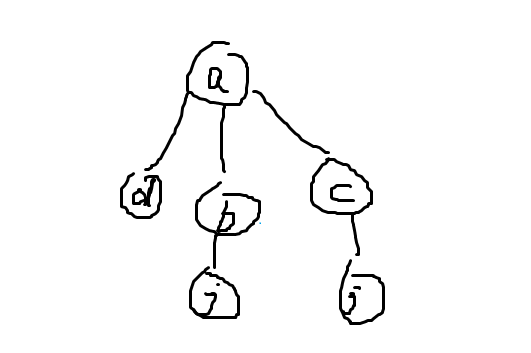
具體說明以下怎么實現(xiàn)的查找到的根結(jié)點（圖有點丑）

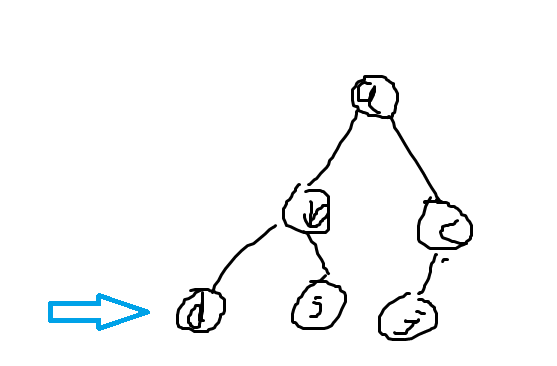
以結(jié)點d為例，假設(shè)我們查找結(jié)點d屬于那個集合也就是查找到這顆樹的根結(jié)點。

從系統(tǒng)棧層面解釋。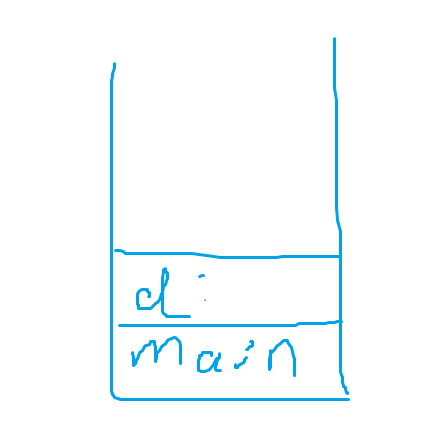

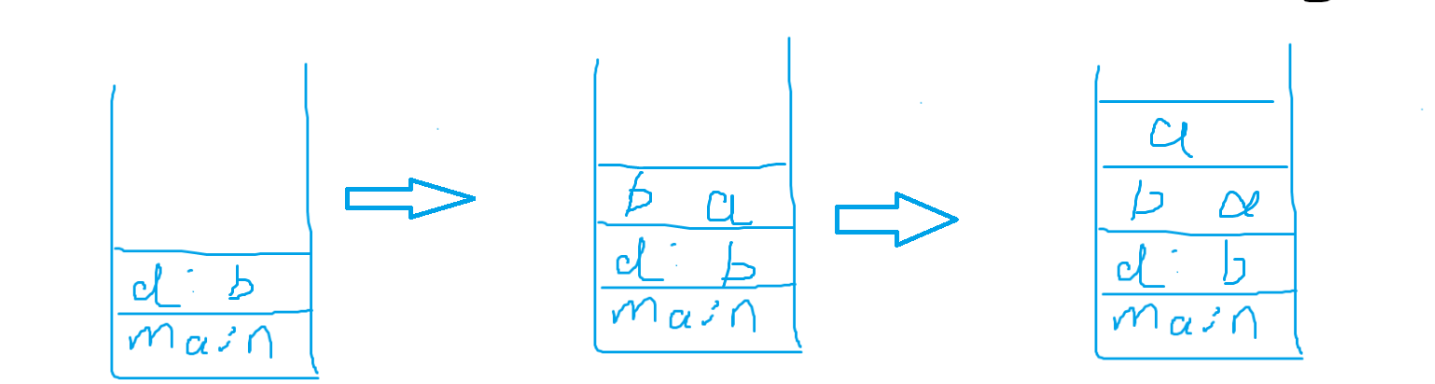
可以看到到達結(jié)點a之后，返回棧開始返回。

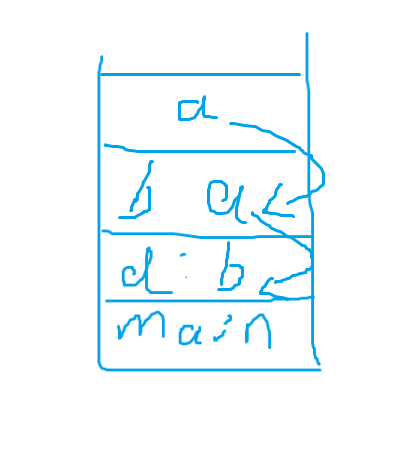
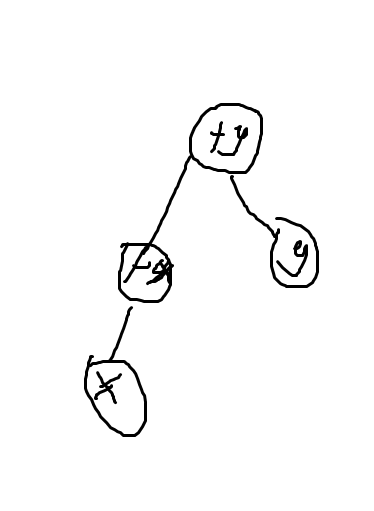
結(jié)點a從上到下賦值給路徑上的所有結(jié)點。那么這棵樹就變成這樣。

這就是路徑壓縮。

3 合并函數(shù)join()

void join (int x,int y)
{
    int fx=find(x),fy=find(y);
    if(fx!=fy)     f[fx]=fy;
};

　　假設(shè)合并元素x，y所在集合首先find(x),find(y)找到元素x，元素y屬于那個集合。

　然后將f[fx] 賦值為 fy，也就是x所在集合加入y所在集合。

實現(xiàn)了合并。

4 維護特征的并查集（帶權(quán)并查集）

　　例題：837. 連通塊中點的數(shù)量 https://www.acwing.com/problem/content/839/

　　只需要多增加一個數(shù)組siz[]來儲存集合i的大小即可。初始化siz[i] = 1;

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn = 1e5 + 10;
int n,m;

int f[maxn],size_f[maxn];

int find(int x){
    if(f[x] != x) return f[x] = find(f[x]);
    else return f[x];
}

void join(int x,int y){
    int x1 = find(x),y1 = find(y);
    if(x1 != y1) {
        size_f[y1] += size_f[x1]; // 主要維護集合fy的大小。
        f[x1] = y1;
    }
}
signed main ()
{
    cin>>n>>m;
    
    for(int i = 1; i<= n; i++){
        f[i] = i;
        size_f[i] = 1;
    }
    while(m--){
        string op;
        cin>>op;
        if(op == "C"){
            int a,b;
            cin>>a>>b;
            join(a,b);
        }else if(op == "Q1"){
            int a,b;
            cin>>a>>b;
            printf(find(a) == find(b) ? "Yes\n":"No\n");
        }else if(op == "Q2"){
            int a;
            cin>>a;
            printf("%d\n",size_f[find(a)]);
        }
    }
    return 0;
}

posted @ 2024-01-25 13:05 意外路過的番茄醬騎士閱讀(47) 評論(0) 收藏舉報

刷新頁面返回頂部

jiangjlon

【模板】并查集

公告