牛客編程巔峰賽S1第8場

翻滾吧牛牛(一)

牛牛有一個邊長為1的正六邊形，只要牛牛一推它就可以一直滾下去，正六邊形左下角為A，牛牛想知道正六邊形翻滾k次A點的軌跡邊長是多少呢。如圖是正六邊形翻滾一次的情況。給定正六邊形翻滾次數k，求A點翻滾軌跡長度

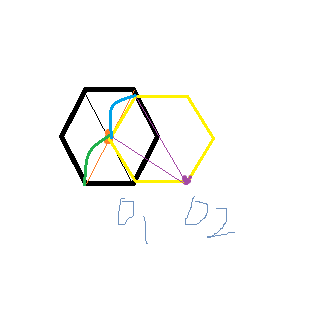
第一次旋轉 πr/3，第二次旋轉 √3πr/3，第三次旋轉 2πr/3...以此類推

class Solution {
public:
    /**
     * 
     * @param k int整型 翻滾次數
     * @return double浮點型
     */
    double circumference(int k)
{
    double r[5]={1,sqrt(3),2,sqrt(3),1};
    double l=0;
    for(int i=0;i<k;i++)
    {
        l+=r[i%6]*acos(-1)/3.0;
    }
    return l;
}
};

牛牛的分配

在牛牛面前有

因為牛牛是個完美主義者，他希望瓶子中的水能夠滿足他的要求，他的要求是瓶子中的水最少為

牛牛的分配規則是：每次可以選擇多個瓶子，將里面的水平均分配到已選擇的瓶子中。

給定

思路

把原來的vector排個序，從大到小看，如果當前的水瓶中的水量大于x，s++，并且將多余的水分給下一個水瓶。

 class Solution {
public:
    /**
     * 返回重新分配后，滿足牛牛要求的水量的瓶子最多的數量
     * @param n int整型 瓶子的數量
     * @param x int整型 牛牛的對瓶中的水量要求
     * @param a int整型vector 每個瓶子中的含水量
     * @return int整型
     */
    int solve(int n,int x,vector<int> &a)
{
    sort(a.begin(),a.end());
    int i,s=0;
    for(i=a.size()-1;i>0;i--)
    {
        if(a[i]>=x)
        {
            s++;
            a[i-1]+=a[i]-x;
        }
    }
    if(a[0]>=x)
        s++;
    return s;
}
};

牛牛構造等差數列

牛牛和牛妹在玩一個游戲，在他們面前有n個數，他們對每個數可以進行 +1 或 -1 操作，但對于每一個數，該操作最多只能執行一次。

游戲勝利的目標是：使用最少的操作次數，將這幾個數構造成一個等差數列。

牛牛特別想贏得游戲，所以他想讓你幫他寫一個程序，得出最少多少次操作后能使這幾個數變成一個等差數列，當然，如果完全不能構造成功，就輸出-1。

class Solution {
public:
    /**
     * 返回最少多少次操作后能使這幾個數變成一個等差數列，如果完全不能構造成功，就返回-1
     * @param n int整型 代表一共有n個數字
     * @param b int整型vector 代表這n個數字的大小
     * @return int整型
     */

int solve(int n, vector<int>& b)
{
    if(n<=2)
        return 0;
        int s=0x7fffffff;
        for(int i=-1;i<=1;i++)
        {
            for(int j=-1;j<=1;j++)
            {
                int first=b[0]+i;
                int second=b[1]+j;
                int d=first-second;
                int now=second;
                int cnt=abs(i)+abs(j);
                for(int k=2;k<n;k++)
                {
                    now-=d;
                    if(abs(now-b[k])<=1)
                        cnt+=abs(now-b[k]);
                    else
                        break;
                    if(k==n-1)
                        s=min(cnt,s);
                }
            }
        }
    if(s<0x7fffffff)
        return s;
        return -1;
}
};

playfair

牛牛想給牛妹寫信，但是牛牛怕信中的信息泄露出去，于是用playfair加密信息。加密過程中的j都由i來代替。playfair加密算法首先需要繪制密碼表，密碼表是一個5*5的矩陣，開始由密鑰按順序排列，其余按照未出現的字母順序。若密鑰中含有重復字母需要將重復字母去掉，若有j用i來代替，例如密鑰為nowcoder，得到的密碼表為

加密明文需要符合以下規則：

將明文中每兩個字母組成一對，若成對后是兩個相同字母或留下一個字母無法成對，則不進行變化直接放入密文中
明文對p₁p₂在同一行，對應密文對c₁c₂分別為緊靠p₁p₂右端的字母，最后一列右端對應第一列。例如明文對為rf，對應密文對為ae
明文對p₁p₂在同一列，對應密文對c₁c₂分別為緊靠p₁p₂下方的字母，最后一行下方對應第一行。例如明文對為rv，對應密文對為ho
明文對p₁p₂不在同一行且不在同一列，對應密文對c₁c₂分別為p₁p₂確定的矩形中的同行另外兩角，例如明文對為hb，對應密文對為kr

現在牛牛告訴你密鑰和明文你能告訴牛牛密文是什么嗎？

posted @ 2020-08-02 10:49 Drophair 閱讀(313) 評論(0) 收藏舉報

刷新頁面返回頂部

Drophair

GitHub：https://github.com/drophair

牛客編程巔峰賽S1第8場

公告