馬拉車法求解最長回文子串，優化中心擴展法，統一奇偶處理，利用對稱性減少重復計算，時間復雜度O(n)，空間復雜度O(n)。

書接上回，我們今天繼續來聊聊最長回文子串的馬拉車解法。

題目：給你一個字符串 s，找到 s 中最長的回文子串。

01、中心擴展法優化-合并奇偶處理

俗話說沒有最好只有更好，看著O(n^2)的時間復雜度，想想應該還有更優的方案吧，答案是肯定的，馬拉車法就可以做到時間和空間復雜度都是O(n)。

其實無論什么算法都是為了解決某種問題而產生的，因此我們還是循序漸進的來優化中心擴展法最終得到馬拉車法。

我們知道在中心擴展法中有一個很明顯的問題：回文串長度奇偶性需要不同的處理方式，并且在計算之前我們也不知道這個回文串到底是奇還是偶，導致每次我們都需要同時求出奇偶兩種情況下的回文串并取最大的那個，因此我們需要首先解決奇偶性導致的差異化處理問題。

如果要解決這個問題可能要從兩個方面入手：其一從外部下手找到一個公式統一奇偶性，其二從內部下手修改自身使其變的統一。

關于第一點，因為本題的特點是根據奇偶性做不同的處理，而統一的公式更偏向一個值可以是奇或偶最后得到統一的結果，比如7和8，(7-1)/2=3，(8-1)/2=3，因此第一點并不適合本題。

關于第二點，奇數個字符之間有偶數個空格，偶數個字符之間有奇數個空格，而奇數加偶數還是奇數，也就是如果我們把這些空格考慮進來，奇偶性就統一了，那么接下來還有分析一下這個空格引入后是否會對原回文串特性產生影響，其實并沒有影響，對于奇數串相當于中心元素兩邊各多了一個空格還是對稱的，對于偶數相當于中心的兩個元素之間加了一個空格結果也還是對稱的，因為空格比較特殊，我們選擇一個其他特殊符號比如[#]，因此這個方案具有可行。

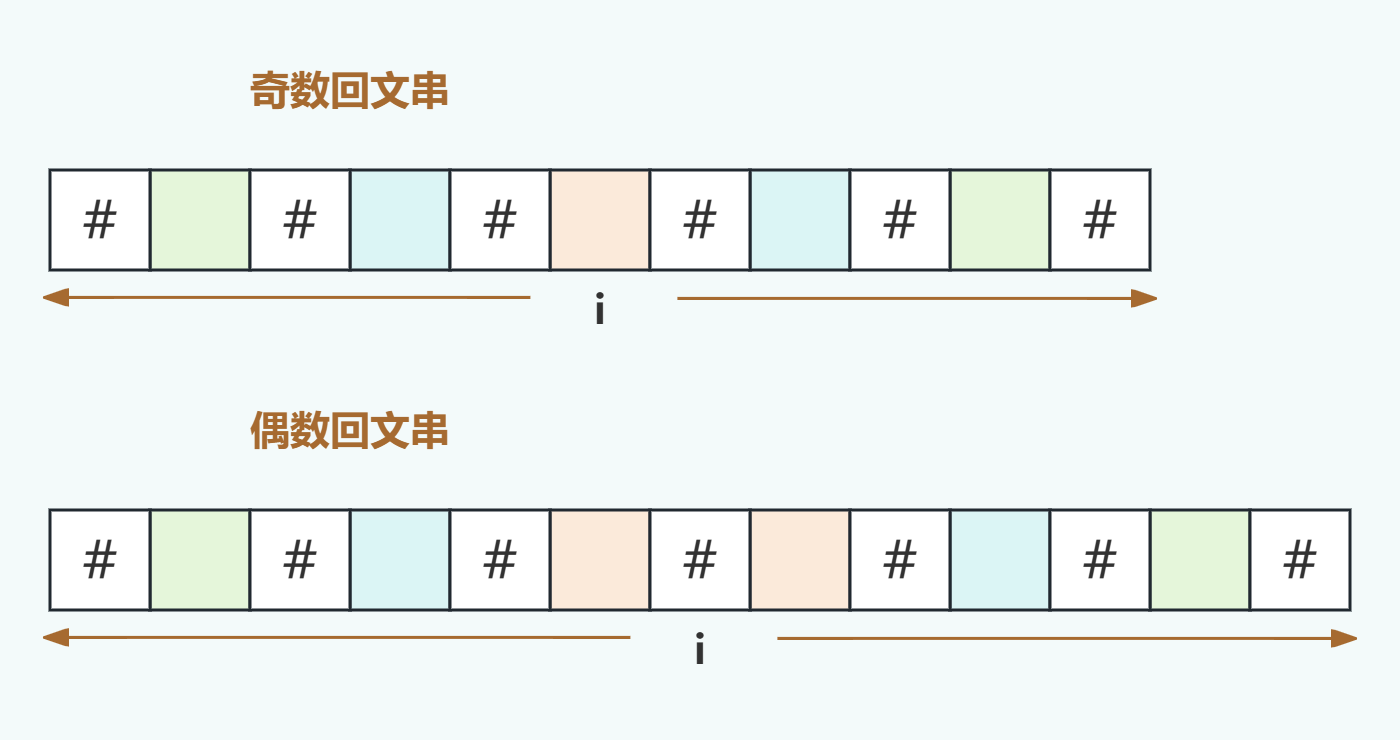
這個方案還有最后一個小問題，就是怎么計算回文串長度，即實現通過處理后的字符串計算出實際的字符長度。

比如上圖中原奇數回文串長度是5，處理后長度是11，原偶數回文串長度是6，出來后是13，如果我們不考慮中心元素i，則回文串實際長度正好等于處理后的一半，即原回文串長度=（處理后回文串長度 - 1）/2，我們先給這個值取個名字方便后面交流，叫回文串半徑。

到這里優化方案就是確定了，解決了奇偶性問題，解決了字符串處理后轉換問題，下面我們看看具體實現代碼。

//中心擴散法-合并奇偶
public static string CenterExpandMergeOddEven(string s)
{
    //如果字符串為空或只有一個字符，直接返回該字符串
    if (s == null || s.Length < 1)
    {
        return "";
    }
    // 預處理字符串，插入#字符以統一處理奇偶回文串
    //比如：s="cabac"轉化為s="#c#a#b#a#c#"
    var tmp = $"#{string.Join("#", s.ToCharArray())}#";
    //記錄最長回文子串的起始位置和最大長度
    var startIndex = 0;
    var maxLength = 0;
    //從左到右遍歷處理過的字符串，求每個字符的回文串半徑
    for (var i = 0; i < tmp.Length; ++i)
    {
        //計算當前以i為中心的回文串半徑
        var radius = PalindromicRadius(tmp, i, i);
        //如果當前計算的半徑大于maxLength，就更新startIndex
        if (radius > maxLength)
        {
            startIndex = (i - radius) / 2;
            maxLength = radius;
        }
    }
    //根據startIndex和maxLength，從原始字符串中截取返回
    return s.Substring(startIndex, maxLength);
}
//回文串半徑
public static int PalindromicRadius(string s, int leftIndex, int rightIndex)
{
    //左邊界大于等于首字符，右邊界小于等于尾字符，并且左右字符相等
    while (leftIndex >= 0 && rightIndex < s.Length && s[leftIndex] == s[rightIndex])
    {
        //從中心往兩端擴展一位
        //向左擴展
        --leftIndex;
        //向右擴展
        ++rightIndex;
    }
    //返回回文串半徑（注意本來應該是（rightIndex - leftIndex + 1）/2，
    //但是滿足條件后leftIndex、rightIndex又分別向左和右又各擴展了一位，
    //因此需要把這兩位減掉，因為中心元素不在計算返回還需要減掉一位，
    //因此（rightIndex - leftIndex + 1 - 2 - 1）/2
    //所以最后公式為（rightIndex - leftIndex - 1）/2）  
    return (rightIndex - leftIndex - 2) / 2;
}

時間復雜度：O(n^{2)，由于每遍到一個字符，都需要往左/右進行探測，所以是O(n}2)。

空間復雜度：O(1)。

因此這次優化性能上并沒有任何提升，只是處理方式上做了優化，這一步并不是白做，而是為了下面馬拉車法做前期準備。

02、中心擴展法再優化（馬拉車法）

再暴力破解法優化中我們用到了經典的以空間換時間的做法，把已經計算過的子字符串結果存儲下來減少了不必要的計算，同樣的我也可以用類似的思想來優化中心擴展法。

暴力破解法用了回文串對稱性由外向內判斷是否是回文串，中心擴展法用了回文串對稱性由內向外判斷是否是回文串，而這兩種方法都是應用了對稱性去算，那么我們能否直接用回文串的對稱性直接判斷是否為回文串呢？答案是肯定的，下面我們用圖例來說明其中原理。

在上面的合并奇偶處理中，我們知道處理后回文串半徑長度就是我們最終回文串長度。如果我們把已經計算過的回文串半徑存儲下來，后面需要的時候就可以直接拿過來用了。

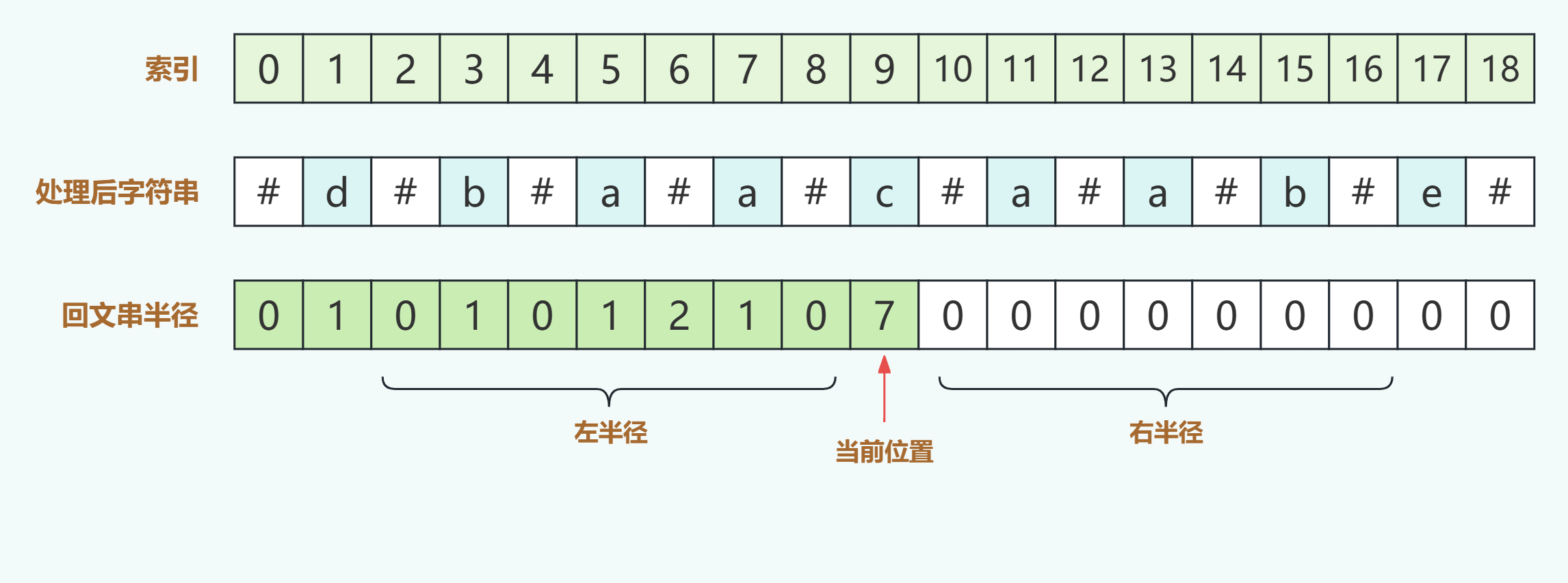
如上圖，在回文串半徑行中，綠色背景表示已經計算完回文串半徑的字符，并中心擴展是從左往右計算的，此時計算完了s[9]即字符c處，那么我們想象一下此時如何計算索引為10即s[10]元素的回文串半徑呢？s[11]、s[12]呢？

回想一下上文提到的對稱性，如果我們以當前位置s[9]為中心點，那么其右半徑和其左半徑是對稱的，也就是說相對應的元素應該是性質相同的，可以合理猜測s[10]應該和s[8]的回文串半徑一致也為0，同理猜測s[11]=s[7]=1，s[12]=s[6]=2。

當然這并不絕對，我們只是想拿來說明我們可以利用對稱性，把其對稱點已經計算過的結果利用上，雖然上面的s[10]，s[11]，s[12]三個值是對的，但描述并不準確，因為存在s[10]>s[8]的情況。如下圖：

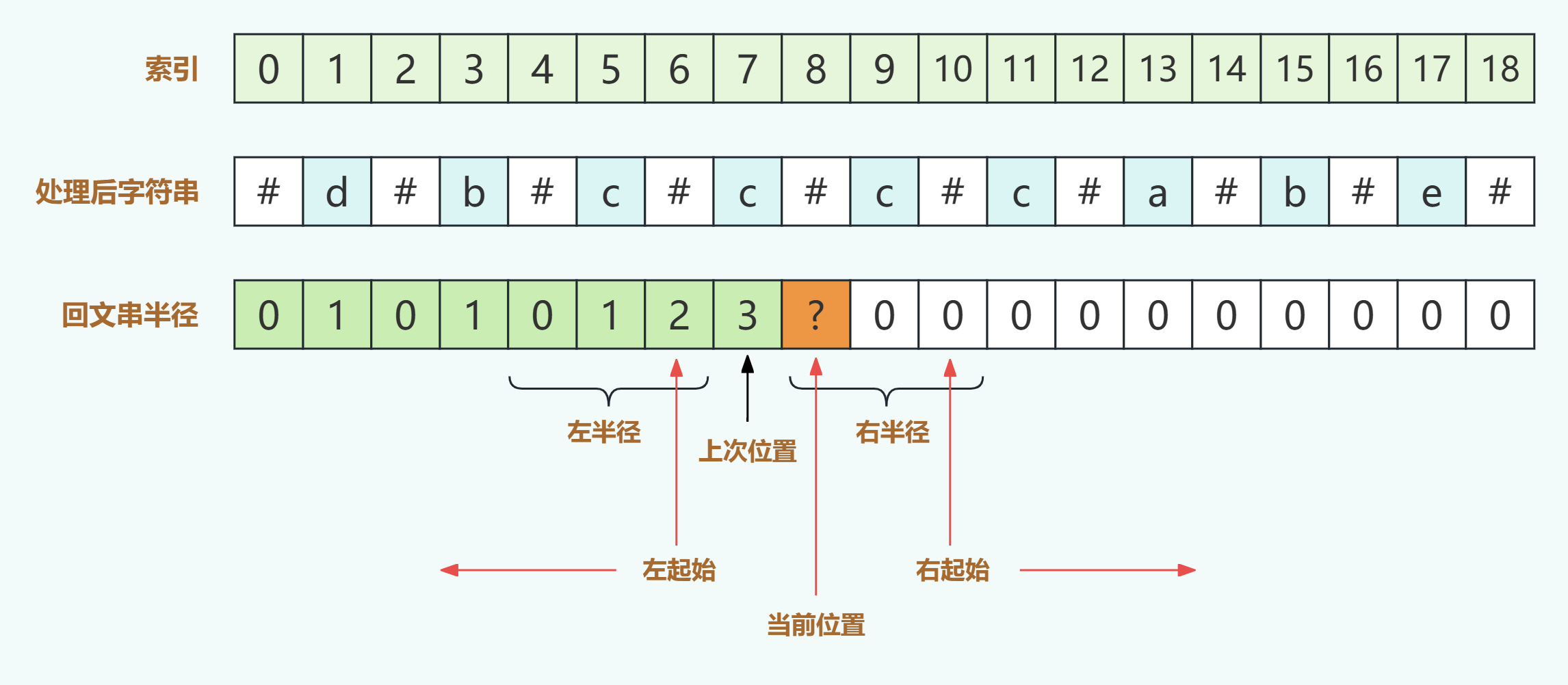
如上圖，當上一次處理完s[7]，可得其回文串半徑為3，此時開始計算s[8],使用對稱性可得s[8]>=s[6],因此我們在計算以s[8]為中心向兩邊擴展查找回文串時不需要再以s[8]為起點了，而是根據s[6]=2,我們直接跳躍2位，左邊從s[6],右邊從s[10],開始向兩邊擴展查找以s[8]為中心的實際回文串長度，最后計算可能為4，這一步正是整個算法的核心所在。

因此我們可以把這個算法分為兩種情況：

（1）當前位置大于當前已探測右側最遠位置，則直接使用中心擴展方法查找回文串；

（2）當前位置小于等于當前已探測右側最遠位置，則根據其對稱位置已計算結果，進行直接選擇跳過部分位再開始使用中心擴展方法查找回文串；

當然起始位置、已探測最右側位置、中心點、最大長度怎么選，什么時候更新，跳過多少位后再計算，這些都是細節部分了，我們下面直接看代碼。

//馬拉車法
public static string Manacher(string s)
{
    if (s == null || s.Length == 0)
    {
        return "";
    }
    var tmp = $"#{string.Join("#", s.ToCharArray())}#";
    //rightIndex表示目前計算出的最右端范圍，rightIndex和左邊都是已探測過的
    var rightIndex = 0;
    //centerIndex最右端位置的中心對稱點
    var centerIndex = 0;
    //記錄最長回文子串的起始位置和最大長度
    var startIndex = 0;
    var maxLength = 0;
    //radiusPoints數組記錄所有已探測過的回文串半徑，后面我們再計算i時，根據radiusPoints[iMirror]計算i
    var radiusPoints = new int[tmp.Length];
    //從左到右遍歷處理過的字符串，求每個字符的回文串半徑
    for (var i = 0; i < tmp.Length; i++)
    {
        //根據i和right的位置分為兩種情況：
        //1、i<=right利用已知的信息來計算i
        //2、i>right，說明i的位置時未探測過的，只能用中心探測法
        if (i <= rightIndex)
        {
            // 找出i關于前面中心的對稱
            var iMirror = 2 * centerIndex - i;
            //這句是關鍵，不用再像中心探測那樣，一點點的往左/右擴散，
            //根據已知信息減少不必要的探測，必須選擇兩者中的較小者作為左右探測起點
            var minRadiusLength = Math.Min(rightIndex - i, radiusPoints[iMirror]);
            //這里左右-1和+1是因為對稱性可以直接跳過相應的回文串半徑
            radiusPoints[i] = PalindromicRadius(tmp, i - minRadiusLength - 1, i + minRadiusLength + 1);
        }
        else
        {
            //i落在rightIndex右邊，是沒被探測過的，只能用中心探測法
            //這里左右-1和+1，是因為中心點字符肯定是回文串，可以直接跳過
            radiusPoints[i] = PalindromicRadius(tmp, i - 1, i + 1);
        }
        //大于rightIndex，說明可以更新最右端范圍了，同時更新centerIndex
        if (i + radiusPoints[i] > rightIndex)
        {
            centerIndex = i;
            rightIndex = i + radiusPoints[i];
        }
        //找到了一個更長的回文半徑，更新原始字符串的startIndex位置
        if (radiusPoints[i] > maxLength)
        {
            startIndex = (i - radiusPoints[i]) / 2;
            maxLength = radiusPoints[i];
        }
    }
    //根據start和maxLen，從原始字符串中截取一段返回
    return s.Substring(startIndex, maxLength);
}
//回文串半徑
public static int PalindromicRadius(string s, int leftIndex, int rightIndex)
{
    //左邊界大于等于首字符，右邊界小于等于尾字符，并且左右字符相等
    while (leftIndex >= 0 && rightIndex < s.Length && s[leftIndex] == s[rightIndex])
    {
        //從中心往兩端擴展一位
        //向左擴展
        --leftIndex;
        //向右擴展
        ++rightIndex;
    }
    //返回回文串半徑（注意本來應該是（rightIndex - leftIndex + 1）/2，
    //但是滿足條件后leftIndex、rightIndex又分別向左和右又各擴展了一位，
    //因此需要把這兩位減掉，因為中心元素不在計算返回還需要減掉一位，
    //因此（rightIndex - leftIndex + 1 - 2 - 1）/2
    //所以最后公式為（rightIndex - leftIndex - 1）/2）  
    return (rightIndex - leftIndex - 2) / 2;
}

時間復雜度：O(n)，可能比較難以理解的是為什么for嵌套了while還是O(n)的時間復雜度？因為首先每個字符最多只會進行一次擴展，其次當進行一次新的擴展后，當前位置到最新的有邊界這部分可以通過對稱性得到而不需要再次擴展，因此while總的操作次數不會大于n，再加上預處理字符串n，以及初始化的輔助數組2n+1，因此整體還是O(n)。

空間復雜度：O(n)，我們需要 O(n) 的空間記錄每個位置的半徑。

這就是馬拉車算法的整個過程，我們再來總結一下，馬拉車算法是對中心擴展法的優化，解決了其兩個問題：其一奇偶統一處理，其二利用對稱性減少重復計算。其中第二點的重點是通過對稱性不用每次擴展都從中心點出發，而是直接跳過已計算的部分位。

注：測試方法代碼以及示例源碼都已經上傳至代碼庫，有興趣的可以看看。https://gitee.com/hugogoos/Planner