LeetCode題集-5 - 最長(zhǎng)回文子串(一)
題目:給你一個(gè)字符串 s,找到 s 中最長(zhǎng)的回文子串。

這一題作為中等難度,常規(guī)解法對(duì)于大多數(shù)人應(yīng)該都沒有難度。但是其中也有超難的解決辦法,下面我們就一起由易到難,循序漸進(jìn)地來(lái)解這道題。
01、暴力破解法
對(duì)于大多數(shù)題目來(lái)說(shuō),在不考慮性能的情況下,暴力破解法常常是最符合人的思維習(xí)慣的。
比如這道題,求一個(gè)字符串中最長(zhǎng)的回文子串,那么我們只需要把字符串中所有可能的子字符串都判斷一下是不是回文串,并找出長(zhǎng)度最長(zhǎng)的不就行了嘛。
這里需要三層循環(huán),第一層和第二層循環(huán)組織出所有可能的子字符串,第三層循環(huán)判斷是否為回文串。
而判斷一個(gè)字符串是否為回文串,也很簡(jiǎn)單,只需要從字符串兩端開始判斷首尾字符是否相等,如果相等繼續(xù)向字符串中心方向前進(jìn)繼續(xù)比較下一個(gè)首尾字符是否相等,直到比較完所有字符,如果都相等則為回文串。其核心思想是由外向內(nèi),逐一比較。
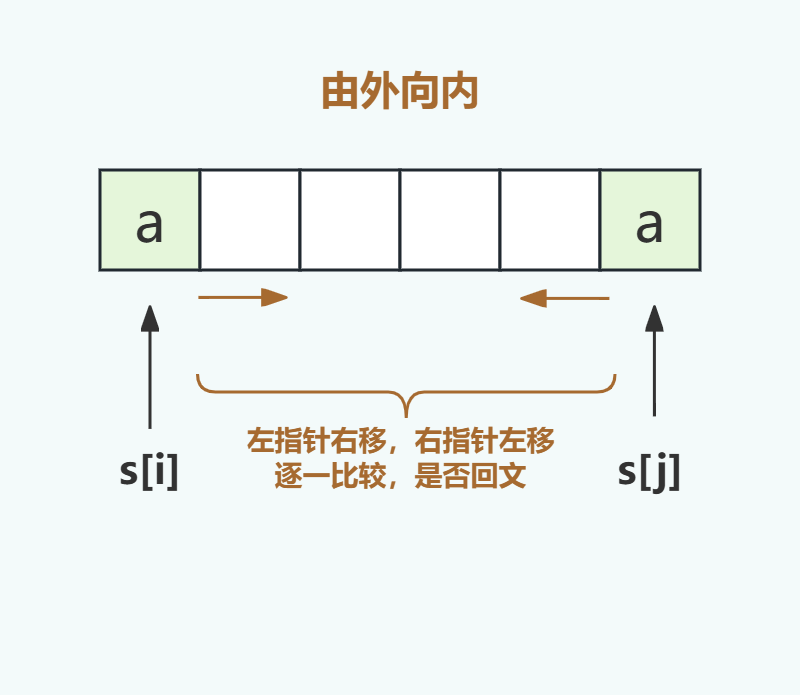
具體代碼如下:
//暴力破解法
public static string BruteForce(string s)
{
var result = string.Empty;
var max = 0;
var len = s.Length;
//從第一個(gè)字符開始遍歷,作為起始字符
for (var i = 0; i < len; i++)
{
//從第二個(gè)字符來(lái)開始遍歷,作為結(jié)束字符
for (var j = i + 1; j <= len; j++)
{
//取出[i,j)字符串,即包含i,不好含j,為臨時(shí)字符串
var temp = s[i..j];
//如果臨時(shí)字符串是回文字符串,且臨時(shí)字符串長(zhǎng)度大于目標(biāo)字符串長(zhǎng)度
if (IsPalindromic(temp) && temp.Length > result.Length)
{
//則更新目標(biāo)字符串為當(dāng)前臨時(shí)字符串
result = temp;
max = Math.Max(max, j - i - 1);
}
}
}
return result;
}
//判斷字符串是否為回文串
public static bool IsPalindromic(string s)
{
var len = s.Length;
//遍歷字符串的一半長(zhǎng)度
for (var i = 0; i < len / 2; i++)
{
//如果對(duì)稱位置不同,則不為回文串
if (s[i] != s[len - i - 1])
{
return false;
}
}
return true;
}
時(shí)間復(fù)雜度:兩層for循環(huán)O(n^2),for 循環(huán)里邊判斷是否為回文串O(n),所以時(shí)間復(fù)雜度為O(n^3)。
空間復(fù)雜度:O(1),常數(shù)個(gè)變量。
02、暴力破解法優(yōu)化(動(dòng)態(tài)規(guī)劃法)
要想優(yōu)化暴力破解法,我們要先找到它到底有什么問題。它的時(shí)間復(fù)雜度之所以這么高,是因?yàn)橛写罅康闹貜?fù)計(jì)算,可能文字描述不夠直觀,下面我們先用二維表展示一個(gè)字符串的所有子字符串的組合情況,然后再在這個(gè)表中看判斷是否為回文串時(shí)哪些子字符串被重復(fù)判斷。
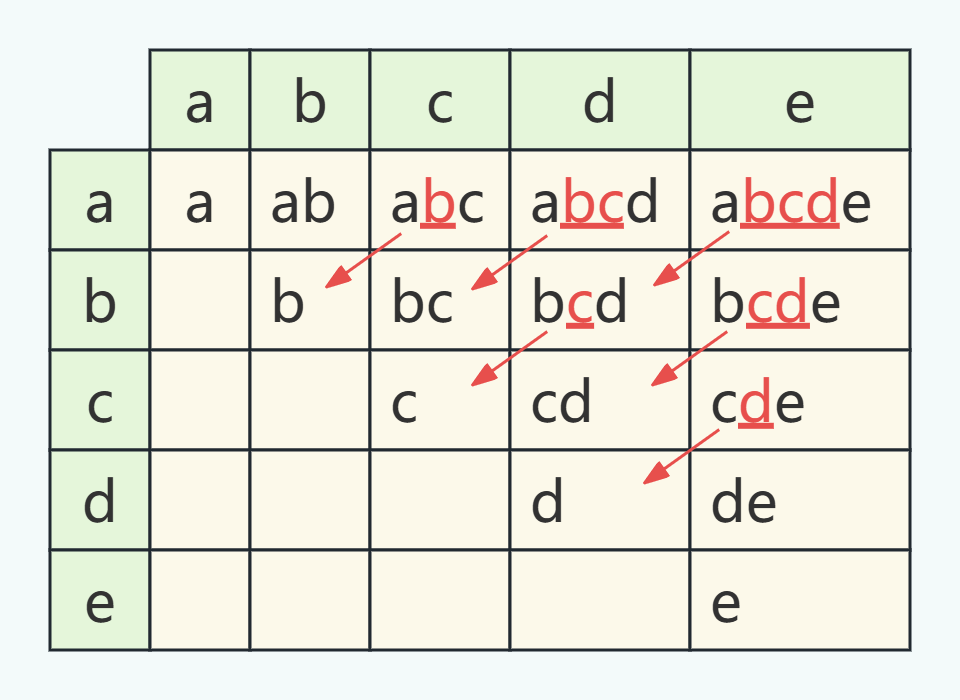
如上圖在字符串a(chǎn)bcde中,在判斷其子字符串bcd是否是回文串時(shí),作為字符串bcd已經(jīng)計(jì)算過了,同樣的其子字符串c,作為字符串也已經(jīng)計(jì)算過了,其他的沿著箭頭方向都是表示存在重復(fù)計(jì)算的地方。
到這里我們的優(yōu)化方案就有了,我們可以把已經(jīng)計(jì)算過的存下來(lái),這樣下次用到的時(shí)候直接拿過來(lái)用而不用再計(jì)算了。
既然我們通過圖就發(fā)現(xiàn)了一些規(guī)律,我們不妨再深入思考一下,為什么會(huì)這樣?
如果我們基于暴力破解法中判斷是否為回文串的算法定義回文串,那么可得:
P(i,j)=P(i+1,j-1)&&S[i]==S[j]
可以理解為如果一個(gè)字符串是回文串,那么去掉首尾字符后子字符串依然是回文串。反過來(lái)如果子字符串是回文串并且其首尾一個(gè)字符相等,那么這個(gè)字符串整體也是回文串。
我們?cè)賹?duì)上圖斜對(duì)角上加些輔助線,如果我們按所有子字符串的長(zhǎng)度分類,則會(huì)發(fā)現(xiàn)長(zhǎng)度為3的依賴長(zhǎng)度為1的,長(zhǎng)度為5的依賴長(zhǎng)度為3的,長(zhǎng)度為4的依賴長(zhǎng)度為2的。如下圖:
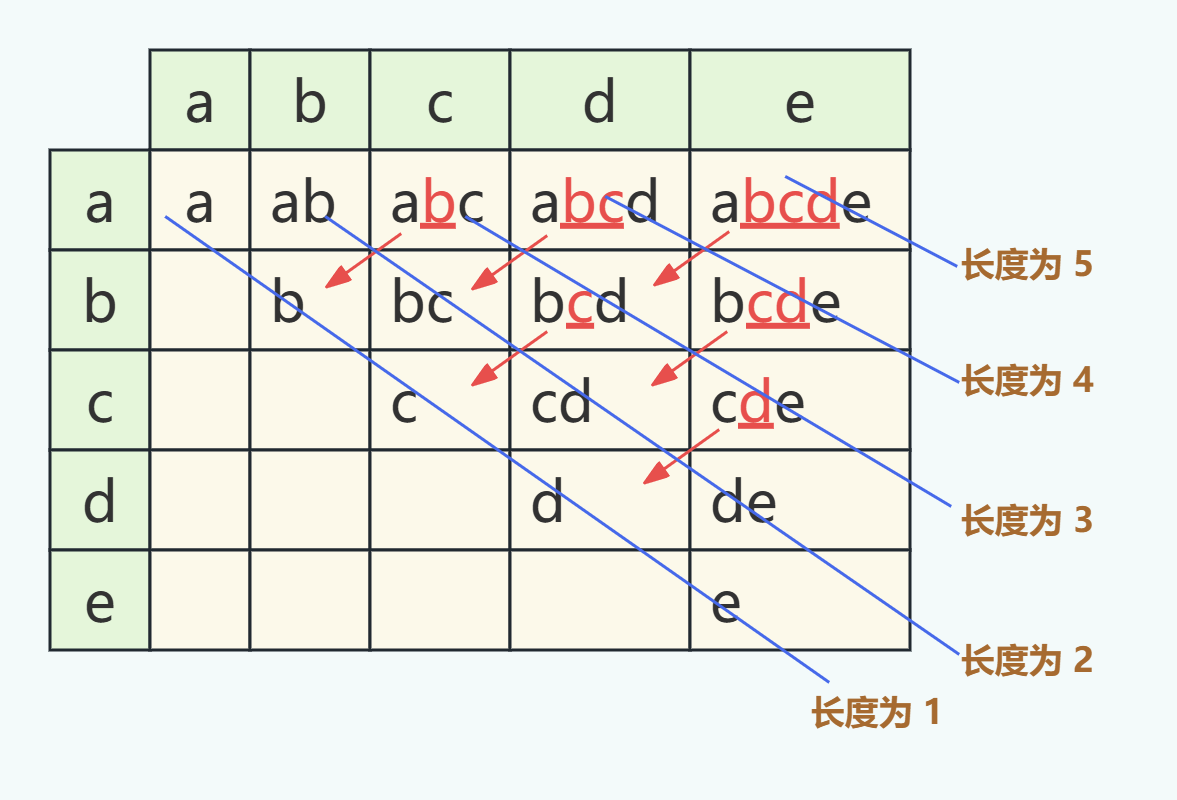
長(zhǎng)度為1本身就是回文串,長(zhǎng)度為2的如果兩個(gè)字符相等則為回文串,那么所有長(zhǎng)度大于等于3的都可以通過長(zhǎng)度為1和2的計(jì)算出來(lái)。
到這里整個(gè)算法思路就出來(lái)了:先計(jì)算長(zhǎng)度為1和2的子字符串并存入二維數(shù)組,然后基于此二維數(shù)組繼續(xù)計(jì)算長(zhǎng)度為3、4、5……。
具體代碼如下:
//動(dòng)態(tài)規(guī)劃
public static string DynamicProgramming(string s)
{
var length = s.Length;
//判斷該組合是否是回文字符串,行為起始點(diǎn),列為結(jié)尾點(diǎn)
var dp = new bool[length, length];
//最長(zhǎng)回文字符串,初始為0
var result = string.Empty;
//從回文長(zhǎng)度為1開始判斷,到字符長(zhǎng)度n為止
for (var len = 1; len <= length; len++)
{
for (var startIndex = 0; startIndex < length; startIndex++)
{
//結(jié)束索引 = 起始索引 + 間隔(len - 1)
var endIndex = startIndex + len - 1;
//結(jié)束索引超出字符串長(zhǎng)度,結(jié)束本次循環(huán)
if (endIndex >= length)
{
break;
}
//回文字符串的公式就是子字符串也是回文,并且當(dāng)前起始字符和結(jié)束字符相等,
//所以得出公式 dp[startIndex+1,endIndex-1] && s[startIndex] == s[endIndex]
//其中回文長(zhǎng)度為1和2兩種特殊情況需要單獨(dú)處理,其特殊性在于他們不存在子字符串
//回文長(zhǎng)度為1時(shí),自身當(dāng)然等于自身
//回文長(zhǎng)度為2時(shí),起始字符和結(jié)束字符是相鄰的,只要相鄰的字符相等就可以
dp[startIndex, endIndex] = (len == 1 || len == 2 || dp[startIndex + 1, endIndex - 1]) && s[startIndex] == s[endIndex];
//當(dāng)前字符串是回文,并且當(dāng)前回文長(zhǎng)度大于最長(zhǎng)回文長(zhǎng)度時(shí),修改result
if (dp[startIndex, endIndex] && len > result.Length)
{
result = s.Substring(startIndex, len);
}
}
}
return result;
}
時(shí)間復(fù)雜度:O(n^2),即為兩層for循環(huán)組成的所有子字符串情況。
空間復(fù)雜度:O(n^2),即存儲(chǔ)已計(jì)算子字符串結(jié)果需要的空間。
這個(gè)算法還有一個(gè)專有名稱:動(dòng)態(tài)規(guī)劃,我們這里之所以沒有突出去講,是想把整個(gè)解題思路展現(xiàn)出來(lái),掌握好了基礎(chǔ)解題能力,我們才能做總結(jié),而這個(gè)解法的總結(jié)就可以概括為動(dòng)態(tài)規(guī)劃,這是一種通用的思想,后面會(huì)經(jīng)常用到。
03、中心擴(kuò)展法
上面的優(yōu)化雖然時(shí)間復(fù)雜度降下來(lái)了,但是空間復(fù)雜度上升了,我們繼續(xù)想想有什么其他方法呢?
上面的方法判斷是否為回文串的核心思想是由外向內(nèi),那我們是否可以換個(gè)思路——從內(nèi)向外呢?這就是中心擴(kuò)展法的核心思想。
在暴力破解法中,我們需要兩層循環(huán)表示任何一種子字符串排列,而且中心擴(kuò)展法核心思想是通過一個(gè)中心點(diǎn)向兩邊擴(kuò)展也就天然只需要一層循環(huán)即可表示探測(cè)所有字符的情況。
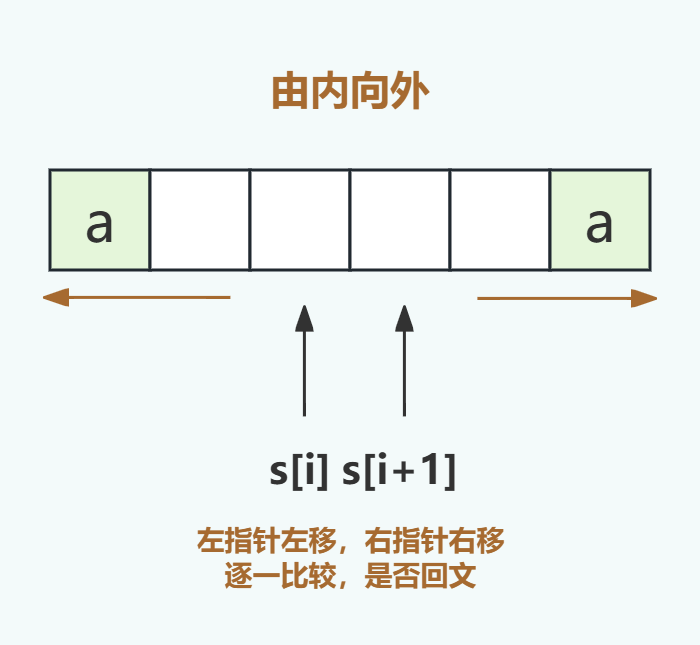
由中心往兩邊擴(kuò)展是對(duì)稱的,而回文串長(zhǎng)度可以是奇數(shù)也可以是偶數(shù),因此我們?cè)谥行臄U(kuò)展時(shí)就需要分奇偶兩種情況來(lái)處理。
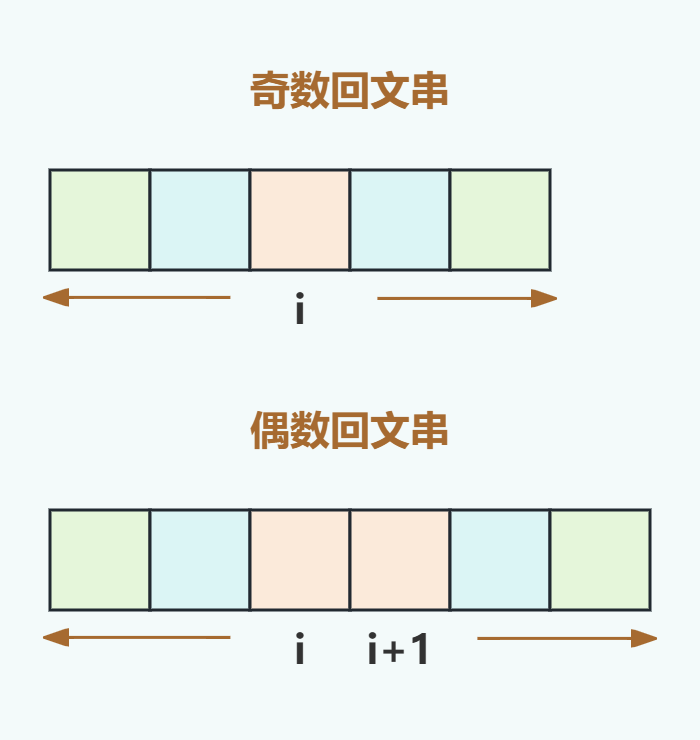
到這里我們可以大致梳理一下整體邏輯了:
(1)依次循環(huán)處理字符串的每個(gè)字符,向兩邊擴(kuò)展;
(2)每次擴(kuò)展分奇偶兩種情況處理;
(3)計(jì)算出最大長(zhǎng)度并保留;
(4)重復(fù)(2)、(3)直至所有字符處理完成;
具體實(shí)現(xiàn)代碼如下:
//中心擴(kuò)散法
public static string CenterExpand(string s)
{
//如果字符串為空或只有一個(gè)字符,直接返回該字符串
if (s == null || s.Length < 1)
{
return "";
}
//記錄最長(zhǎng)回文子串的起始位置和結(jié)束位置
var startIndex = 0;
var endIndex = 0;
//遍歷每個(gè)字符,同時(shí)處理回文字串長(zhǎng)度為奇偶的情況,
//即以該字符或該字符與其下一個(gè)字符之間為中心的回文
for (var i = 0; i < s.Length; i++)
{
//獲取回文字串長(zhǎng)度為奇數(shù)的情況,
//即以當(dāng)前字符為中心的回文長(zhǎng)度
var oddLength = PalindromicLength(s, i, i);
//獲取回文字串長(zhǎng)度為偶數(shù)的情況,
//即以當(dāng)前字符和下一個(gè)字符之間的空隙為中心的回文長(zhǎng)度
var evenLength = PalindromicLength(s, i, i + 1);
//取兩種情況下的最長(zhǎng)長(zhǎng)度
var maxLength = Math.Max(oddLength, evenLength);
//如果找到更長(zhǎng)的回文子串,更新起始位置和長(zhǎng)度
if (maxLength > endIndex - startIndex)
{
//重新計(jì)算起始位置
startIndex = i - (maxLength - 1) / 2;
//重新計(jì)算結(jié)束位置
endIndex = i + maxLength / 2;
}
}
//返回最長(zhǎng)回文子串
return s[startIndex..(endIndex + 1)];
}
//從中心向外擴(kuò)展,檢查并返回回文串的長(zhǎng)度
public static int PalindromicLength(string s, int leftIndex, int rightIndex)
{
//左邊界大于等于首字符,右邊界小于等于尾字符,并且左右字符相等
while (leftIndex >= 0 && rightIndex < s.Length && s[leftIndex] == s[rightIndex])
{
//從中心往兩端擴(kuò)展一位
//向左擴(kuò)展
--leftIndex;
//向右擴(kuò)展
++rightIndex;
}
//返回回文串的長(zhǎng)度(注意本來(lái)應(yīng)該是rightIndex - leftIndex + 1,
//但是滿足條件后leftIndex、rightIndex又分別向左和右又各擴(kuò)展了一位,
//因此需要把這兩位減掉,所以最后公式為rightIndex - leftIndex - 1)
return rightIndex - leftIndex - 1;
}
時(shí)間復(fù)雜度:O(n^2)。
空間復(fù)雜度:O(1)。
此方法雖然時(shí)間復(fù)雜度沒變,但是空間復(fù)雜度大大降低。這也給了我們繼續(xù)優(yōu)化的動(dòng)力。
下一章節(jié)我們將詳細(xì)講解次題的馬拉車解法。
注:測(cè)試方法代碼以及示例源碼都已經(jīng)上傳至代碼庫(kù),有興趣的可以看看。https://gitee.com/hugogoos/Planner



 浙公網(wǎng)安備 33010602011771號(hào)
浙公網(wǎng)安備 33010602011771號(hào)