算法學習：歸并排序

1、概念

歸并排序使用了二分法，歸根到底的思想還是分而治之。

拿到一個長數組，將其不停的分為左邊和右邊兩份，然后以此遞歸分下去。

將已有序的子序列合并，得到完全有序的序列;即先使每個子序列有序，再使子序列段間有序。若將兩個有序表合并成一個有序表，稱為二路歸并。

歸并排序是一種穩定的排序方法。

2、舉例

1）合并兩個有序數組，偽代碼

    arr_a = [1,4,5,6]
    arr_b = [4,4,8,10]
偽代碼如下：
    result = []
    idx_a,idx_b
    while idx_a<len(arr_a) and idx_b<len(arr_b):
        if arr_a[idx_a]<=arr_b[idx_b]:
            result[arr_a[idx_a]]
            idx_a+=1
        elif arr_a[idx_a]>arr_b[idx_b]
            result[arr_b[idx_b]]
            idx_b+=1
    if idx_a==len(arr_a):
        result.extend(arr_b[idx_b:])

2）對于沒有順序的數組排序

思想：拆拆拆，合合合

將一個無序的數組從數組的中間部分無限的拆分，形成前后兩部分（循環拆分）當我們拆分到數組只有一個元素的時候，這個數組就可以看作是一個有序數組，然后再將前后2個部分合并起來，這樣整個數組就有序了。

[11,2,3,43,23,5,6,9,10] len==9 mid =4
拆：拆分到最有只有一個元素
[11,2,3,43] [23,5,6,9,10]
[11,2] [3,43] [23,5] [6,9,10]
[11] [2] [3] [43] [23] [5] [6] [9,10]
[11] [2] [3] [43] [23] [5] [6] [9] [10]
------------------------------------------------
合并
[2,11] [3,43] [5,23] [6,9]
[2,3,11,43] [5,6,9,23]
[2,3,5,6,9,11,23,43]

3、代碼1：合并兩個有序數組

def mergerArr(arr_a,arr_b):
    """這個是合并2個有序數組的合并算法"""
    result = []
    idx_a =0
    idx_b =0
    #idx_a和idx_b分別執行數組a和數組b的第一個元素，一次比較兩個指針指向的元素值，取較小元素放入result,然后挪動指針進行比較
    while idx_a<len(arr_a) and idx_b<len(arr_b):
        if arr_a[idx_a]<=arr_b[idx_b]:
            result.append(arr_a[idx_a])
            idx_a+=1
        elif arr_a[idx_a]>arr_b[idx_b]:
            result.append(arr_b[idx_b])
            idx_b+=1
    #比較結束完了以后，其中一個數組已經取完值了，另外一個數組還沒有
    print("idx_a = %s idx_b = %s"%(idx_a,idx_b))
    if idx_a==len(arr_a):
        result.extend(arr_b[idx_b:])
    else:
        result.extend(arr_a[idx_a:])
    return result
arr_b = [1,4,5,6]
arr_a = [4,4,8,10]
print(mergerArr(arr_a,arr_b))
#結果
idx_a = 2 idx_b = 4
[1, 4, 4, 4, 5, 6, 8, 10]

4、代碼2：無序數組拆分過程

def mergeSort(arr):
    if len(arr)<=1:
        return arr
    mid = len(arr)//2
    left = mergeSort(arr[:mid])
    right = mergeSort(arr[mid:])
    print("left=%s\nright=%s"%(left,right))
        #拆分后，到只剩下一個元素了mid和left才返回值了，才能做合并的過程
    return mergerArr(left,right)
    
arr = [11,2,3,43,23,5,6,9]
print(mergeSort(arr))

5、最終代碼

def mergerArr(arr_a,arr_b):
    """這個是合并2個有序數組的合并算法"""
    result = []
    idx_a =0
    idx_b =0
    #idx_a和idx_b分別執行數組a和數組b的第一個元素，一次比較兩個指針指向的元素值，取較小元素放入result,然后挪動指針進行比較
    while idx_a<len(arr_a) and idx_b<len(arr_b):
        if arr_a[idx_a]<=arr_b[idx_b]:
            result.append(arr_a[idx_a])
            idx_a+=1
        elif arr_a[idx_a]>arr_b[idx_b]:
            result.append(arr_b[idx_b])
            idx_b+=1
    #比較結束完了以后，其中一個數組已經取完值了，另外一個數組還沒有
    print("idx_a = %s idx_b = %s"%(idx_a,idx_b))
    if idx_a==len(arr_a):
        result.extend(arr_b[idx_b:])
    else:
        result.extend(arr_a[idx_a:])
    return result

def mergeSort(arr):
    if len(arr)<=1:
        return arr
    mid = len(arr)//2
    left = mergeSort(arr[:mid])
    right = mergeSort(arr[mid:])
    print("left=%s\nright=%s"%(left,right))
    #拆分后，到只剩下一個元素了mid和left才返回值了，才能做合并的過程
    return mergerArr(left,right)
    
arr = [11,2,3,43,23,5,6,9]
print(mergeSort(arr))

結果：

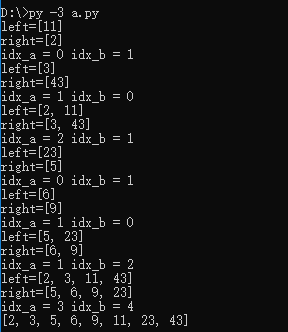
6、時間復雜度

由于遞歸拆分的時間復雜度是logN

然而，進行兩個有序數組排序的方法復雜度是N

該算法的時間復雜度是N*logN

所以是O(NlogN)

7、快速排序和歸并排序

歸并和快排都是用到遞歸的處理方式。

歸并排序的處理過程是由下到上的，先解決子問題然后再合并的；

快排和歸并正好相反，快排的處理是由上到下的,是先分區然后再去處理子問題。

歸并是穩定排序，快排不是穩定排序；

特殊情況歸并的性能比快排稍微好一點。

posted @ 2020-12-07 17:33 hqq的進階日記閱讀(330) 評論(0) 收藏舉報

刷新頁面返回頂部

算法學習：歸并排序

公告