賽時 AC ABCD，賽后補出了 E。
由于比賽在一個月前，本來已經忘記這場比賽了，直到我看到了：

（來自一位超厲害的小學同學神犇）
\(364\)？很近的比賽啊，我打過嗎？似乎打過？
打開題目一看：這不就是斯坦納樹板題嗎？但我為什么沒印象？
打開 AT 一看，額，我還真打過：

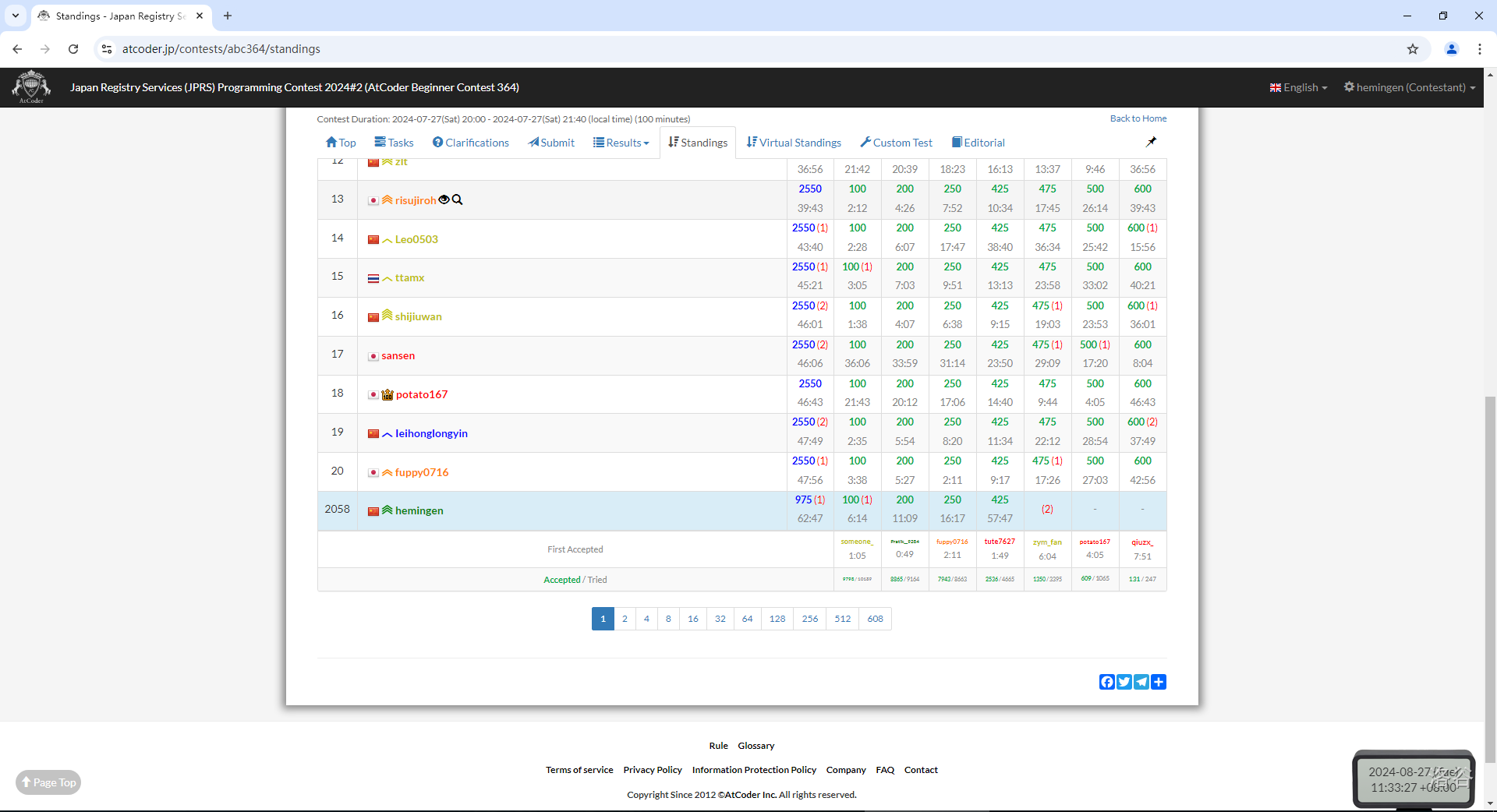
菜爆了。。。也難怪對 G 沒印象。
重新看一下題，發現還挺好玩，遂把 F、G 題干掉了。

作為第二場 AK 的比賽（第一場是 ABC126，但是太簡單了），決定寫篇總結。

以下 \(5\) 題是比賽當天做的。

[ABC364A] Glutton Takahashi

只要判斷是否有 \(2\) 個連續的 sweet。
笑點解析：賽時吃了一發罰時，數組下標寫錯了。
過此題時比賽已經過去了 \(6\) 分鐘。

[ABC364B] Grid Walk

按題意模擬。
過此題時比賽已經過去了 \(11\) 分鐘。

[ABC364C] Minimum Glutton

貪心。
想要停止吃飯，甜度限制和咸度限制只需要超過一個就可以了。所以可以分別按甜度和咸度從大到小排序，看哪種策略先結束。
過此題時比賽已經過去了 \(16\) 分鐘。

[ABC364D] K-th Nearest

二分套二分，需要思維轉換。
與直接其求距離給定點第 \(k\) 近的點是哪個，不如直接求這個距離。設給定點坐標為 \(x\)，二分這個距離（記為 \(b\)），看在 \([x-b,x+b]\) 的范圍內有幾個點。區間查詢使用線段樹，由于值域范圍過大，動態開點。
然而剛才看題解區發現全是二分套二分……二分距離后，二分距離 \(x-b,x+b\) 最近的點，判斷中間的點的數量。
賽后為了漲咕值寫了篇題解。
過此題時比賽已經過去了 \(57\) 分鐘。

[ABC364E] Maximum Glutton

注意看這個 Maximum，和前文的 minimum 形成了鮮明的對比，設置懸念，吸引讀者的閱讀興趣，引發讀者的思考，前后呼應，提示我們二者有相同也有不同。
由于要吃盡量多的東西，就要求兩個參數都不能超過限制，此時一道菜的兩個參數都會對當前情況的優劣產生影響，所以貪心會比較難繃。
于是使用 DP。
然后一看數據范圍：

空間去掉 \(n\) 那維還勉強是 \(x \times y=10^8\) 剛剛好，時間就這 \(O(nxy)=8 \times 10^9\)，根本不帶超時的好吧！
賽時吃了 \(2\) 發罰時（未 AC），win！

賽后 \(20\) min 看題解。

Instead, noticing that the value of \(N\) is fairly smaller than those of \(X\) and \(Y\) in this problem, we take the following typical approach:
Swapping the key and value of DP.
Specifically, bring the number of dishes to the key and total saltiness to the value to define:

• \(dp_{i,j,k}=\) (the minimum total saltiness when choosing exactly \(k\) dishes from dishes
  \(1,2,\dots,i\) so that the total sweetness is exactly
  \(j\)).

This way, the DP table can be filled in a total of \(O(N ^2X)\) time.
All that left is to find the maximum \(k\) such that there exists \(j\) with \(dp_{N,j,k}\le Y\).

沃德？？？那么妙又那么帥的嗎？我居然沒想到，是自己太菜了……還不是因為自己不夠努力。。。
常用 DP trick \(+1\)。
于是開始補題。一開始填表法過不去，用了刷表法才過。
此時已經 \(22:18\) 了。

以下 \(2\) 題是 \(2024.8.27\) 才做的。

[ABC364F]Range Connect MST

好玩，kruskal 與并查集小技巧 \(+1\)。
按照 kruskal 的步驟去做，但是發現不能暴力判斷一條邊的兩個點是否連通。但由于一個區間的所有點都連向一個點，所以 \([l_i,r_i]\) 有幾個連通塊就會連幾條邊。暴力處理每個連通塊，把前面的合并到后面。
哦，想起來了，賽時看過幾眼。

[ABC364G]Last Major City

一眼得斯坦納樹。
先考慮只有 \(k-1\) 個關鍵點，直接復制板題代碼即可。對于每一個詢問，輸出 \(f_{i,S}\) 即可，因為當第 \(i\) 個點被連通時，可以把它當做又一個關鍵點。

總結

好比賽，好題。
希望可以多出點這樣的比賽，不要像某些比賽只會出三維前綴和。