算法
解題方案的準確而完整的描述

基本特征
可行性:能解決問題
確定性:每個步驟必須是明確定義的,不許模棱兩可,也不許有多義性
有窮性:算法必須在有限時間內做完,在執行有限個步驟后終止
擁有足夠的情報:要有一定的輸入數據,必須 有輸出結果
基本要素
對數據對象的運算和操作:算術運算(+-*÷)邏輯運算 關系運算(大小)數據傳輸(a=b)
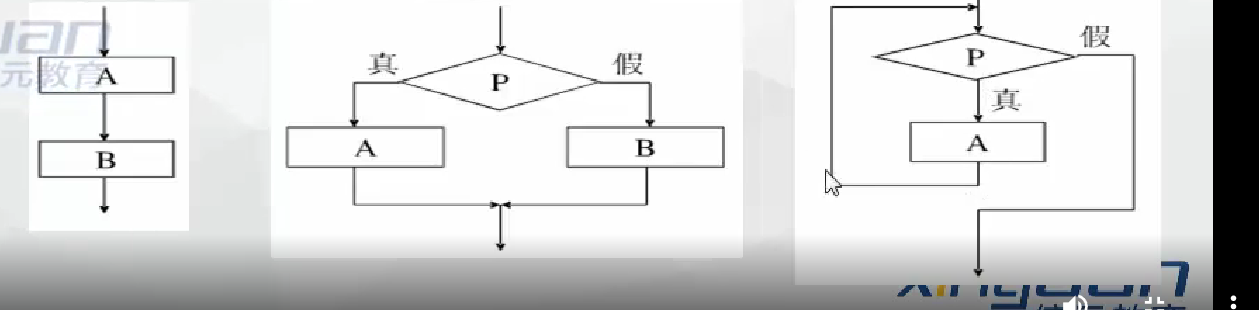
算法的控制結構:順序 選擇 循環
分析算法
常用時間復雜度和空間復雜度表示
目的:降低兩個度,提高執行效率
時間復雜度
可以用算法所執行的基本運算次數度量。與問題和問題的規模有關(兩個杯子 三個杯子
例 交換兩個杯子中的水,基本運算次數是3
分析算法工作量的方法:

空間復雜度
執行算法所需要的內存空間。包括算法程序 輸入的初始數據 執行過程中需要的額外空間(杯子c
數據結構
相互有關聯的數據元素的集合
邏輯結構
包含兩個要素

線性結構
線性表,棧,隊列

條件
有且只有一個根結點,它無前件
有且只有一個終端(葉子)結點,它無后件
除根結點和葉子結點外,其它結點有且只有一個前件,也有且只有一個后件
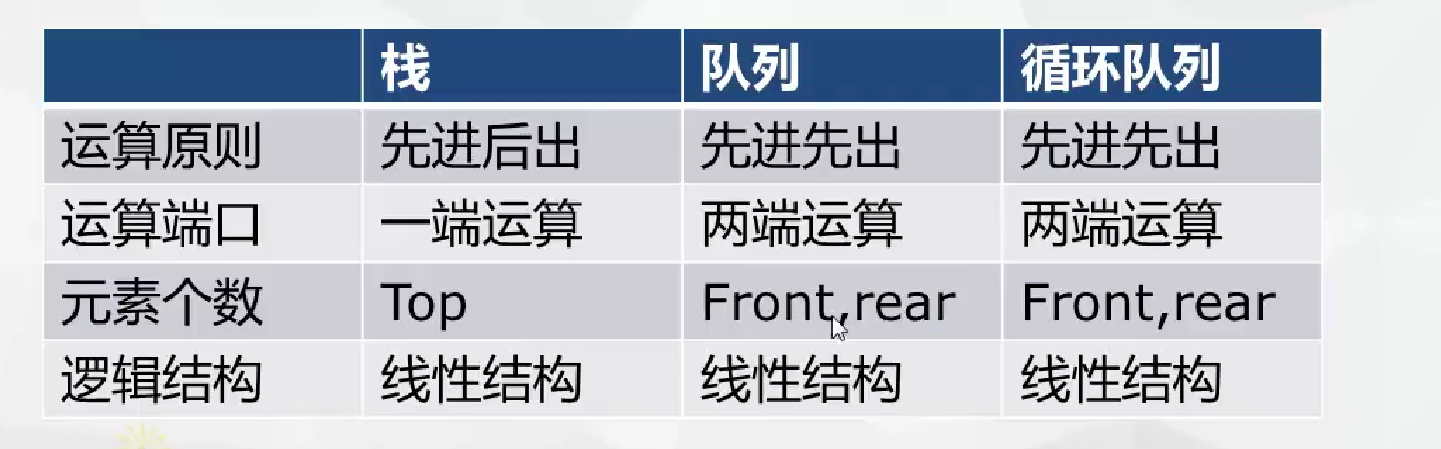
棧
限定在一端進行插入和刪除的線性表。原則是先進后出 或后進先出。具有記憶功能

棧運算

隊列
是指允許在一端進行插入,而在另一端進行刪除的線性表。原則是先進先出 或后進后出

- 循環隊列
將隊列存儲空間的最后一個位置繞道第一個位置,形成邏輯上的環狀空間
![]()
比較
非線性結構
樹

樹是n(n>0)個元素的有限集合。它有且僅有一個稱為根的元素;其余元素是互不相交的子樹
父結點:每個結點只有一個前件,為父結點
根結點:沒有前件的結點(只有一個)
子節點:每個結點的后件可以有多個,稱為子節點
葉子節點:沒有后件的結點
結點的度:一個結點所擁有的后件的個數
樹的度:所有結點中最大的度稱為樹的度
樹的深度:樹的最大層次
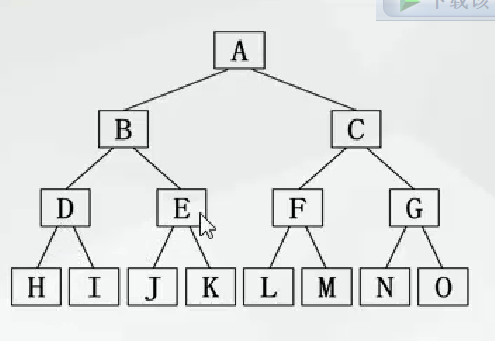
二叉樹
非空二叉樹只有一個根結點,每個結點最多有兩棵子樹(度最大是2)分別稱為左子樹和右子樹

- 滿二叉樹
每一層上的結點數均達到最大值
![]()
- 完全二叉樹
只缺少最后一層右邊的若干結點
編號為k的結點左子結點為2k,右子結點為2k+1
編號為k的結點的父結點變好為k/2
![]()
- 二叉樹的遍歷
從某一個結點出發,依次訪問到二叉樹的所有結點
前序遍歷:訪問根結點 前序遍歷左子樹 前序遍歷右子樹
中序遍歷:中序遍歷左子樹 訪問根結點 中序遍歷右子樹
8 4 9 2 10 5 1 6 3 7
后序遍歷:后序遍歷左子樹 后序遍歷右子樹 訪問根結點
8 9 4 10 5 2 6 7 3 1
存儲結構
指數據的邏輯結構在計算機存儲空間中的存放形式。一種數據結構的邏輯結構根據需要可以表示成多種存儲結構。不同的存儲結構,數據處理的效率是不同的
順序存儲

空間是連續的
順序表
線性表的順序存儲
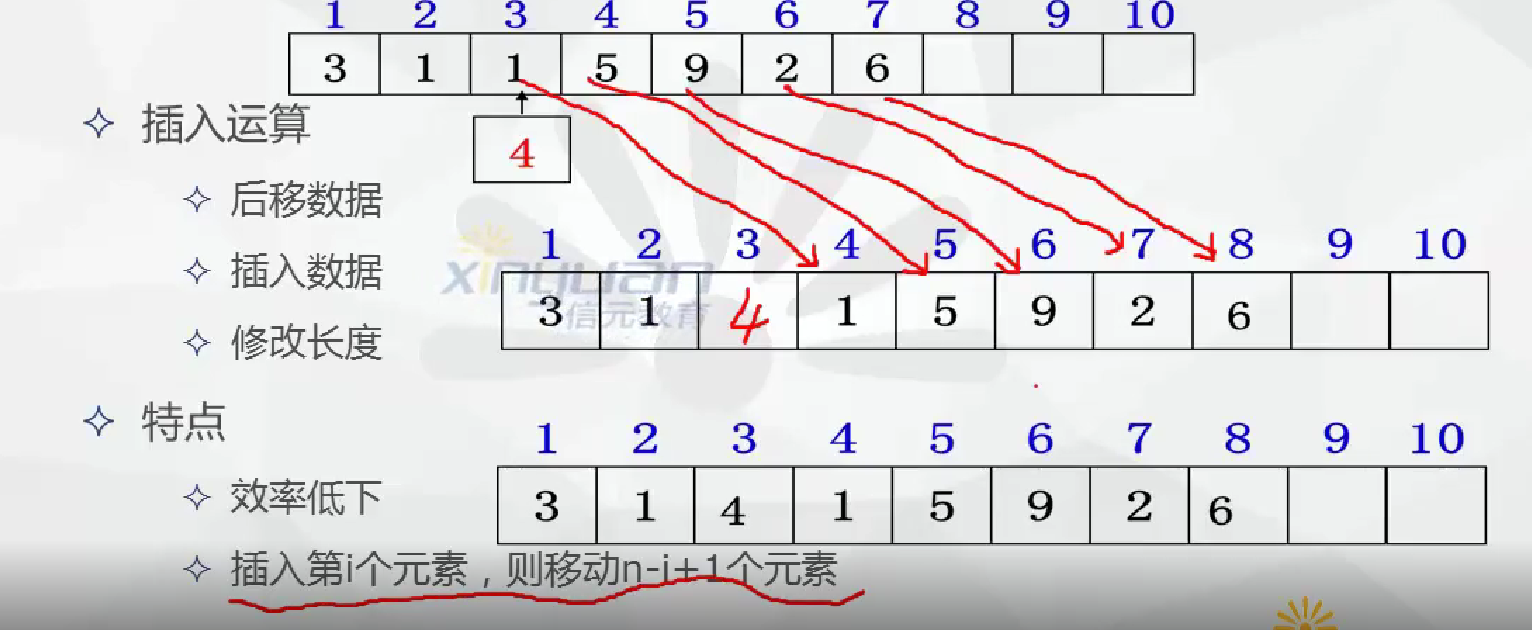
- 插入運算
![]()
- 刪除運算
![]()
鏈式(接)存儲
不需要連續的存儲空間,但需要額外的空間放小紙條

線性鏈表
線性表的鏈式存儲結構
- 單鏈表
![]()
- 帶頭結點的單鏈表
空間換時間 - 循環鏈表
![]()
- 雙向鏈表
![]()
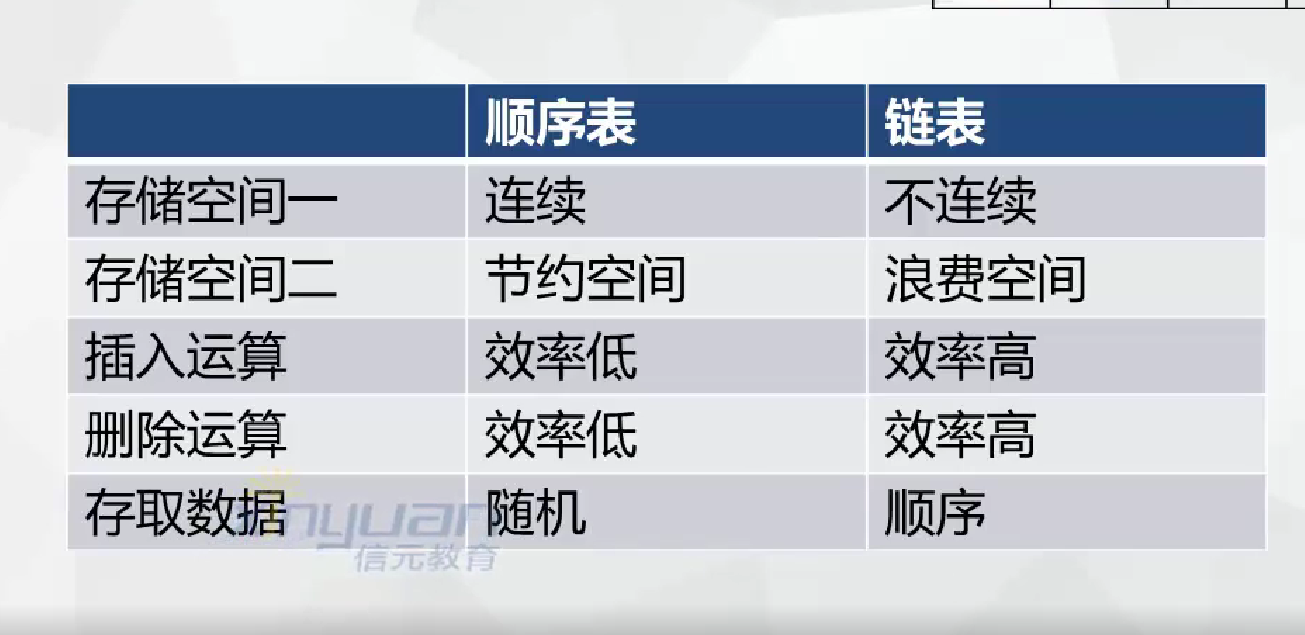
- 比較
![]()
運算
插入
刪除
查找
順序查找
適用于無序表或鏈式線性表。在最壞情況下進行n次比較
二分(對分)查找
數據必須是排好序的
即使是有序線性表,如果采用鏈式存儲結構,也只能用順序查找

排序
交換類排序法
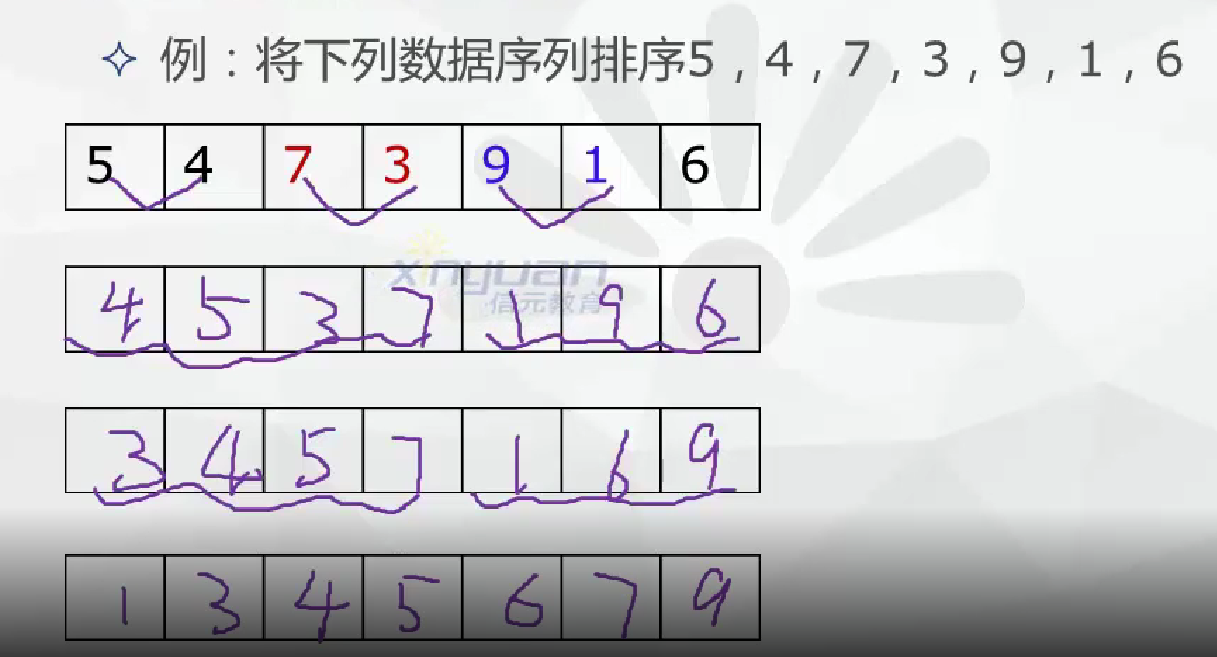
- 冒泡排序法
借助數據元素之間的互相交換進行排序的一種方法
![]()
- 快速排序
選擇一個元素T,將小于T的元素移動到T前面,將大于T的元素移動到T的后面
![]()
插入類排序法
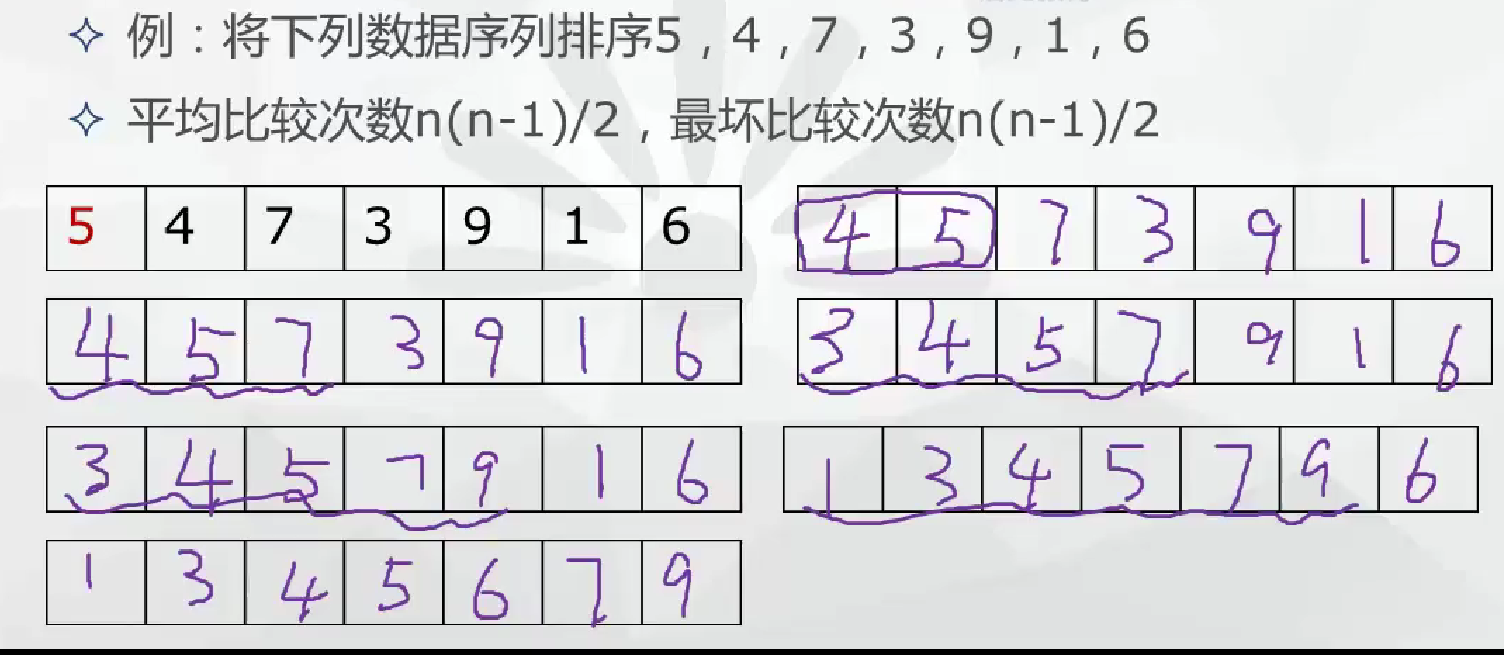
- 簡單插入排序法
將無序列表中的各元素依次插入到已經有序的線性表中
![]()
- 希爾排序法
![]()
選擇類排序法
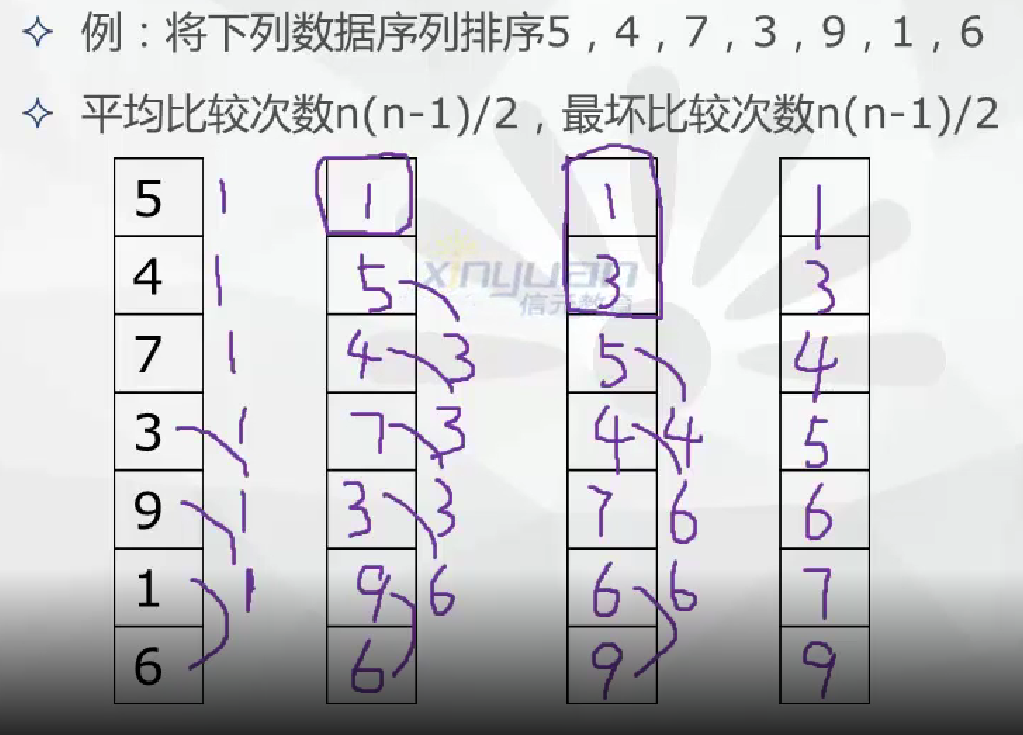
- 簡單選擇排序法
掃描整個表,從表中選一個最小的放到表的前面,剩下的表采用同樣的方法,直到子表為空為止
![]()
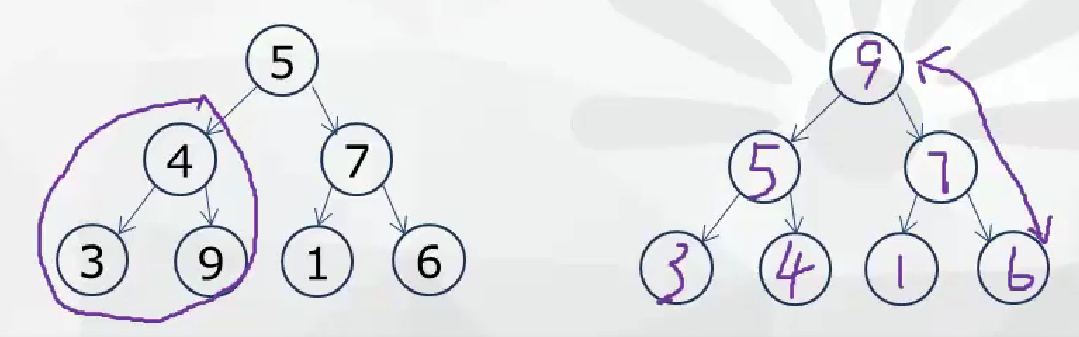
- 堆排序法
最大堆要求節點的元素都要大于其孩子,最小堆要求節點元素都小于其左右孩子,兩者對左右孩子的大小關系不做任何要求
保存時從最底下開始從右到左進行交換
![]()
![]()
![]()
歸并排序
將兩個或兩個以上的有序表組合成一個新的有序表,所需內存最大
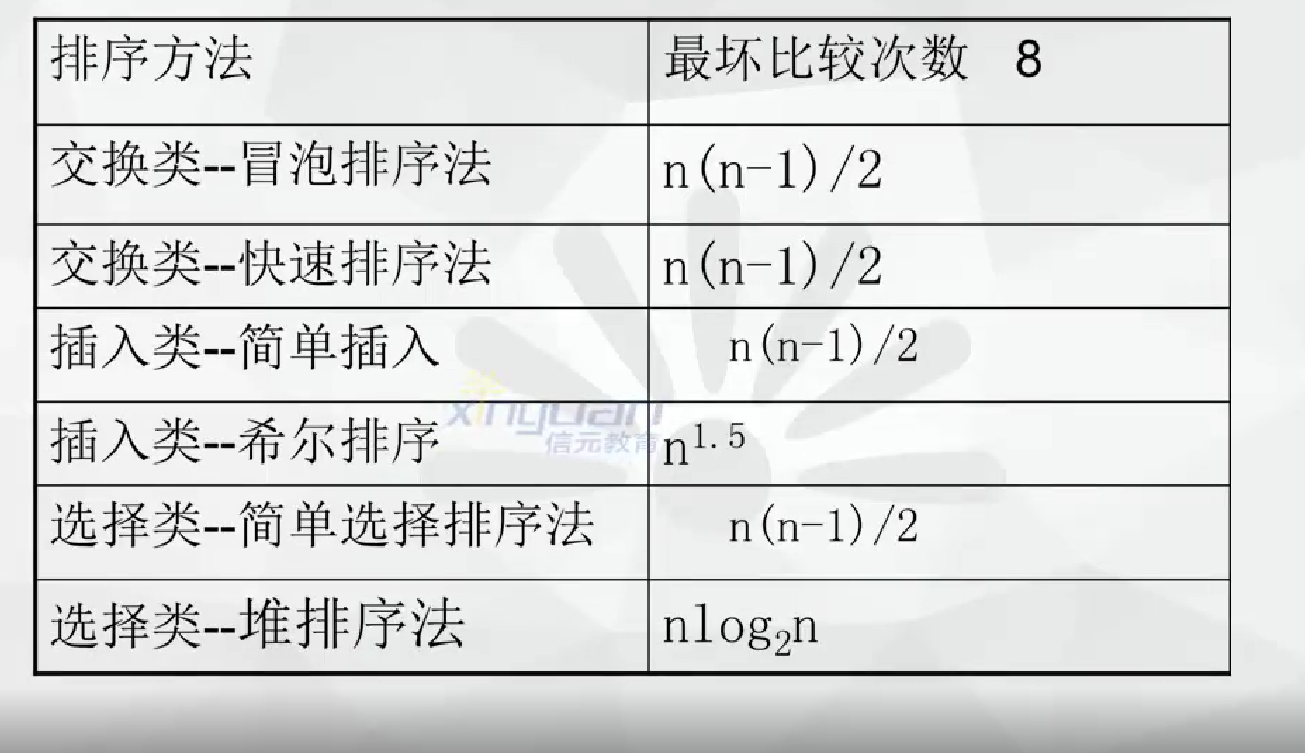
比較
求極值
對于長度為n的線性表,要比較n-1次











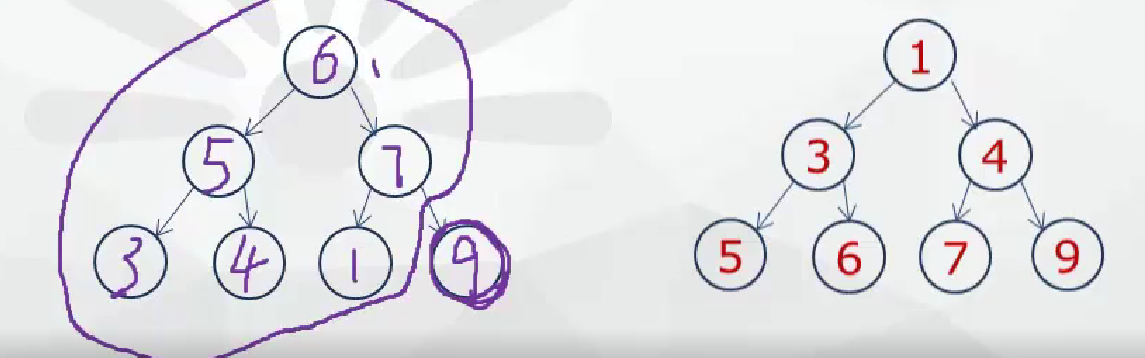

 浙公網安備 33010602011771號
浙公網安備 33010602011771號