題解_P1525 [NOIP2010 提高組] 關押罪犯
[NOIP2010 提高組] 關押罪犯
題目背景
NOIP2010 提高組 T3
題目描述
S 城現有兩座監獄,一共關押著 \(N\) 名罪犯,編號分別為 \(1\sim N\)。他們之間的關系自然也極不和諧。很多罪犯之間甚至積怨已久,如果客觀條件具備則隨時可能爆發沖突。我們用“怨氣值”(一個正整數值)來表示某兩名罪犯之間的仇恨程度,怨氣值越大,則這兩名罪犯之間的積怨越多。如果兩名怨氣值為 \(c\) 的罪犯被關押在同一監獄,他們倆之間會發生摩擦,并造成影響力為 \(c\) 的沖突事件。
每年年末,警察局會將本年內監獄中的所有沖突事件按影響力從大到小排成一個列表,然后上報到 S 城 Z 市長那里。公務繁忙的 Z 市長只會去看列表中的第一個事件的影響力,如果影響很壞,他就會考慮撤換警察局長。
在詳細考察了 \(N\) 名罪犯間的矛盾關系后,警察局長覺得壓力巨大。他準備將罪犯們在兩座監獄內重新分配,以求產生的沖突事件影響力都較小,從而保住自己的烏紗帽。假設只要處于同一監獄內的某兩個罪犯間有仇恨,那么他們一定會在每年的某個時候發生摩擦。
那么,應如何分配罪犯,才能使 Z 市長看到的那個沖突事件的影響力最小?這個最小值是多少?
輸入格式
每行中兩個數之間用一個空格隔開。第一行為兩個正整數 \(N,M\),分別表示罪犯的數目以及存在仇恨的罪犯對數。接下來的 \(M\) 行每行為三個正整數 \(a_j,b_j,c_j\),表示 \(a_j\) 號和 \(b_j\) 號罪犯之間存在仇恨,其怨氣值為 \(c_j\)。數據保證 \(1<a_j\leq b_j\leq N, 0 < c_j\leq 10^9\),且每對罪犯組合只出現一次。
輸出格式
共一行,為 Z 市長看到的那個沖突事件的影響力。如果本年內監獄中未發生任何沖突事件,請輸出 0。
樣例 #1
樣例輸入 #1
4 6
1 4 2534
2 3 3512
1 2 28351
1 3 6618
2 4 1805
3 4 12884
樣例輸出 #1
3512
提示
輸入輸出樣例說明
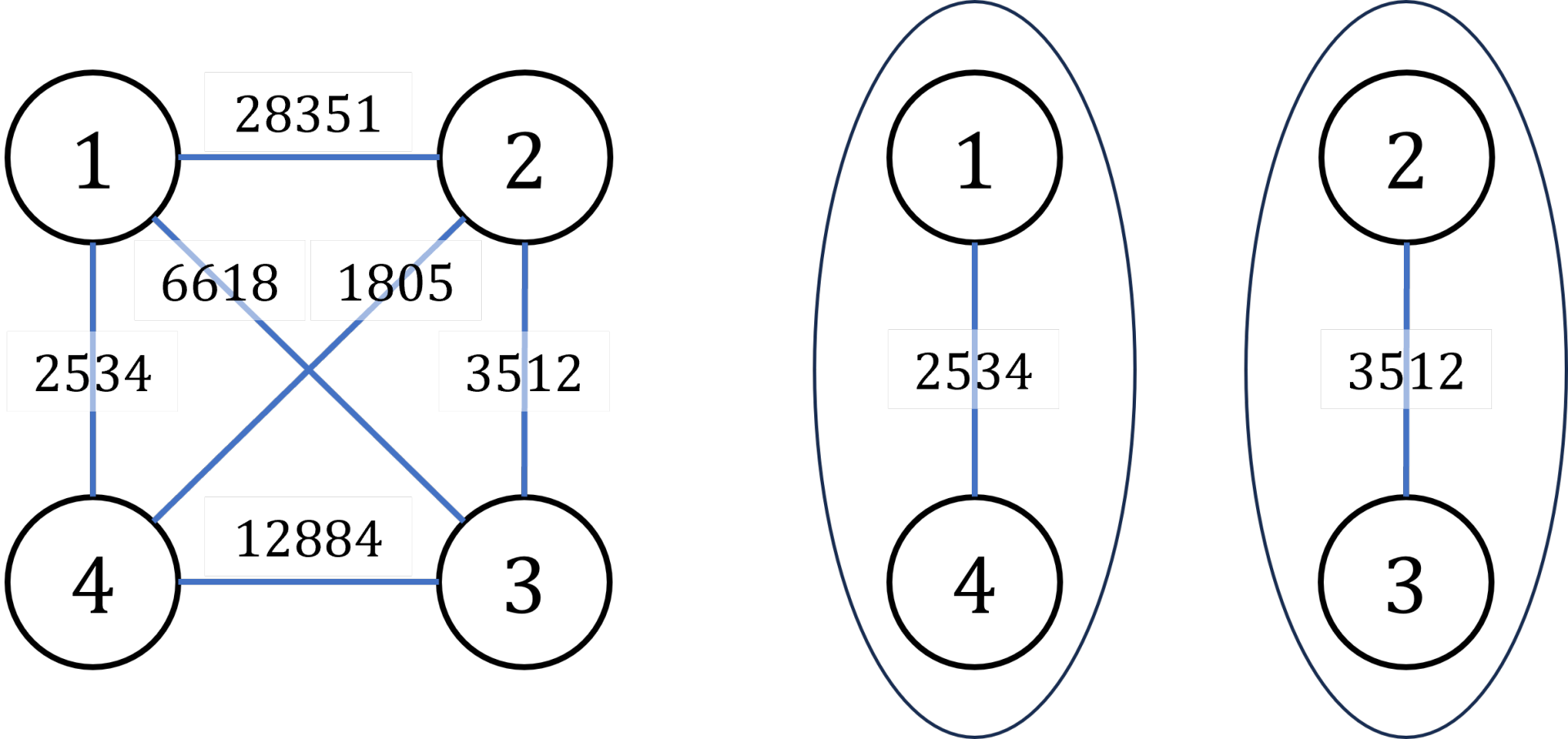
罪犯之間的怨氣值如下面左圖所示,右圖所示為罪犯的分配方法,市長看到的沖突事件影響力是 \(3512\)(由 \(2\) 號和 \(3\) 號罪犯引發)。其他任何分法都不會比這個分法更優。
數據范圍
對于 \(30\%\) 的數據有 \(N\leq 15\)。
對于 \(70\%\) 的數據有 \(N\leq 2000,M\leq 50000\)。
對于 \(100\%\) 的數據有 \(N\leq 20000,M\leq 100000\)。
題解
思路分析
【方法1】二分答案+染色二分圖
題目中有明顯的求最大值最小的概念,于是可以考慮二分答案,對于最大值檢查可以采用二分圖染色。
【方法2】貪心+并查集(帶權/擴展域名)
由于題目的答案一定是其中的某一條邊長,怎么使得該邊長最小?
可以想到每次先將較大值放入不同監獄,如果可以放置,那么后面的答案一定更小;如果不能放置,則其就是答案。
所以可以按照邊長排序,降序合并每條邊即可。
合并的時候有兩種策略
- 帶權并查集:使用權值來維護當前元素與根節點元素的種類關系,如 d[u]=0表示 u與root是同類,d[u]=1表示不同類。帶權并查集的find和union操作需要適當更新權值數組d[u];
int find(int u) {
if (u != p[u]) {
int fu = p[u];
p[u] = find(p[u]);
d[u] = (d[u] + d[fu]) % 2;
}
return p[u];
}
void union_(int u, int v) {
int a = find(u), b = find(v);
p[a] = b;
d[a] = ((d[v] - d[u] + 2) % 2 + 1) % 2;
}
- 擴展域并查集:將并查集的規模擴展為原來的兩倍,前一半用于維護朋友關系,后一半用于維護敵人關系。如 (u,u+n) 是敵人,(v,v+n) 是敵人,當 (u,v)是敵人的時候,根據敵人的敵人是朋友,可以將 u 與 u的敵人(v)的敵人(v+n)合并,即合并 (u, v+n);同理合并 (v, u+n)。
程序實現
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e4 + 10, M = 1e5 + 10, INF = 0x3f3f3f3f;
int n, m, p[N << 1], d[N << 1];
struct T {
int u, v, w;
bool operator<(const T& t) const { return w < t.w; }
} g[M];
// -------------------
// 二分答案+染色二分圖
vector<int> G[N];
int color[N], flag;
void dfs(int u, int c) {
color[u] = c;
for (auto v : G[u]) {
if (!color[v]) dfs(v, ~c);
else if (color[v] == c) flag = 0;
}
}
bool chk(int k) { // 將邊權 >k 的建圖,檢查是否可以進行二分圖染色
for (int i = 1; i <= n; i++) G[i].clear();
for (int i = k + 1; i <= m; i++) {
int u = g[i].u, v = g[i].v;
G[u].push_back(v), G[v].push_back(u);
}
flag = 1, memset(color, 0x00, sizeof color);
for (int i = 1; i <= n && flag; i++)
if (!color[i]) dfs(i, 1);
return flag;
}
int solve1() {
int l = 0, r = m, ans = 0;
while (l <= r) {
int mid = l + r >> 1;
chk(mid) ? r = mid - 1, ans = mid : l = mid + 1;
}
return g[ans].w;
}
// -------------------
int find(int u) {
if (u != p[u]) {
int fu = p[u];
p[u] = find(p[u]);
d[u] = (d[u] + d[fu]) % 2;
}
return p[u];
}
// 帶權并查集
// d[i]表示 i與根節點的關系:0-朋友,1-敵人
int solve2() {
for (int i = 0; i <= n; i++)
p[i] = i, d[i] = 0;
for (int i = m; i >= 1; i--) {
int u = g[i].u, v = g[i].v;
int a = find(u), b = find(v);
if (a == b && (d[u] - d[v] + 4) % 2 == 0)
return g[i].w;
p[a] = b;
d[a] = ((d[v] - d[u] + 2) % 2 + 1) % 2;
}
return 0;
}
// 擴展域并查集
// 敵人的敵人是朋友:u,u+n是敵人,u,v是敵人,將u放入v的敵人v+n的集合
int solve3() {
for (int i = 0; i <= n * 2; i++)
p[i] = i;
for (int i = m; i >= 1; i--) {
int u = g[i].u, v = g[i].v;
int a = find(u), b = find(v);
if (a == b)
return g[i].w;
p[a] = find(v + n);
p[b] = find(u + n);
}
return 0;
}
int main() {
cin >> n >> m;
for (int i = 1, u, v, w; i <= m; i++)
cin >> u >> v >> w, g[i] = {u, v, w};
sort(g + 1, g + 1 + m);
// cout << solve1() << endl;//AC
// cout << solve2() << endl;//AC
cout << solve3() << endl; // AC
return 0;
}
/*
P1525 [NOIP2010 提高組] 關押罪犯
https://www.luogu.com.cn/problem/P1525
in:
4 6
1 4 2534
2 3 3512
1 2 28351
1 3 6618
2 4 1805
3 4 12884
out:3512
*/



 浙公網安備 33010602011771號
浙公網安備 33010602011771號