1.11 循環結構實例

1. 小魚游泳

【例】有一只小魚，它平日每天游泳 50 公里，周末休息（實行雙休日)，假設從周 x(1≤x≤7) 開始算起，過了 n(n≤1e6)天以后，小魚一共累計游泳了多少公里呢？

輸入格式：輸入兩個整數x,n(表示從周x算起，經過n天）。

輸出格式：輸出一個整數，表示小魚累計游泳了多少公里。

輸入樣例：3 10
輸出樣例：400

#include<iostream>
using namespace std;

int main(){
    int x,n, ans=0; cin>>x>>n;
    for(int i=1; i<=n; i++, x++){
        if(x>7) x%=7;//如果是周八，那就回到周一
        if(x>=1 && x<=5) ans+=50;
    }
    cout<<ans;
    return 0;
} 

2. 棋盤

【例】輸入三個自然數 n, i, j （1<=i, j<=N），輸出在一個NxN格的棋盤中，與格子（i，j）同行、同列、同一對角線的所有格子的位置。
例如：n=4, i=2, j=3，表示在4x4棋盤中，指定位置為第2列第3行

輸入樣例：4 2 3
輸出樣例：
(2,1) (2,2) (2,3) (2,4)   //{同一行上格子的位置}
(1,3) (2,3) (3,3) (4,3)   //{同列列上格子的位置}
(1,2) (2,3) (3,4)         //{左上到右下對角線上的格子的位置}
(4,1) (3,2) (2,3) (1,4)   //{左下到右上對角線上的格子的位置}

解析：這樣的題目一旦涉及到二維地圖坐標，就可以考慮找下標規律，如

假設原地圖的坐標是這樣的：

11  12  13  14 
21  22  23  24
31  32  33  34
41  42  43  44

按照 ij 的形式書寫， i表示行數，j表示列數
并且根據這樣的坐標圖，可以找到規律：
同一行：i相等
同一列：j相等
左上角到右下角：j-i是定值
左下角到右上角：i+j是定值

在根據這樣的規律來解題：參考程序如下
    
#include<iostream>
using namespace std;

int main(){
    int n=4,x=2,y=3; cin>>n>>x>>y;
    for(int i=1; i<=n; i++){
        cout<<"("<<x<<","<<i<<") ";//同一行，行不變
    }cout<<endl;
    
    for(int i=1; i<=n; i++){
        cout<<"("<<i<<","<<y<<") ";//同一列，列不變
    }cout<<endl;

    for(int i=1; i<=n; i++){
        for(int j=1; j<=n; j++){//左上到右下，j-i是定值
            if(j-i==y-x) cout<<"("<<i<<","<<j<<") ";
        }
    }cout<<endl;

    for(int i=n; i>=1; i--){
        for(int j=1; j<=n; j++){//左下到右上，i+j是定值
            if(i+j==x+y) cout<<"("<<i<<","<<j<<") ";
        }
    }
    return 0;
}

3. 積木大賽

【例】春春幼兒園舉辦了一年一度的“積木大賽”。今年比賽的內容是搭建一座寬度為n的大廈,大廈可以看成由n塊寬度為1的積木組成第i塊積木的最終高度需要是hi 。
在搭建開始之前,沒有任何積木(可以看成n塊高度為0的積木)。接下來每次操作，小朋友們可以選擇一段連續區間[L,R]，然后將第L塊到第R塊之間(含第L塊和第R塊)所有積木的高度分別增加1，小M是個聰明的小朋友，她很快想出了建造大廈的最佳策略，造所需的操作次數最少。但她不是一個勤于動手的孩子，所以想請你幫忙實現這個策略，并求出最少的操作次數。

輸入格式：

輸入包含兩行，第1行包含一個整數n,表示大廈的寬度；
第2行包含n個整數,第i個整數為hi。

輸出格式：

輸出僅1行，即建造所需的最少操作數。

輸入樣例

5
2 3 4 1 2

輸出樣例：5

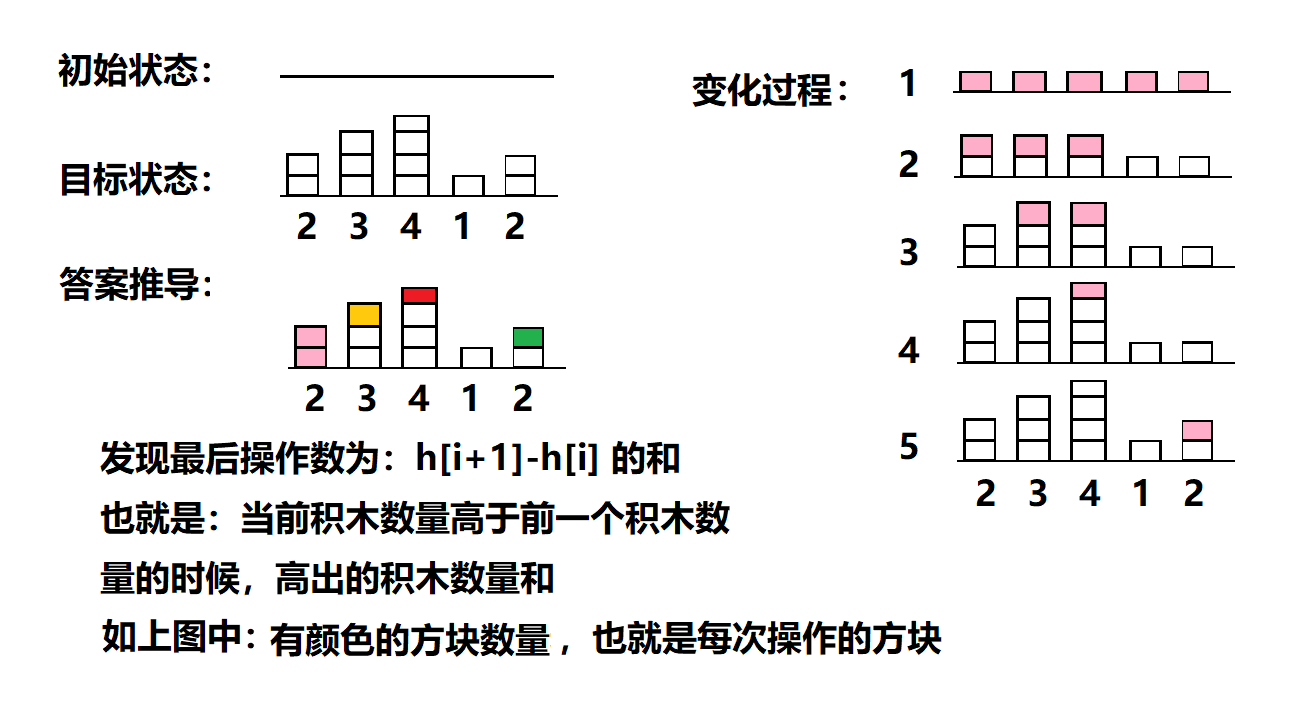
說明：其中一種可行方案[1,5] [1,3] [2,3] [3,3] [5,5]

數據范圍： 1<=n<=100000, 0<=hi<=10000

解析：這道題目需要仔細讀題，認真分析，找到問題的關鍵之處。

當 h[i+1] > h[i] 時，結果應該新增 h[i+1]-h[i]

當 h[i+1] <= h[i] 時，不用操作

#include<iostream>
using namespace std;

int main(){
    int n; cin>>n;
    int ans=0,h=0;
    for(int i=1; i<=n; i++){
        int a; cin>>a;
        if(a>h) ans += a-h;
        h=a;
    }
    cout<<ans;
    return 0;
}