柯尼斯堡七橋問題

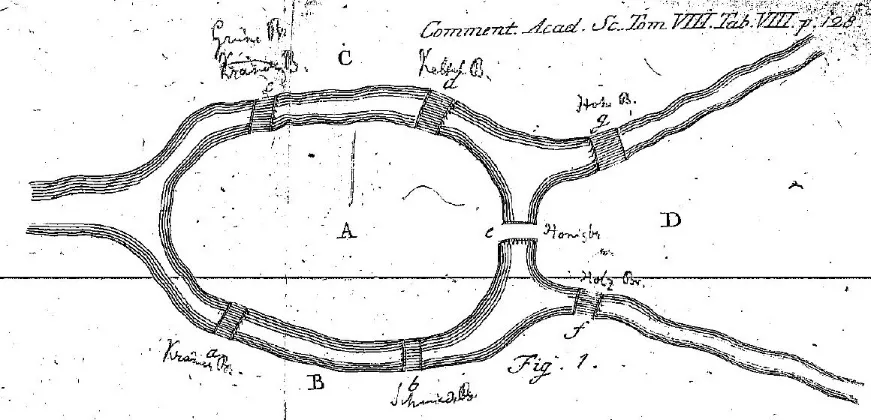
18世紀(jì)時，歐洲的一個小城柯尼斯堡有七座橋，連接了四個地方，如下圖所示。人們聊天時，有人提出這樣一個問題：是否存在一種方法，能夠從一個地點(diǎn)出發(fā)，經(jīng)過每座橋一次且僅一次，最后回到起點(diǎn)。人們討論了很長時間，都沒有找到方案。

歐拉出手

這個問題引起了歐拉的興趣。他稍微研究了以下，很快就證明了該問題是無解的。即不存在一種走法，能夠從某個地點(diǎn)出發(fā)，經(jīng)過每座橋一次且僅一次，最后回到起點(diǎn)。
歐拉是如何思考這個問題的呢？

首先，他簡化了一下。將四塊陸地看做四個點(diǎn)，將七座橋看做是七條邊，得到如下的圖：

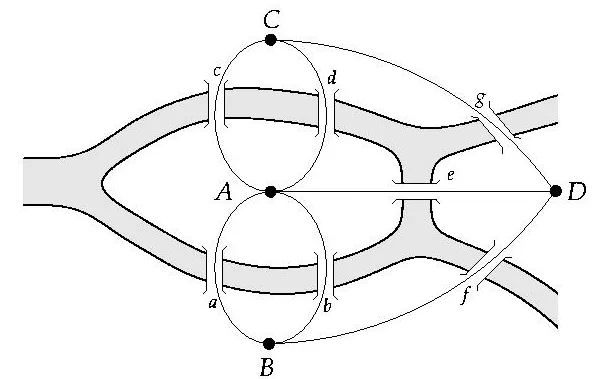
現(xiàn)在只需要在A、B、C、D四點(diǎn)中選一個點(diǎn)為起點(diǎn)，一筆畫完該圖，最后回到起點(diǎn)。

我們發(fā)現(xiàn)，如果存在這樣一條線路，那么與每個點(diǎn)相連接的邊一定是偶數(shù)條。
這很顯然，因為對于起點(diǎn)而言，一定是先出后進(jìn)，而對于其他點(diǎn)，一定是先進(jìn)后出。每條邊只能走一次。這就要求與該點(diǎn)相連的邊必須是偶數(shù)條。
而上圖不符合這個條件，所以他是無解的。

我們用度來表示一個點(diǎn)相連的邊數(shù)。如果一個點(diǎn)的度為偶數(shù)，則稱為偶點(diǎn)；否則稱為奇點(diǎn)。

歐拉不僅解決了七橋問題，還得出了一個結(jié)論，開創(chuàng)了人類對圖論的研究。

• 如果所有的點(diǎn)都是偶點(diǎn)，則該圖可以一筆畫完，并回到起點(diǎn)。
• 如果僅存在兩個奇點(diǎn)，則可以從一個奇點(diǎn)出發(fā)，一筆畫完，最終到達(dá)另一個奇點(diǎn)。
• 其他情況，圖不能一筆畫完

人們把能夠一筆畫完并回到起點(diǎn)的圖，稱為歐拉回路；把能夠一筆畫完，但不能回到起點(diǎn)的圖，稱為歐拉通路。

一筆畫問題

我們已經(jīng)知道如何判斷一個圖是不是歐拉回路或者歐拉通路。
如果是歐拉回路或者歐拉通路，如何輸出一種一筆畫完的方案呢？
這樣的方案可能有多種，我們只需要輸出任意一種即可。

可以使用dfs，走過的邊馬上刪掉, 如果一個點(diǎn)的邊都刪完了，則將該點(diǎn)加入到一個序列。dfs結(jié)束后，該序列即為一筆畫的路徑。

void dfs(int s){
    vis[s] = 1;
    for(int i = 1; i <= n; i++){
        if(arr[s][i]){
            arr[s][i] = arr[i][s] = 0;
            dfs(i);
        }
    }
    path[top++] = s;
}

這是一個簡單而神奇的算法。它有點(diǎn)類似于樹的后序序列。
但改為先序序列就不對了。這很好理解。因為來到分叉口，如果選擇一條錯誤的路，那么有些分支就永遠(yuǎn)錯過了。后面雖然遞歸返回時能夠我們重新光顧這個岔路口，但是在路徑上不是連續(xù)的。

而改成后序序列后，在任何一個分岔路口，不管選擇那一條走，后序序列都能夠保證最后回到這個岔路口。等到所有的岔路口都走了并返回后，再來時的路返回，這樣路徑就接上了。
比如有一條邊\((i,j)\),現(xiàn)在從\(i\)走到了\(j\)，那么返回時能夠保證\(j\)的所有其他岔路都走了并且返回了以后，再返回到\(i\)點(diǎn)。

例題1：

對給定的一個無向圖，判斷能否一筆畫出。若能，輸出一筆畫的先后順序，否則輸出“No Solution!”
所謂一筆畫出，即每條邊僅走一次，每個頂點(diǎn)可以多次經(jīng)過。
輸出字典序最小的一筆畫順序。

分析：首先判斷是不是一筆畫的圖？如果有0個奇點(diǎn)或者2個奇點(diǎn)，則可以一筆畫，否則直接輸出"No Solution!".

如何保證字典序最小呢？
因為我們是后序遍歷，先訪問的點(diǎn)，實(shí)際上是后進(jìn)入隊列的。所以， 我們按照編號由小到大的順序依次dfs，最后將隊列逆序輸出即可。
如果全為偶點(diǎn)，我們以\(1\)號點(diǎn)為起點(diǎn)；如果有兩個奇點(diǎn)，則從編號較小的奇點(diǎn)做dfs。

#include <bits/stdc++.h>
using namespace std;
#define maxn 105
int arr[maxn][maxn];
int n, m, top, du[maxn];
int odds, start;
bool noans;
int path[maxn * maxn];
bool vis[maxn];
int ecnt;
int visit;
void dfs(int s){
    vis[s] = 1;
    for(int i = 1; i <= n; i++){
        if(arr[s][i]){
            arr[s][i] = arr[i][s] = 0;
            dfs(i);
        }
    }
    path[top++] = s;
}
int main(){
    scanf("%d", &n);
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= n; j++){
            scanf("%d", &arr[i][j]);
            if(arr[i][j] == 1) du[i]++, ecnt++;
        }
    }
    ecnt /= 2;
    for(int i = n; i > 0; i--){
        if(du[i] % 2 == 1) {
            odds++;
            start = i;
        }
    }
    if(odds == 0){   
            dfs(1);
        }
    else if(odds == 2){
        dfs(start);
    }
    else noans = 1; 
    if(noans == 1 || top != ecnt + 1)printf("No Solution!\n");
    else {
        for(int i = top - 1; i >= 0; i--){
            printf("%d ", path[i]);
        }
    }
    return 0;
}

例題二

題目描述：

給定n個各不相同的無序字母對（區(qū)分大小寫，無序即字母對中的兩個字母可以位置顛倒）。請構(gòu)造一個有n+1個字母的字符串使得每個字母對都在這個字符串中出現(xiàn)。
如果有多種方案，請輸出前面的字母的ASCII編碼盡可能小的（字典序最小）的方案

分析

將52個字母看做52個點(diǎn)，如果出現(xiàn)一個字母對，則將對應(yīng)的兩個點(diǎn)連一條無向邊。
判斷是否是歐拉回路，輸出一筆畫的順序即可。