基于SOA海鷗優化算法的PID控制器最優控制參數計算matlab仿真
1.課題概述
基于SOA海鷗優化算法的PID控制器最優控制參數計算matlab仿真,通過SOA優化PID的kp,ki,kd三組參數,對比普通的PID控制器的控制效果。
2.系統仿真結果

3.核心程序與模型
版本:MATLAB2022a
%使用優化后的參數控制PID控制器
for k=1:10000
time(k) = k*ts;
%設定比例系數kp
kp = kps(end);
ki = kis(end);
kd = kds(end);
% 設定參考輸入 rin(k) 的值為 1,可視為階躍輸入
Ref(k) = 1;
% 計算控制輸出 u(k),使用 PID 控制器的計算方式,根據狀態變量和相應系數
Uctrl(k)= kp*x(1)+kd*x(2)+ki*x(3);
% 計算系統的輸出 yout(k),根據系統的離散差分方程,利用系統的分母和分子系數以及輸入信號的歷史值
yout(k) =-den(2)*y_1-den(3)*y_2+num(2)*u_1+num(3)*u_2;
% 計算當前時刻的誤差,為參考輸入 rin(k) 與系統輸出 yout(k) 的差值
errs(k) = Ref(k)-yout(k);
% 保存輸入信號和輸出信號的前一個時刻的值,用于下一次迭代
u_2 = u_1;
u_1 = Uctrl(k);
y_2 = y_1;
y_1 = yout(k);
x(1) = errs(k);
x(2) = (errs(k)-err1)/ts;
x(3) = x(3)+errs(k)*ts;
err1 = errs(k);
end
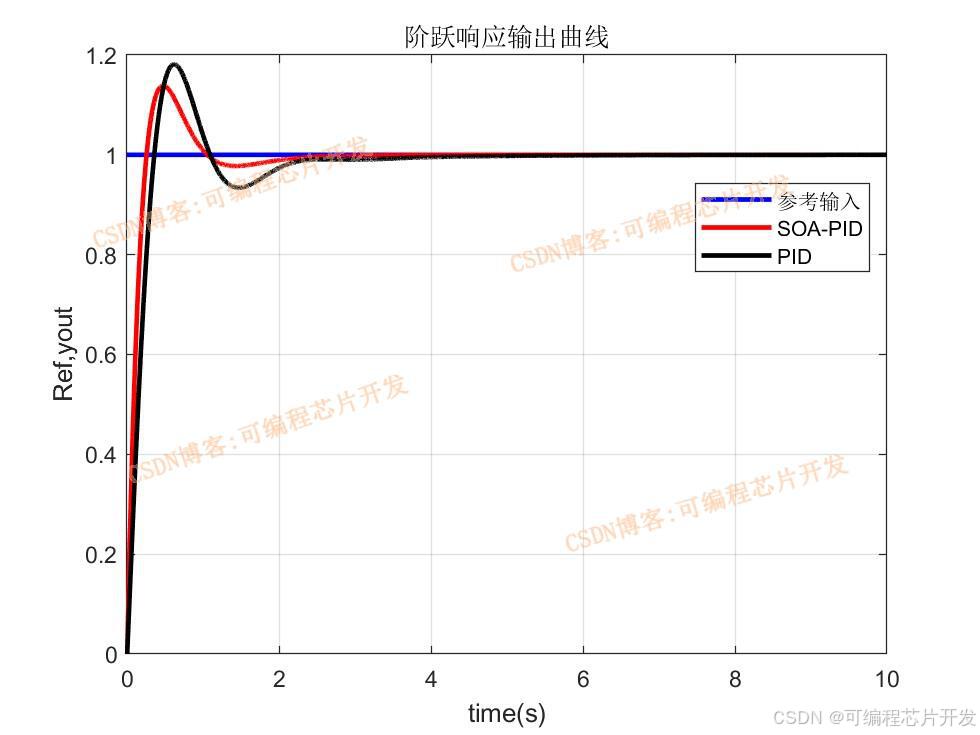
figure
plot(time,Ref,'b',time,yout,'r','LineWidth',2)
xlabel('time(s)');
ylabel('Ref,yout');
grid on
title('階躍響應輸出曲線')
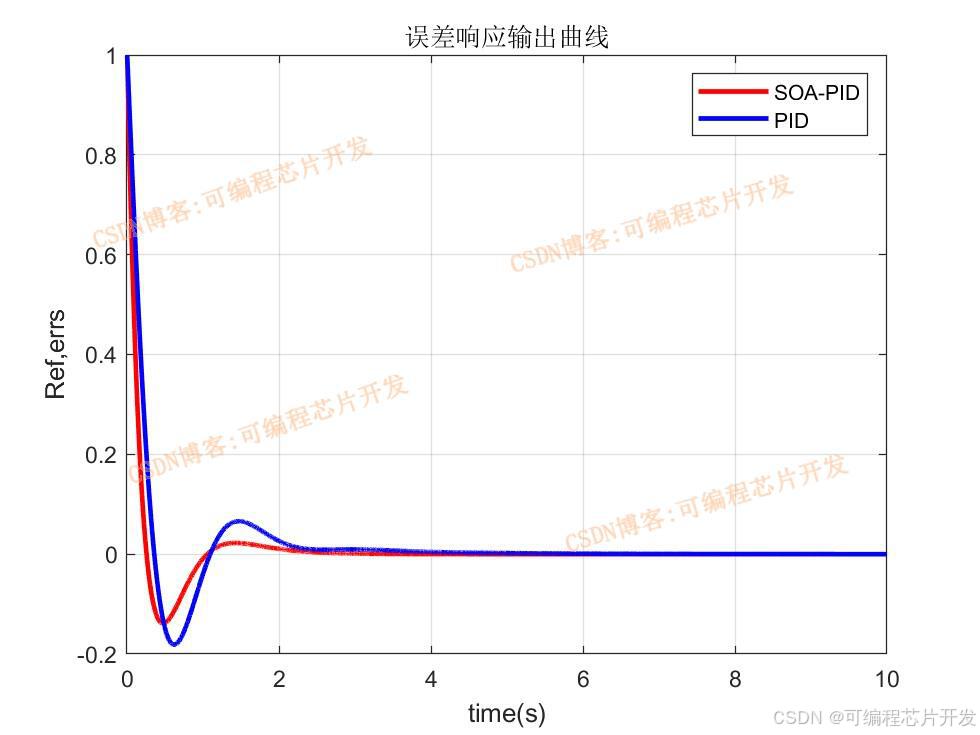
figure
plot(time,errs,'b','LineWidth',2)
xlabel('time(s)');
ylabel('Ref,errs');
grid on
title('誤差響應輸出曲線')
save R1.mat ysoas kps kis kds time errs yout Ref
4.系統原理簡介
PID(比例 - 積分 - 微分)控制器由于其結構簡單、穩定性好、可靠性高以及易于實現等優點,在工業過程控制、機器人控制、航空航天等眾多領域得到了廣泛應用。PID 控制器的性能在很大程度上取決于其三個參數(比例系數 、積分系數 、微分系數 )的取值。然而,傳統的 PID 參數整定方法,如試湊法、Ziegler-Nichols 法等,往往依賴于經驗和大量的試驗,對于復雜的控制系統,難以快速準確地找到最優的參數組合,從而影響控制系統的性能。
海鷗優化算法(SOA)是一種基于自然界海鷗群體覓食行為的新型智能優化算法。它通過模擬海鷗在搜索食物過程中的遷徙、攻擊和覓食等行為,能夠在復雜的搜索空間中有效地尋找最優解。將 SOA 應用于 PID 控制器參數的優化,可以克服傳統整定方法的不足,快速準確地確定最優的 PID 參數,提高控制系統的性能和穩定性。
在利用 SOA 優化 PID 控制器參數時,需要定義一個適應度函數來評估每一組 PID 參數(即每只海鷗的位置所代表的參數組合)的優劣。通常以控制系統的性能指標作為適應度函數,例如可以采用積分絕對誤差(IAE)、積分平方誤差(ISE)或時間乘以絕對誤差積分(ITAE)等作為適應度函數。以 IAE 為例,其計算公式為:

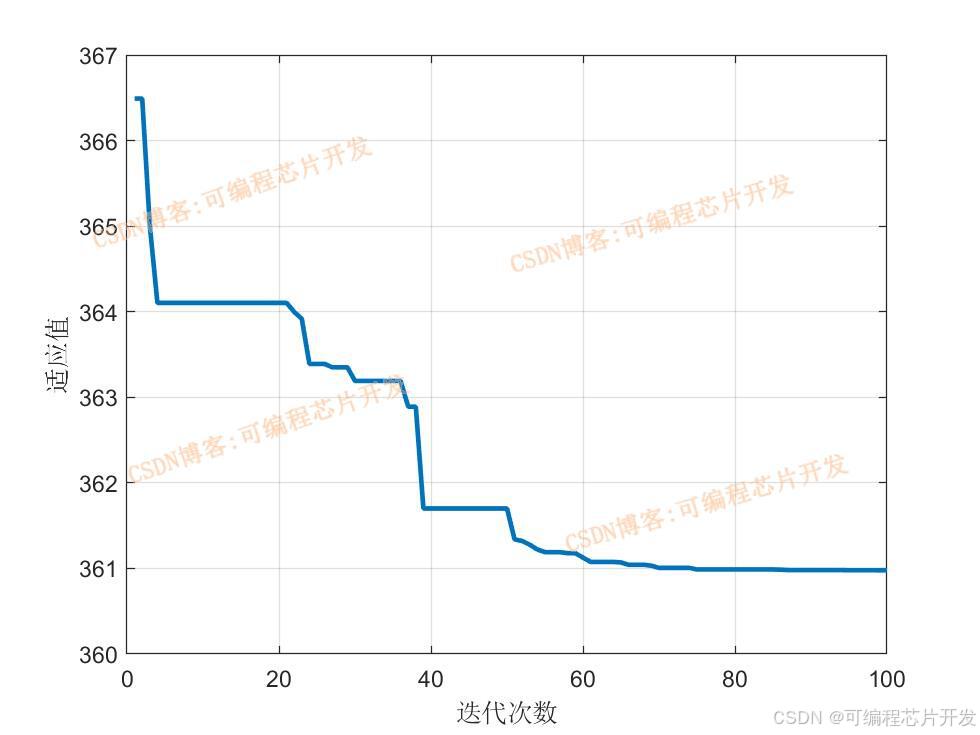
與傳統的 PID 參數整定方法相比,基于 SOA 的優化方法能夠在較短的時間內找到更接近最優解的 PID 參數組合。由于 SOA 算法通過模擬海鷗的智能行為,在全局搜索和局部搜索之間進行了有效的平衡,能夠快速地在廣闊的參數空間中定位到較優的區域,然后在該區域進行精細的搜索,從而提高了收斂速度和精度。通過大量的實驗仿真表明,在相同的控制系統和性能指標要求下,基于 SOA 的 PID 控制器參數優化方法能夠在較少的迭代次數內達到比傳統方法更低的適應度值,即更好的控制性能。



 浙公網安備 33010602011771號
浙公網安備 33010602011771號