基于空間狀態方程的車輛行駛控制系統simulink建模與仿真,對比前饋控制和PI反饋控制
1.課題概述
基于空間狀態方程的車輛行駛控制系統simulink建模與仿真,對比前饋控制和PI反饋控制。
2.系統仿真結果


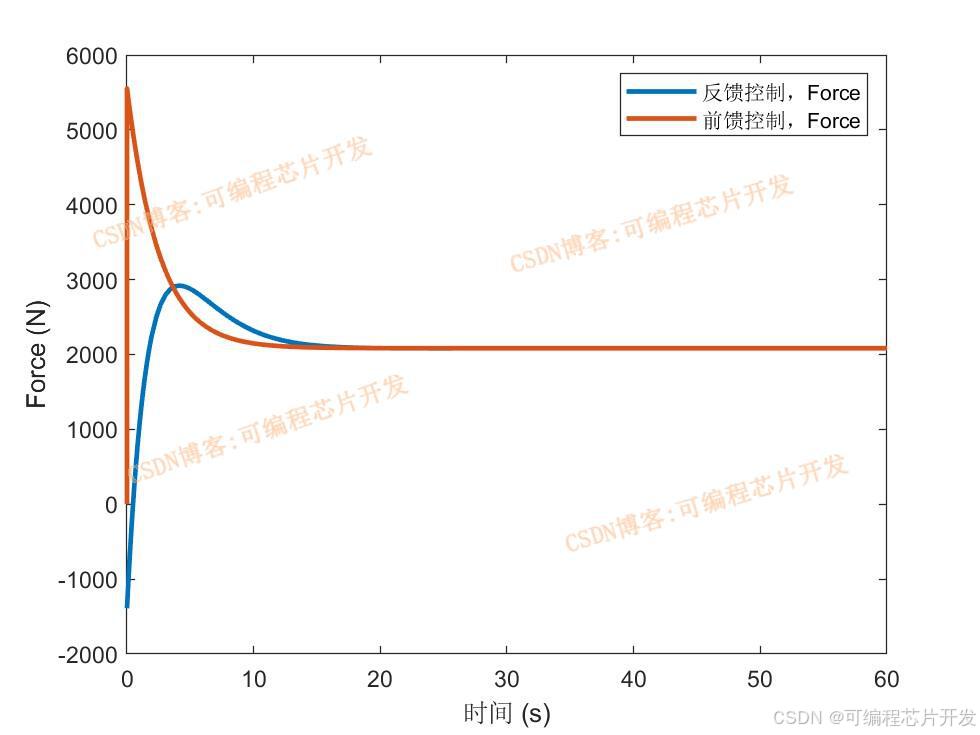
3.核心程序與模型
版本:MATLAB2022a
% 獲取輸出數據中的時間列,單位為秒
t = yout(:,1); % s, time
% 獲取輸出數據中的速度列,單位為米每秒,此處注釋中寫的's'應為筆誤,實際是速度的意思
v = yout(:,2); % s, speed (velocity)
% 獲取輸出數據中的速度誤差列,單位為米每秒
v_tilde = yout(:,3); % s, error
% 獲取輸出數據中的期望速度列,單位為米每秒
v_d = yout(:,4); % s, desired speed
% 獲取輸出數據中的力列,單位為牛,此處注釋中寫的'desired speed'應為筆誤,實際是力的意思
force = yout(:,5); % s, desired speed
% 創建新的圖形窗口
figure
% 將當前圖形窗口劃分為2行1列的子圖,選中第1個子圖
subplot(2,1,1)
% 繪制期望速度隨時間變化的曲線,設置線條屬性
plot(t,v_d,'r--','Linewidth',2);
% 保持當前圖形狀態
hold on
% 繪制實際速度隨時間變化的曲線,設置線條屬性
plot(t,v,'Linewidth',2);
% 設置x軸標簽
xlabel('Time (s)');
% 設置y軸標簽,單位為米每秒
ylabel('Speed (Mass/s)');
% 顯示網格
grid on
% 選中第2個子圖
subplot(2,1,2)
% 繪制期望速度隨時間變化的曲線(單位換算為千米每小時),設置線條屬性
plot(t,v_d/1000*3600,'r--','Linewidth',2);
% 保持當前圖形狀態
hold on
% 繪制實際速度隨時間變化的曲線(單位換算為千米每小時),設置線條屬性
plot(t,v/1000*3600,'Linewidth',2);
% 設置x軸標簽
xlabel('Time (s)');
% 設置y軸標簽,單位為千米每小時
ylabel('Speed (km/hr)');
% 顯示網格
grid on
% 添加圖例
legend('期望車速','實際車速')
% 創建新的圖形窗口
figure
% 將當前圖形窗口劃分為2行1列的子圖,選中第1個子圖
subplot(2,1,1)
% 繪制速度誤差隨時間變化的曲線,設置線條寬度
plot(t,v_tilde,'Linewidth',2);
% 設置x軸標簽
xlabel('Time (s)');
% 設置y軸標簽,單位為米每秒
ylabel('Error (Mass/s)');
% 顯示網格
grid on
% 選中第2個子圖
subplot(2,1,2)
% 繪制速度誤差隨時間變化的曲線(單位換算為千米每小時),設置線條寬度
plot(t,v_tilde/1000*3600,'Linewidth',2);
% 設置x軸標簽
xlabel('Time (s)');
% 設置y軸標簽,單位為千米每小時
ylabel('Error (km/hr)');
% 顯示網格
grid on
% 創建新的圖形窗口
figure
% 繪制力隨時間變化的曲線,設置線條寬度
plot(t,force,'Linewidth',2);
% 設置x軸標簽
xlabel('Time (s)');
% 設置y軸標簽,單位為牛
ylabel('Force (N)');
% 顯示網格
grid on
save R1.mat
4.系統原理簡介
車輛行駛控制系統旨在確保車輛在各種工況下能夠穩定、安全且高效地運行。隨著現代汽車技術的不斷發展,對于車輛行駛控制的精度和可靠性要求越來越高。基于空間狀態方程的控制方法為車輛行駛控制提供了一種系統且有效的手段,其中前饋控制和 PI 反饋控制是兩種重要的控制策略。前饋控制能夠根據系統的已知輸入預先計算出控制量,以補償可預見的干擾;而 PI 反饋控制則依據系統的誤差信號進行調節,以消除系統的穩態誤差并增強系統的穩定性。深入研究這兩種控制策略的原理對于提升車輛行駛控制系統的性能具有至關重要的意義。
前饋控制是一種開環控制策略,它基于對系統輸入和干擾的先驗知識,直接計算出所需的控制量,以抵消干擾對系統輸出的影響,從而使系統輸出能夠快速跟蹤期望輸出。在車輛行駛控制系統中,例如當我們知道車輛即將面臨一個特定的坡度變化或者風速變化等可預測的干擾時,前饋控制可以提前調整驅動力,以維持車輛速度的穩定。
PI 反饋控制由比例(P)控制和積分(I)控制兩部分組成。比例控制根據系統當前的誤差信號成比例地產生控制作用,能夠快速響應誤差的變化,但對于穩態誤差的消除能力有限。積分控制則對誤差信號進行積分,其輸出隨著時間的積累而不斷增大,直到系統的穩態誤差為零,從而能夠有效地消除穩態誤差,提高系統的控制精度。



 浙公網安備 33010602011771號
浙公網安備 33010602011771號